Input-file format

The input file consists of five parameter blocks named [model], [system], [impurity_solver], [control], and [tool].

The following table shows which blocks are used by each program.

	dcore_pre	dcore	dcore_check	dcore_post
[model]	Yes	Yes	Yes	Yes
[system]		Yes	Yes	Yes
[impurity_solver]		Yes		Yes
[control]		Yes
[tool]			Yes	Yes
[mpi]		Yes		Yes

For example, we can see that dcore_pre needs to be re-executed only when [model] block is changed.

The parameters included in each block are explained below.

[model] block

This block includes parameters for defining a model to be solved.

Name	Type	Default	Description
seedname	String	dcore	Name of the system. The model HDF5 file will be seedname.h5.
lattice	String	chain	Chosen from “chain”, “square”, “cubic”, “bethe”, “wannier90”, and “external”
t	Float	1.0	Transfer integral (Nearest neighbor)
t’	Float	0.0	Transfer integral (Second nearest)
nelec	Float	1.0	Number of electrons per unit cell.
norb	String	1	Number of orbitals at each correlated shell (ncor integers separated by commas or spaces.)
ncor	Integer	1	Number of correlated shells in a unit cell (for lattice = wannier90).
corr_to_inequiv	String	None	Mapping from correlated shells to equivalent shells (for lattice = wannier90)
bvec	String	[(1.0,0.0,0.0),(0.0,1.0,0.0),(0.0,0.0,1.0)]	Reciprocal lattice vectors in arbitrary unit.
nk	Integer	8	Number of k along each line
nk0	Integer	0	Number of k along b_0 (for lattice = wannier90, external)
nk1	Integer	0	Number of k along b_1 (for lattice = wannier90, external)
nk2	Integer	0	Number of k along b_2 (for lattice = wannier90, external)
spin_orbit	Bool	False	Whether the spin-orbit case.
interaction	String	kanamori	Chosen from “slater_uj”, “slater_f”, “kanamori”, “respack” (See below)
density_density	Bool	False	If true, only the density-density part of the interaction is used (See below).
kanamori	String	None	U (Diagonal Coulomb pot.), U’ (Off-diagonal Coulomb pot.) and J (Hund coupling) (See below).
slater_f	String	None	Angular momentum, Slater integrals F (See below).
slater_uj	String	None	Angular momentum, Slater integrals in U and J (See below).
local_potential_matrix	String	None	dict of {ish: ‘filename’} to specify local potential matrix of ish-th shell
local_potential_factor	String	1.0	Prefactors to the local potential matrix (float or list with len=ncor)

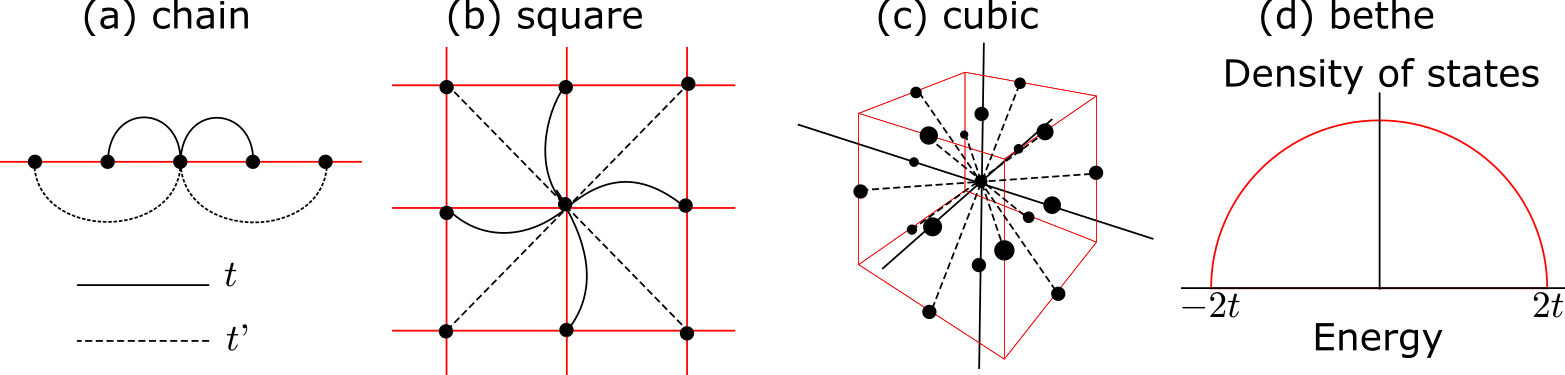
lattice

For model calculations, the following preset models are defined:

• chain

• square

• cubic

• bethe (semicircular DOS with energy ranges [-2t:2t])

For DFT+DMFT calculations, hopping parameters in the Wannier90 format can be imported by

• wannier90

  Place the Wannier90 file in the current directory with the name seedname_hr.dat.

For experts, the lattice data may be prepared by your own. In this case, use

• external

  In this mode, you should make all necessary data in dft_input group of seedname.h5. The data structure follows DFTTools. For details, see the reference manual of DFTTools.

  The pre-process dcore_pre does not touch the data in dft_input group, and write only additional data such as interactions into DCore group.

interaction

Model Hamiltonian is defined as

\[{\hat H} = \sum_{i j} \sum_{\alpha \beta}^{N_{\rm band}} \sum_{\sigma=\uparrow, \downarrow} t_{i \alpha j \beta} c_{i \alpha \sigma}^\dagger c_{j \beta \sigma} +h.c. + {\hat H}_{\rm int},\]

where

\[{\hat H}_{\rm int} = \frac{1}{2} \sum_{i, \alpha \beta \gamma \delta,\sigma \sigma'} U^{i}_{\alpha \beta \gamma \delta} c_{i \alpha \sigma}^\dagger c_{i \beta \sigma'}^\dagger c_{i \delta \sigma'} c_{i \gamma \sigma}.\]

The interaction matrix \(U^{i}_{\alpha \beta \gamma \delta}\) is specified by the parameter interaction.

• If interaction = kanamori

  In this case, the Kanamori-type interaction is used, i.e.

  \[\begin{split}\begin{align} U_{\alpha \alpha \alpha \alpha} &= U, \\ U_{\alpha \beta \alpha \beta} &= U' \qquad (\alpha \neq \beta), \\ U_{\alpha \beta \beta \alpha} &= J \qquad (\alpha \neq \beta), \\ U_{\alpha \alpha \beta \beta} &= J \qquad (\alpha \neq \beta), \end{align}\end{split}\]

  where \(U, U', J\) at each correlated shell are specified by the parameter kanamori as

  interaction = kanamori
  kanamori = [(U_1, U'_1, J_1), (U_2, U'_2, J_2), ... ]
  

  For example, if there are two correlated shells that have \((U, U', J) = (4, 2, 1)\) and \((U, U', J) = (6, 3, 1.5)\), respectively, you need to set the input parameters as

  interaction = kanamori
  kanamori = [(4.0, 2.0, 1.0), (6.0, 3.0, 1.5)]
  

• If interaction = slater_f

  In this case, the interaction matrix is constructed by the effective Slater integrals \(F_0, F_2, F_4, F_6\). These Slater integrals and the angular momentum at each correlated shell are specified by the parameter slater_f as follows

  interaction = slater_f
  slater_f = [(angular_momentum, F_0, F_2, F_4, F_6), ... ]
  

  For example, if there are two correlated shells, one has d-orbital with \((F_0, F_2, F_4) = (2, 1, 0.5)\) and the other has p-orbital with \((F_0, F_2) = (3, 1.5)\), you need to set the input parameter as

  interaction = slater_f
  slater_f = [(2, 2.0, 1.0, 0.5, 0.0), (1, 3.0, 1.5 0.0, 0.0)]
  

  Note

  You must specify all of \(F_0, F_2, F_4, F_6\).

• If interaction = slater_uj

  In this case, the Slater-type interaction is used. The effective Slater integrals are computed with the following formulae:

  • \(l = 1\)

    \[F_0 = U, \quad F_2 = 5 J\]

  • \(l=2\)

    \[F_0 = U, \quad F_2 = \frac{14 J}{1.0 + 0.63},\quad F_4 = 0.63 F_2\]

  • \(l=3\)

    \[F_0 = U, \quad F_2 = \frac{6435 J}{286 + 195 \times 451 / 675 + 250 \times 1001 / 2025},\quad F_4 = \frac{451 F_2}{675},\quad F_6 = \frac{1001 F_2}{2025}\]

  The \(U\), \(J\) and the angular momentum at each correlated shell are specified by the parameter slater_uj as

  interaction = slater_uj
  slater_uj = [(angular_momentum1, U1, J1), (angular_momentum2, U2, J2), ... ]
  

• If interaction = respack

  Use the output by RESPACK. Under construction.

If you want to treat only the density-density part

\[{\hat H}_{\rm int} = \frac{1}{2} \sum_{i, \alpha, \sigma \sigma'} U^{i}_{\alpha \alpha \alpha \alpha} c_{i \alpha \sigma}^\dagger c_{i \beta \sigma'}^\dagger c_{i \beta \sigma'} c_{i \alpha \sigma} + \frac{1}{2} \sum_{i, \alpha \neq \beta, \sigma \sigma'} U^{i}_{\alpha \beta \alpha \beta} c_{i \alpha \sigma}^\dagger c_{i \beta \sigma'}^\dagger c_{i \beta \sigma'} c_{i \alpha \sigma} + \frac{1}{2} \sum_{i, \alpha \neq \beta, \sigma} U^{i}_{\alpha \beta \beta \alpha} c_{i \alpha \sigma}^\dagger c_{i \beta \sigma}^\dagger c_{i \alpha \sigma} c_{i \beta \sigma},\]

you specify the parameter density_density as

density_density = True

Note

It can not be used in conjunction to the Hubbard-I solver or the double-counting correction.

local potential

An arbitrary local potential can be implemented using parameters local_potential_*. The format looks like

[model]
local_potential_matrix = {0: 'pot0.txt', 1: 'pot1.txt'}
local_potential_factor = 0.01

Here, local_potential_matrix describes, in the python dictionary format, a set of the inequivalent shell index ish and the filename which defines the local potential matrix. The parameter local_potential_factor defines a prefactor to the potential matrix.

For example, the Zeeman term along z-axis for S=1/2 is represented by

$ cat pot0.txt
# spin orb1 orb2  Re Im
0 0 0   0.5 0.
1 0 0  -0.5 0.

and the magnetic field is specified by local_potential_factor.

[system] block

This block includes thermodynamic parameters and some technical parameters such as the number of Matsubara frequencies.

Name	Type	Default	Description
beta	Float	1.0	Inverse temperature. This parameter is overridden, if T is given.
T	Float	-1.0	Temperature. If this parameter is given, beta is overridden by 1/T.
n_iw	Integer	2048	Number of Matsubara frequencies
fix_mu	Bool	False	Whether or not to fix chemical potential to a given value.
mu	Float	0.0	Initial chemical potential.
prec_mu	Float	0.0001	Threshold for calculating chemical potential with the bisection method.
with_dc	Bool	False	Whether or not use double-counting correction (See below)
dc_type	String	HF_DFT	Chosen from ‘HF_DFT’ (default), ‘HF_imp’, ‘FLL’

If the parameter with_dc is specified to True, the following part of the self-energy is subtracted to avoid the double-counting error of the self-energy.

\[\Sigma_{i, \alpha \sigma \beta \sigma'}^{\rm dc-imp} = \delta_{\sigma \sigma'} \sum_{\gamma \delta \sigma_1} U_{\alpha \gamma \beta \delta} \langle c_{\gamma \sigma_1}^\dagger c_{\delta \sigma_1}\rangle_0 - \sum_{\gamma \delta} U_{\alpha \gamma \delta \beta} \langle c_{\gamma \sigma'}^\dagger c_{\delta \sigma}\rangle_0,\]

where \(\langle \cdots \rangle_0\) indicates the expectation value at the initial (Kohn-Sham) state.

[impurity_solver] block

This block specifies an impurity solver to be used and necessary parameters for running the solver program.

Name	Type	Default	Description
name	String	null	Name of impurity solver. Available options are null, TRIQS/cthyb, TRIQS/hubbard-I, ALPS/cthyb, ALPS/cthyb-seg, pomerol.
basis_rotation	String	None	You can specify either ‘Hloc’, ‘None’, or the location of a file..

Additionally, we have to specify solver-dependent parameters in the way like n_cycles{int} = 500000. For details, see the reference manual for each solver.

[control] block

This block includes parameters that control the self-consistency loop of DMFT.

Name	Type	Default	Description
max_step	Integer	100	Maximum steps of DMFT loops
sigma_mix	Float	0.5	Mixing parameter for self-energy
restart	Bool	False	Whether or not restart from a previous calculation stored in a HDF file.
initial_static_self_energy	String	None	dict of {ish: ‘filename’} to specify initial value of the self-energy of ish-th shell. The file format is the same as local_potential_matrix.
initial_self_energy	String	None	Filename containing initial self-energy in the same format as sigma.dat generated by dcore_check.
time_reversal	Bool	False	If true, an average over spin components are taken.
symmetry_generators	String	None	Generators for symmetrization of self-energy.
n_converge	Integer	1	The DMFT loop is terminated if the convergence criterion defined with converge_tol is satisfied n_converge times consecutively.
converge_tol	Float	0.0	Tolerance in the convergence check. The chemical potential and the renormalization factor are examined.

[tool] block

This block includes parameters that are solely used by dcore_post.

Name	Type	Default	Description
nnode	Integer	0	[NOT USED] Number of node for the k path
nk_line	Integer	8	Number of k along each line
knode	String	[(G,0.0,0.0,0.0),(X,1.0,0.0,0.0)]	The name and the fractional coordinate of each k-node.
omega_min	Float	-1.0	Minimum value of real frequency
omega_max	Float	1.0	Max value of real frequency
Nomega	Integer	100	Number of real frequencies
broadening	Float	0.0	An additional Lorentzian broadening
eta	Float	0.0	Imaginary frequency shift for the Pade approximation
omega_pade	Float	1e+20	Cutoff frequency for the Pade approximation. Data in [-i omega_pade, i omega_pade] is used.
n_pade_min	Integer	20	Minimum number of Matsubara frequencies used for Pade approximation.
n_pade_max	Integer	-1	Maximum number of Matsubara frequencies used for Pade approximation. If negative, this will be replaced with n_iw in [system] block.
omega_check	Float	0.0	Maximum frequency for dcore_check. If not specified, a fixed number of Matsubara points are taken.
nk_mesh	Integer	0	Number of k points along each axis for computation of A(k,omega) on a 3D mesh
nk0_mesh	Integer	0	Number of k points along b_0 for computation of A(k,omega) on a 3D mesh
nk1_mesh	Integer	0	Number of k points along b_1 for computation of A(k,omega) on a 3D mesh
nk2_mesh	Integer	0	Number of k points along b_2 for computation of A(k,omega) on a 3D mesh

[mpi] block

This block includes parameters which are read by dcore and dcore_post.

Name	Type	Default	Description
command	String	mpirun -np #	Command for executing a MPI job. # will be relaced by the number of processes.

When an option -DMPIEXEC=<MPIRUN> is passed to the cmake command, The default value of command will be replaced with <MPIRUN>.