ファイルフォーマット

入力ファイル

ファイル名および計算条件指定ファイル

4つの namelist (filename, ham, cg, dyn)に分かれています. namelistのしくみについてはfortranについて書かれた書籍やWebページを参照してください.

&filename
  inham = ""
  invec = ""
/
&ham
nsite = 4
Jx = 1d0
Jy = 1d0
Jz = 1d0
Dz = 0d0
/
&cg
  maxloops = 100
  convfactor = 6
/
&dyn
  calctype = "normal"
  nomega = 100
  omegamin = (-2d0, 0.1d0)
  omegamax = ( 1d0, 0.1d0)
  outrestart = .TRUE.
/

"filename" ネームリストではハミルトニアンと右辺ベクトルを格納しているファイル名を指定します.

  • InHam

    形式 : string型 (default: "")

    説明 : MatrixMarket形式のハミルトニアンファイル名(フルパスもしくは相対パス)を指定します. これが指定されなかった場合には, ham ネームリストのパラメーターから1次元スピン系の ハミルトニアンが生成されます.

  • InVec

    形式 : string型 (default: "")

    説明 : 右辺ベクトルを格納したファイル名を指定します. これが指定されなかった場合には, まず最低エネルギー固有状態が計算され, それに \({\hat S}_{1 z}\) (サイト1のスピン:math:z 成分の演算子)がかかったものが右辺ベクトルとなります (すなわち1次元スピン系を計算しているものと勝手に解釈されます).

"ham" ネームリストはハミルトニアンが生成されるモードでのみ読み込まれ, 次のハミルトニアンで表される1次元スピン系(Fig. 2 ) を構成するパラメーターを指定することに使われます.

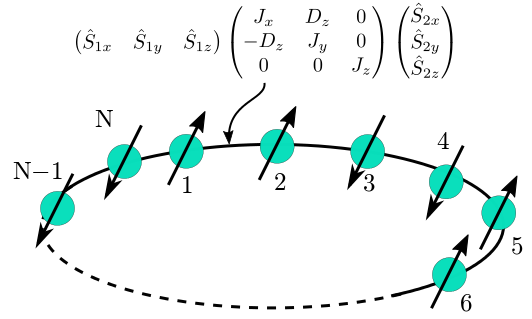
_images/spin.png

Figure 2: 1次元スピン系の模式図.

\[\begin{split}\begin{align} {\hat H} = \sum_{i} \left( \begin{matrix} {\hat S}_{i x} & {\hat S}_{i y} & {\hat S}_{i z} \end{matrix} \right) \left( \begin{matrix} J_x & D_z & 0 \\ -D_z & J_y & 0 \\ 0 & 0 & J_z \end{matrix} \right) \left( \begin{matrix} {\hat S}_{i+1 x} \ {\hat S}_{i+1 y} \ {\hat S}_{i+1 z} \end{matrix} \right)\end{align}\end{split}\]

  • nsite

    形式 : 整数 (default: 4)

    説明 : 1次元スピン模型のサイト数を指定します.

  • Jx

    形式 : 実数 (default: 1.0)

    説明 : Heisenberg模型の \(J_x\) を指定します.

  • Jy

    形式 : 実数 (default: 1.0)

    説明 : Heisenberg模型の \(J_y\) を指定します.

  • Jz

    形式 : 実数 (default: 1.0)

    説明 : Heisenberg模型の \(J_z\) を指定します.

  • Dz

    形式 : 実数 (default: 0.0)

    説明 : Dzyaloshinskii-Moriya相互作用のパラメーター \(D_z\) を指定します.

cg ネームリストでは(双)共役勾配法の反復に関するパラメーターを指定します.

  • MaxLoops

    形式 : 整数 (default: ハミルトニアンの次元)

    説明 : 最大反復回数を指定します.

  • Convfactor

    形式 : 整数 (default: 8)

    説明 : 残差ベクトルの二乗ノルムを次元数で割ったものが, \(10^{-{\tt Convfactor}}\) 未満となったら収束したとみなして計算を終了します.

dyn ネームリストではスペクトルの計算に関するパラメーターを指定します.

  • OmegaMin

    形式 : 複素数 (default: invec を指定しなかった場合には (ハミルトニアンの最小固有値, 最大 \(\cdot\) 最小固有値の差 \(\times0.01\)), それ以外の場合には (0.0, 0.01))

    説明 : 振動数の始点を指定します.

  • OmegaMax

    形式 : 複素数 (default: invec を指定しなかった場合には (ハミルトニアンの最大固有値, 最大 \(\cdot\) 最小固有値の差 \(\times0.01\)), それ以外の場合には (1.0, 0.01))

    説明 : 振動数の終点を指定します.

  • NOmega

    形式 : 整数 (default: 10)

    説明 : 振動数の点数を指定します.

  • outrestart

    形式 : 論理型 (default: .FALSE.)

    説明 : リスタート用ファイルを出力するか( .TRUE.)否か( .FALSE.)を指定します.

  • calctype

    形式 : String型. "normal", "recalc", "restart" のいずれか. (default: "normal")

    説明 : "normal" が指定された場合にはKrylov部分空間法をはじめから行います. "recalc" の場合には先行する計算で出力されたリスタート用ファイルを読み込み 先行する計算で行われたのと同じ反復回数まで計算します. 収束は保証されません. "restart" では先行する計算で出力されたリスタート用ファイルを読み込み, 先行する計算で行われたのと同じ反復回数まで計算したのち, 収束するか最大反復回数( MaxLoops)に達するまで計算を続けます.

InHamファイル

MatrixMarket形式に準じ, 以下のフォーマットを採用しています.

InHamファイルの例

%%MatrixMarket matrix coordinate complex hermitian
16 16 20
1 1 1.000000 0.000000
3 2 0.500000 0.000000
5 3 0.500000 0.000000
6 4 0.500000 0.000000
6 6 -1.000000 0.000000
7 6 0.500000 0.000000
9 2 0.500000 0.000000
9 5 0.500000 0.000000
10 6 0.500000 0.000000
11 4 0.500000 0.000000
11 7 0.500000 0.000000
11 10 0.500000 0.000000
11 11 -1.000000 0.000000
12 8 0.500000 0.000000
13 6 0.500000 0.000000
13 11 0.500000 0.000000
14 12 0.500000 0.000000
15 8 0.500000 0.000000
15 14 0.500000 0.000000
16 16 1.000000 0.000000
1行目:

任意の文字列(コメントなど)が入ります.

2行目:

行数, 列数, 非ゼロ要素の数が入ります. 非ゼロ要素数に関しては 行列の下三角部分のみ の数を記入してください.

3行目以降:

行番号, 列番号, 要素の実部, 要素の虚部が入ります. 2行目で入れた, 非ゼロ要素数と同じ数(下三角部分のみ)記入してください.

InVecファイル

励起ベクトルを入力するテキスト形式のファイルです. ファイル名は入出力ファイル指定ファイルで指定します. 以下のようなフォーマットをしています.

8192
0.02 0.01
0.02 0.001
(continue...)

  • 1行目: [ int01 ]

    形式 : int型

    説明 : 計算対象のヒルベルト空間数を指定する整数. ハミルトニアンの次元と一致している必要があります.

  • 2行目-: [ double01 ] [ double02 ]

    形式 : double型

    説明 : 励起ベクトルの値を表します. [ double01 ] が実部, [ double02 ] が虚部を表します.

リスタート用係数

リスタート用の係数を入力するテキスト形式のファイルです. ファイル名は TriDiagComp.dat です. 以下のようなフォーマットをしています.

1000
1.0 0.0
0.1 0 0.01  0
0.2 0 0.021 0
(continue...)
2.1 -0.5
3.1 4.0
(continue...)

  • 1行目: [ int01 ]

    形式 : int型

    説明 : \(\alpha, \beta\) の読み込み総数を表します. 前回計算時のイタレーション数に相当します.

  • 2行目: [ double01 ] [ double02 ]

    形式 : double型

    説明 : シード振動数 \(z_{\rm seed}\) の値を表します. [ double01 ] が \(z_{\rm seed}\) の実部, [ double02 ] が \(z_{\rm seed}\) の虚部を表します.

  • 3行目-2+ [ int01 ] 行目: [ double03 ] [ double04 ] [ double05 ] [ double06 ]

    形式 : double型

    説明 : \(\alpha, \beta\) の値を表します. [ double03 ] が \(\alpha\) の実部, [ double04 ] が \(\alpha\) の虚部, [ double05 ] が \(\beta\) の実部, [ double06 ] が \(\beta\) の虚部を表します.

  • 3+ [ int01 ] 行目-2 + 2 \(\times\) [ int01 ] 行目: [ double07 ] [ double08 ]

    形式 : double型

    説明 : 各反復での残差ベクトルと励起ベクトルの内積を表します. [ double07 ] が実部, [ double08 ] が虚部を表します.

リスタート用ベクトル

リスタート用ベクトルを入力するテキスト形式のファイルです. ファイル名は ResVec.dat です. 以下のようなフォーマットをしています.

8192
0.02 0.01
0.02 0.001
(continue...)
0.02 0.01
0.02 0.001
(continue... Only for BiCG)

  • 1行目: [ int01 ]

    形式 : int型

    説明 : 計算対象のヒルベルト空間数を指定する整数.

  • 2行目-1+ [ int01 ] 行目: [ double01 ] [ double02 ]

    形式 : double型

    説明 : 残差ベクトルの値を表します. [ double01 ] が実部, [ double02 ] が虚部を表します.

  • 3行目-1+ \(2\times[\) int01 ] 行目: [ double03 ] [ double04 ]

    形式 : double型

    説明 : (ハミルトニアンが複素の場合のみ出力)影の残差ベクトルの値を表します. [ double03 ] が実部, [ double04 ] が虚部を表します.

出力ファイル

リスタート用係数

Sec. リスタート用係数 と同じ形式を取ります.

リスタート用ベクトル

Sec. リスタート用ベクトル と同じ形式を取ります.

動的グリーン関数ファイル

動的グリーン関数の計算結果を出力するテキスト形式のファイルです. 以下のようなフォーマットをしています.

-10 0.001 0.001 -0.0001
-9.8 0.001 0.0012 -0.0002
-9.6 0.001 0.0014 -0.0003
(continue...)

  • 1行目-: [ double01 ] [ double02 ] [ double03 ] [ double04 ]

    • [ double01 ], [ double02 ]

      形式 : double型

      説明 : 周波数数の実部 [ double01 ] と虚部 [ double02 ] を表します.

    • [ double03 ], [ double04 ]

      形式 : double型

      説明 : 動的グリーン関数の値を表します. [ double01 ] が実部, [ double02 ] が虚部を表します.