Tutorial

In this tutorial, we explain through a sample calculation of the 8-site Hubbard model on the square lattice.

Run HPhi/vmc.out

• For \({\mathcal H}\Phi\)

  We calculate the ground state and the correlation function with the following input file

  a0w = 2
  a0l = 2
  a1w = -2
  a1l = 2
  model="Hubbard"
  method="CG"
  lattice="square"
  t=1.0
  U=8.0
  ncond = 8
  2Sz=0
  

  $ HPhi -s input
  

• For mVMC

  First, we optimize the trial wavefunction with the following input

  a0w = 2
  a0l = 2
  a1w = -2
  a1l = 2
  model="Hubbard"
  lattice="square"
  t=1.0
  U=8.0
  ncond = 8
  2Sz=0
  

  $ vmc.out -s input
  

  We add the following line to the input file to compute the correlation function.

  NVMCCalMode = 1
  

  Compute the correlation function.

  $ vmc.out -s input output/zqp_opt.dat
  

Then the one- and two-body correlation function are written to files in the output/ directory.

Related files

• StdFace.def (See the manuals for mVMC/\({\mathcal H}\Phi\))

• zqp_opt.dat (See the manual for mVMC)

• greenone.def (Specify the index of correlation function to be computed)

• greentwo.def (Specify the index of correlation function to be computed)

Fourier transformation of correlation functions

Perform the Fourier transformation of the correlation function by using the utility greenr2k.

$ echo "4 20
G 0 0 0
X 0.5 0 0
M 0.5 0.5 0
G 0 0 0
16 16 1" >> geometry.dat
$ greenr2k namelist.def geometry.dat

Then the Fourier-transformed correlation functions are written to a file in output/.

Related files

• output/zvo_cisajs_001.dat (Results of correlation function in the site representation)

• output/zvo_cisajs.dat (Results of correlation function in the site representation)

• output/zvo_cisajscktalt_001.dat (Results of correlation function in the site representation)

• output/zvo_cisajscktalt.dat (Results of correlation function in the site representation)

• geometry.dat (Geometry)

• output/zvo_corr.dat (Correlation functions on the k path)

Display correlation functions

Plot the correlation function in the k space by using gnuplot.

load "kpath.gp"
plot "output/zvo_corr_eigen0.dat" u 1:12 w l

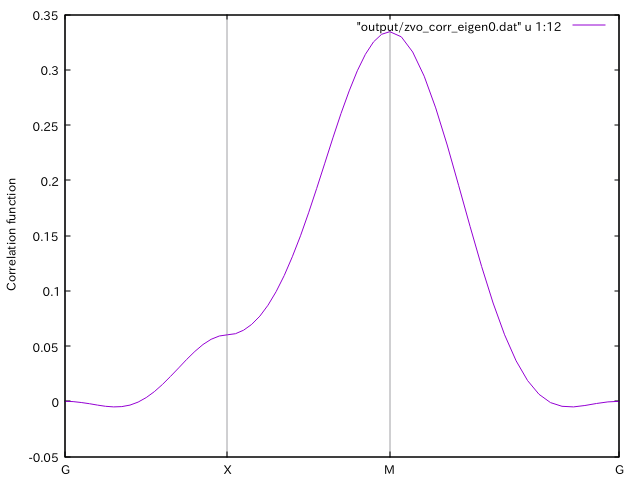
Figure 1: The spin-spin correlation \(\langle{\bf S}_{\bf k}\cdot{\bf S}_{\bf k}\rangle\) (Column 12).

Related files

• kpath.gp (gnuplot script)

• output/zvo_corr.dat (Correlation functions on the k path)