HΦ  3.2.0
Functions
Lanczos_EigenValue.c File Reference

Calculate eigenvalues by the Lanczos method. More...

#include "Common.h"
#include "common/setmemory.h"
#include "mltply.h"
#include "vec12.h"
#include "bisec.h"
#include "FileIO.h"
#include "matrixlapack.h"
#include "Lanczos_EigenValue.h"
#include "wrapperMPI.h"
#include "CalcTime.h"
+ Include dependency graph for Lanczos_EigenValue.c:

Go to the source code of this file.

Functions

int Lanczos_EigenValue (struct BindStruct *X)
 Main function for calculating eigen values by Lanczos method.
The energy convergence is judged by the level of target energy determined by \( \verb|k_exct| \).
. More...
 
int Lanczos_GetTridiagonalMatrixComponents (struct BindStruct *X, double *_alpha, double *_beta, double complex *tmp_v1, unsigned long int *liLanczos_step)
 Calculate tridiagonal matrix components by Lanczos method. More...
 
int ReadInitialVector (struct BindStruct *X, double complex *_v0, double complex *_v1, unsigned long int *liLanczosStp_vec)
 Read initial vectors for the restart calculation. More...
 
int OutputLanczosVector (struct BindStruct *X, double complex *tmp_v0, double complex *tmp_v1, unsigned long int liLanczosStp_vec)
 Output initial vectors for the restart calculation. More...
 
void SetInitialVector (struct BindStruct *X, double complex *tmp_v0, double complex *tmp_v1)
 Set initial vector to start the calculation for Lanczos method.
. More...
 
int ReadTMComponents (struct BindStruct *X, double *_dnorm, unsigned long int *_i_max, int iFlg)
 Read tridiagonal matrix components obtained by the Lanczos method.
. More...
 
int OutputTMComponents (struct BindStruct *X, double *_alpha, double *_beta, double _dnorm, int liLanczosStp)
 Output tridiagonal matrix components obtained by the Lanczos method. More...
 

Detailed Description

Calculate eigenvalues by the Lanczos method.

Version
0.1
Author
Takahiro Misawa (The University of Tokyo)
Kazuyoshi Yoshimi (The University of Tokyo)

Definition in file Lanczos_EigenValue.c.

Function Documentation

◆ Lanczos_EigenValue()

int Lanczos_EigenValue ( struct BindStruct *  X)

Main function for calculating eigen values by Lanczos method.
The energy convergence is judged by the level of target energy determined by \( \verb|k_exct| \).
.

Parameters
X[in] Struct to give the information for calculating the eigen values.
Return values
-2Fail to read the initial vectors or triangular matrix components.
-1Fail to obtain the eigen values with in the \( \verb| Lanczos_max |\) step
0Succeed to calculate the eigen values.
Version
0.1
Author
Takahiro Misawa (The University of Tokyo)
Kazuyoshi Yoshimi (The University of Tokyo)

Definition at line 50 of file Lanczos_EigenValue.c.

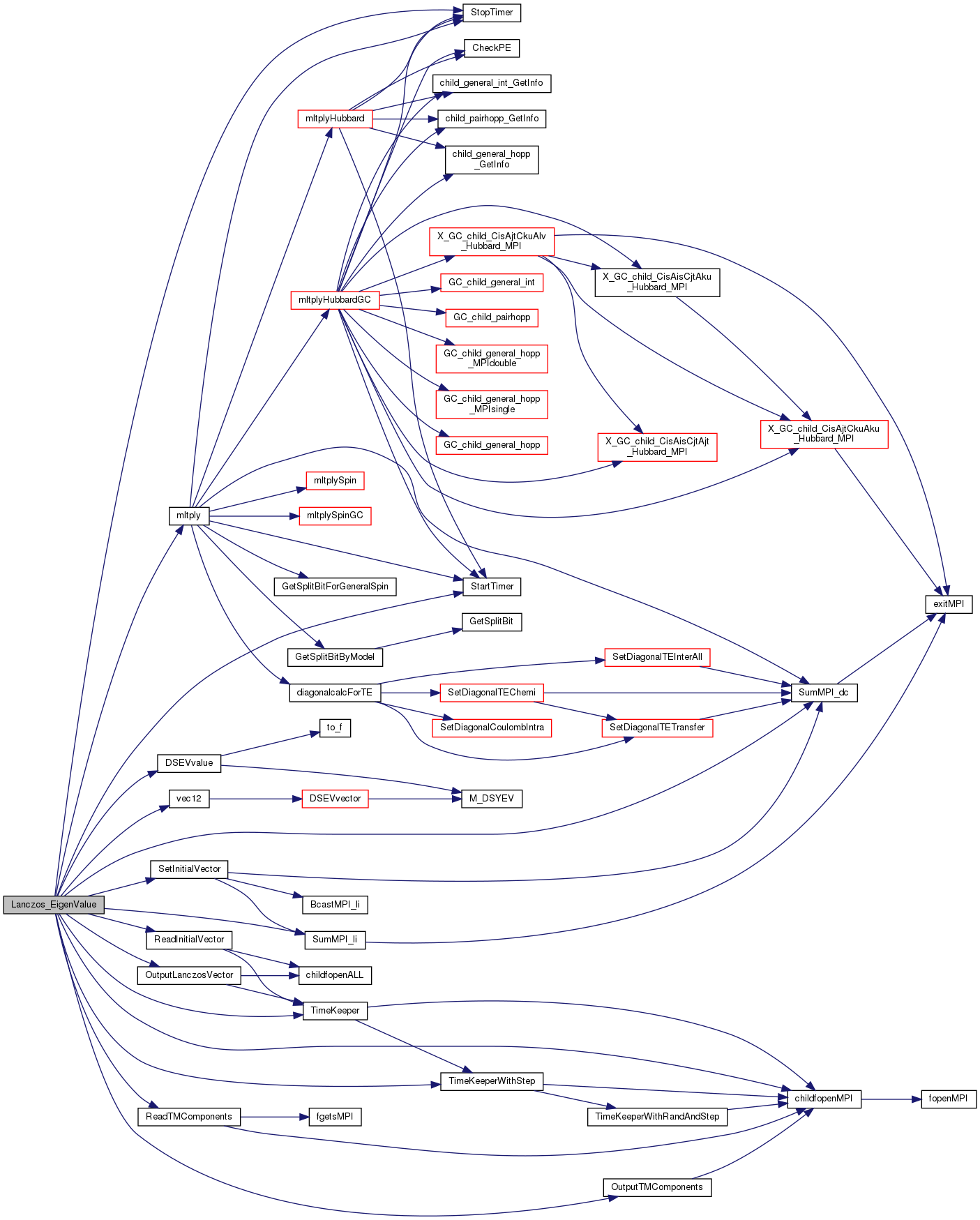
References alpha, beta, DefineList::CDataFileHead, cFileNameLanczosStep, cFileNameTimeKeep, BindStruct::Check, childfopenMPI(), cLanczos_EigenValueFinish, cLanczos_EigenValueStart, cLanczos_EigenValueStep, cLogLanczos_EigenValueEnd, cLogLanczos_EigenValueNotConverged, cLogLanczos_EigenValueStart, D_FileNameMax, BindStruct::Def, DSEVvalue(), eps_Lanczos, CheckList::idim_max, DefineList::iReStart, LargeList::itr, DefineList::k_exct, DefineList::Lanczos_max, DefineList::Lanczos_restart, DefineList::LanczosTarget, BindStruct::Large, mfint, mltply(), DefineList::NsiteMPI, OutputLanczosVector(), OutputTMComponents(), BindStruct::Phys, LargeList::prdct, ReadInitialVector(), ReadTMComponents(), SetInitialVector(), StartTimer(), stdoutMPI, StopTimer(), SumMPI_dc(), SumMPI_li(), PhysList::Target_CG_energy, PhysList::Target_energy, TimeKeeper(), TimeKeeperWithStep(), TRUE, v0, v1, and vec12().

Referenced by CalcByLanczos().

50  {
51 
52  fprintf(stdoutMPI, "%s", cLogLanczos_EigenValueStart);
53  FILE *fp;
54  char sdt[D_FileNameMax], sdt_2[D_FileNameMax];
55  int stp;
56  long int i, i_max;
57  unsigned long int i_max_tmp;
58  int k_exct, Target;
59  int iconv = -1;
60  double beta1, alpha1; //beta,alpha1 should be real
61  double complex temp1, temp2;
62  double complex cbeta1;
63  double E[5], ebefor, E_target;
64 
65 // for GC
66  double dnorm=0.0;
67 
68  double **tmp_mat;
69  double *tmp_E;
70  int int_i, int_j, mfint[7];
71  int iret=0;
72  sprintf(sdt_2, cFileNameLanczosStep, X->Def.CDataFileHead);
73 
74  i_max = X->Check.idim_max;
75  k_exct = X->Def.k_exct;
76  unsigned long int liLanczosStp;
77  liLanczosStp = X->Def.Lanczos_max;
78  unsigned long int liLanczosStp_vec=0;
79 
80  if (X->Def.iReStart == RESTART_INOUT || X->Def.iReStart == RESTART_IN){
81  if(ReadInitialVector( X, v0, v1, &liLanczosStp_vec)!=0){
82  fprintf(stdoutMPI, " Error: Fail to read initial vectors\n");
83  return -2;
84  }
85  iret=ReadTMComponents(X, &dnorm, &liLanczosStp, 0);
86  if(iret !=TRUE){
87  fprintf(stdoutMPI, " Error: Fail to read TMcomponents\n");
88  return -2;
89  }
90  if(liLanczosStp_vec !=liLanczosStp){
91  fprintf(stdoutMPI, " Error: Input files for vector and TMcomponents are incoorect.\n");
92  fprintf(stdoutMPI, " Error: Input vector %ld th stps, TMcomponents %ld th stps.\n", liLanczosStp_vec, liLanczosStp);
93  return -2;
94  }
95  X->Def.Lanczos_restart=liLanczosStp;
96  //Calculate EigenValue
97 
98  liLanczosStp = liLanczosStp+X->Def.Lanczos_max;
99  alpha1=alpha[X->Def.Lanczos_restart];
100  beta1=beta[X->Def.Lanczos_restart];
101  }/*X->Def.iReStart == RESTART_INOUT || X->Def.iReStart == RESTART_IN*/
102  else {
103  SetInitialVector(X, v0, v1);
104  //Eigenvalues by Lanczos method
105  TimeKeeper(X, cFileNameTimeKeep, cLanczos_EigenValueStart, "a");
106  StartTimer(4101);
107  mltply(X, v0, v1);
108  StopTimer(4101);
109  stp = 1;
110  TimeKeeperWithStep(X, cFileNameTimeKeep, cLanczos_EigenValueStep, "a", stp);
111 
112  alpha1 = creal(X->Large.prdct);// alpha = v^{\dag}*H*v
113 
114  alpha[1] = alpha1;
115  cbeta1 = 0.0;
116 
117 #pragma omp parallel for reduction(+:cbeta1) default(none) private(i) shared(v0, v1) firstprivate(i_max, alpha1)
118  for (i = 1; i <= i_max; i++) {
119  cbeta1 += conj(v0[i] - alpha1 * v1[i]) * (v0[i] - alpha1 * v1[i]);
120  }
121  cbeta1 = SumMPI_dc(cbeta1);
122  beta1 = creal(cbeta1);
123  beta1 = sqrt(beta1);
124  beta[1] = beta1;
125  ebefor = 0;
126  liLanczosStp = X->Def.Lanczos_max;
127  X->Def.Lanczos_restart =1;
128  }/*else restart*/
129 
130  /*
131  * Set Maximum number of loop to the dimention of the Wavefunction
132  */
133  i_max_tmp = SumMPI_li(i_max);
134  if (i_max_tmp < liLanczosStp) {
135  liLanczosStp = i_max_tmp;
136  }
137  if (i_max_tmp < X->Def.LanczosTarget) {
138  liLanczosStp = i_max_tmp;
139  }
140  if (i_max_tmp == 1) {
141  E[1] = alpha[1];
142  StartTimer(4102);
143  vec12(alpha, beta, stp, E, X);
144  StopTimer(4102);
145  X->Large.itr = stp;
146  X->Phys.Target_energy = E[k_exct];
147  iconv = 0;
148  fprintf(stdoutMPI, " LanczosStep E[1] \n");
149  fprintf(stdoutMPI, " stp=%d %.10lf \n", stp, E[1]);
150  }
151 
152  fprintf(stdoutMPI, " LanczosStep E[1] E[2] E[3] E[4] Target:E[%d] E_Max/Nsite\n", X->Def.LanczosTarget + 1);
153  for (stp = X->Def.Lanczos_restart+1; stp <= liLanczosStp; stp++) {
154 #pragma omp parallel for default(none) private(i,temp1, temp2) shared(v0, v1) firstprivate(i_max, alpha1, beta1)
155  for (i = 1; i <= i_max; i++) {
156  temp1 = v1[i];
157  temp2 = (v0[i] - alpha1 * v1[i]) / beta1;
158  v0[i] = -beta1 * temp1;
159  v1[i] = temp2;
160  }
161 
162  StartTimer(4101);
163  mltply(X, v0, v1);
164  StopTimer(4101);
165  TimeKeeperWithStep(X, cFileNameTimeKeep, cLanczos_EigenValueStep, "a", stp);
166  alpha1 = creal(X->Large.prdct);
167  alpha[stp] = alpha1;
168  cbeta1 = 0.0;
169 
170 #pragma omp parallel for reduction(+:cbeta1) default(none) private(i) shared(v0, v1) firstprivate(i_max, alpha1)
171  for (i = 1; i <= i_max; i++) {
172  cbeta1 += conj(v0[i] - alpha1 * v1[i]) * (v0[i] - alpha1 * v1[i]);
173  }
174  cbeta1 = SumMPI_dc(cbeta1);
175  beta1 = creal(cbeta1);
176  beta1 = sqrt(beta1);
177  beta[stp] = beta1;
178 
179  Target = X->Def.LanczosTarget;
180 
181  if (stp == 2) {
182  tmp_mat = d_2d_allocate(stp,stp);
183  tmp_E = d_1d_allocate(stp+1);
184 
185  for (int_i = 0; int_i < stp; int_i++) {
186  for (int_j = 0; int_j < stp; int_j++) {
187  tmp_mat[int_i][int_j] = 0.0;
188  }
189  }
190  tmp_mat[0][0] = alpha[1];
191  tmp_mat[0][1] = beta[1];
192  tmp_mat[1][0] = beta[1];
193  tmp_mat[1][1] = alpha[2];
194  DSEVvalue(stp, tmp_mat, tmp_E);
195  E[1] = tmp_E[0];
196  E[2] = tmp_E[1];
197  if (Target < 2) {
198  E_target = tmp_E[Target];
199  ebefor = E_target;
200  }
201  free_d_1d_allocate(tmp_E);
202  free_d_2d_allocate(tmp_mat);
203 
204  childfopenMPI(sdt_2, "w", &fp);
205 
206  fprintf(fp, "LanczosStep E[1] E[2] E[3] E[4] Target:E[%d] E_Max/Nsite\n", Target + 1);
207  if (Target < 2) {
208  fprintf(stdoutMPI, " stp = %d %.10lf %.10lf xxxxxxxxxx xxxxxxxxx %.10lf xxxxxxxxx \n", stp, E[1], E[2],
209  E_target);
210  fprintf(fp, "stp = %d %.10lf %.10lf xxxxxxxxxx xxxxxxxxx %.10lf xxxxxxxxx \n", stp, E[1], E[2], E_target);
211  } else {
212  fprintf(stdoutMPI, " stp = %d %.10lf %.10lf xxxxxxxxxx xxxxxxxxx xxxxxxxxx xxxxxxxxx \n", stp, E[1], E[2]);
213  fprintf(fp, "stp = %d %.10lf %.10lf xxxxxxxxxx xxxxxxxxx xxxxxxxxx xxxxxxxxx \n", stp, E[1], E[2]);
214  }
215 
216  fclose(fp);
217  }
218 
219  //if (stp > 2 && stp % 2 == 0) {
220  if (stp > 2) {
221  childfopenMPI(sdt_2, "a", &fp);
222  tmp_mat = d_2d_allocate(stp,stp);
223  tmp_E = d_1d_allocate(stp+1);
224 
225  for (int_i = 0; int_i < stp; int_i++) {
226  for (int_j = 0; int_j < stp; int_j++) {
227  tmp_mat[int_i][int_j] = 0.0;
228  }
229  }
230  tmp_mat[0][0] = alpha[1];
231  tmp_mat[0][1] = beta[1];
232  for (int_i = 1; int_i < stp - 1; int_i++) {
233  tmp_mat[int_i][int_i] = alpha[int_i + 1];
234  tmp_mat[int_i][int_i + 1] = beta[int_i + 1];
235  tmp_mat[int_i][int_i - 1] = beta[int_i];
236  }
237  tmp_mat[int_i][int_i] = alpha[int_i + 1];
238  tmp_mat[int_i][int_i - 1] = beta[int_i];
239  StartTimer(4103);
240  DSEVvalue(stp, tmp_mat, tmp_E);
241  StopTimer(4103);
242  E[1] = tmp_E[0];
243  E[2] = tmp_E[1];
244  E[3] = tmp_E[2];
245  E[4] = tmp_E[3];
246  E[0] = tmp_E[stp - 1];
247  if (stp > Target) {
248  E_target = tmp_E[Target];
249  }
250  free_d_1d_allocate(tmp_E);
251  free_d_2d_allocate(tmp_mat);
252  if (stp > Target) {
253  fprintf(stdoutMPI, " stp = %d %.10lf %.10lf %.10lf %.10lf %.10lf %.10lf\n", stp, E[1], E[2], E[3], E[4],
254  E_target, E[0] / (double) X->Def.NsiteMPI);
255  fprintf(fp, "stp=%d %.10lf %.10lf %.10lf %.10lf %.10lf %.10lf\n", stp, E[1], E[2], E[3], E[4], E_target,
256  E[0] / (double) X->Def.NsiteMPI);
257  } else {
258  fprintf(stdoutMPI, " stp = %d %.10lf %.10lf %.10lf %.10lf xxxxxxxxx %.10lf\n", stp, E[1], E[2], E[3], E[4],
259  E[0] / (double) X->Def.NsiteMPI);
260  fprintf(fp, "stp=%d %.10lf %.10lf %.10lf %.10lf xxxxxxxxx %.10lf\n", stp, E[1], E[2], E[3], E[4],
261  E[0] / (double) X->Def.NsiteMPI);
262  }
263  fclose(fp);
264  if (stp > Target) {
265  if (fabs((E_target - ebefor) / E_target) < eps_Lanczos || fabs(beta[stp]) < pow(10.0, -14)) {
266  /*
267  if(X->Def.iReStart == RESTART_INOUT ||X->Def.iReStart == RESTART_OUT){
268  break;
269  }
270  */
271  tmp_E = d_1d_allocate(stp+1);
272  StartTimer(4102);
273  vec12(alpha, beta, stp, tmp_E, X);
274  StopTimer(4102);
275  X->Large.itr = stp;
276  X->Phys.Target_energy = E_target;
277  X->Phys.Target_CG_energy = tmp_E[k_exct]; //for CG
278  iconv = 0;
279  free_d_1d_allocate(tmp_E);
280  break;
281  }
282  ebefor = E_target;
283  }
284 
285  }
286  }
287  if (X->Def.iReStart == RESTART_INOUT ||X->Def.iReStart == RESTART_OUT ){
288  if(stp != X->Def.Lanczos_restart+2) { // 2 steps are needed to get the value: E[stp+2]-E[stp+1]
289  OutputTMComponents(X, alpha, beta, dnorm, stp - 1);
290  OutputLanczosVector(X, v0, v1, stp - 1);
291  }
292  if (iconv !=0){
293  sprintf(sdt, "%s", cLogLanczos_EigenValueNotConverged);
294  fprintf(stdoutMPI, "Lanczos Eigenvalue is not converged in this process (restart mode).\n");
295  return 1;
296  }
297  }
298 
299  sprintf(sdt, cFileNameTimeKeep, X->Def.CDataFileHead);
300  if (iconv != 0) {
301  sprintf(sdt, "%s", cLogLanczos_EigenValueNotConverged);
302  fprintf(stdoutMPI, "Lanczos Eigenvalue is not converged in this process.\n");
303  return -1;
304  }
305 
306  TimeKeeper(X, cFileNameTimeKeep, cLanczos_EigenValueFinish, "a");
307  fprintf(stdoutMPI, "%s", cLogLanczos_EigenValueEnd);
308 
309  return 0;
310 }
BindStruct::Def
struct DefineList Def
Definision of system (Hamiltonian) etc.
Definition: struct.h:410
mltply
int mltply(struct BindStruct *X, double complex *tmp_v0, double complex *tmp_v1)
Parent function of multiplying the wavefunction by the Hamiltonian. . First, the calculation of diago...
Definition: mltply.c:56
StartTimer
void StartTimer(int n)
function for initializing elapse time [start]
Definition: time.c:71
SumMPI_dc
double complex SumMPI_dc(double complex norm)
MPI wrapper function to obtain sum of Double complex across processes.
Definition: wrapperMPI.c:205
LargeList::itr
int itr
Iteration number.
Definition: struct.h:315
CheckList::idim_max
unsigned long int idim_max
The dimension of the Hilbert space of this process.
Definition: struct.h:303
DefineList::iReStart
int iReStart
Definition: struct.h:221
cLogLanczos_EigenValueNotConverged
const char * cLogLanczos_EigenValueNotConverged
Definition: LogMessage.c:89
PhysList::Target_CG_energy
double Target_CG_energy
Taget energy of CG-inversed iteration (NOT LOBCG) method.
Definition: struct.h:389
SetInitialVector
void SetInitialVector(struct BindStruct *X, double complex *tmp_v0, double complex *tmp_v1)
Set initial vector to start the calculation for Lanczos method. .
Definition: Lanczos_EigenValue.c:499
StopTimer
void StopTimer(int n)
function for calculating elapse time [elapse time=StartTimer-StopTimer]
Definition: time.c:83
v1
double complex * v1
Definition: global.h:35
LargeList::prdct
double complex prdct
The expectation value of the energy.
Definition: struct.h:314
D_FileNameMax
#define D_FileNameMax
Definition: global.h:23
BindStruct::Large
struct LargeList Large
Variables for Matrix-Vector product.
Definition: struct.h:412
childfopenMPI
int childfopenMPI(const char *_cPathChild, const char *_cmode, FILE **_fp)
Only the root process open file in output/ directory.
Definition: FileIO.c:27
cLanczos_EigenValueFinish
const char * cLanczos_EigenValueFinish
Definition: LogMessage.c:93
BindStruct::Phys
struct PhysList Phys
Physical quantities.
Definition: struct.h:413
DSEVvalue
int DSEVvalue(int xNsize, double **A, double *r)
obtain eigenvalues of real symmetric A
Definition: matrixlapack.c:93
cFileNameLanczosStep
const char * cFileNameLanczosStep
Definition: global.c:39
TRUE
#define TRUE
Definition: global.h:26
OutputLanczosVector
int OutputLanczosVector(struct BindStruct *X, double complex *tmp_v0, double complex *tmp_v1, unsigned long int liLanczosStp_vec)
Output initial vectors for the restart calculation.
Definition: Lanczos_EigenValue.c:466
DefineList::Lanczos_restart
int Lanczos_restart
Number of iterations performed in the restart computation.
Definition: struct.h:75
cLogLanczos_EigenValueStart
const char * cLogLanczos_EigenValueStart
Definition: ProgressMessage.c:36
cLogLanczos_EigenValueEnd
const char * cLogLanczos_EigenValueEnd
Definition: ProgressMessage.c:37
cLanczos_EigenValueStart
const char * cLanczos_EigenValueStart
Definition: LogMessage.c:91
mfint
static unsigned long int mfint[7]
Definition: xsetmem.c:33
ReadInitialVector
int ReadInitialVector(struct BindStruct *X, double complex *_v0, double complex *_v1, unsigned long int *liLanczosStp_vec)
Read initial vectors for the restart calculation.
Definition: Lanczos_EigenValue.c:428
DefineList::NsiteMPI
unsigned int NsiteMPI
Total number of sites, differ from DefineList::Nsite.
Definition: struct.h:57
alpha
double * alpha
Definition: global.h:44
cFileNameTimeKeep
const char * cFileNameTimeKeep
Definition: global.c:23
beta
double * beta
Definition: global.h:44
vec12
void vec12(double alpha[], double beta[], unsigned int ndim, double tmp_E[], struct BindStruct *X)
Diagonalize a tri-diagonal matrix and store eigenvectors into vec.
Definition: vec12.c:31
OutputTMComponents
int OutputTMComponents(struct BindStruct *X, double *_alpha, double *_beta, double _dnorm, int liLanczosStp)
Output tridiagonal matrix components obtained by the Lanczos method.
Definition: Lanczos_EigenValue.c:697
cLanczos_EigenValueStep
const char * cLanczos_EigenValueStep
Definition: LogMessage.c:92
DefineList::LanczosTarget
int LanczosTarget
Which eigenstate is used to check convergence. Read from Calcmod in readdef.h.
Definition: struct.h:50
ReadTMComponents
int ReadTMComponents(struct BindStruct *X, double *_dnorm, unsigned long int *_i_max, int iFlg)
Read tridiagonal matrix components obtained by the Lanczos method. .
Definition: Lanczos_EigenValue.c:624
v0
double complex * v0
Definition: global.h:34
BindStruct::Check
struct CheckList Check
Size of the Hilbert space.
Definition: struct.h:411
SumMPI_li
unsigned long int SumMPI_li(unsigned long int idim)
MPI wrapper function to obtain sum of unsigned long integer across processes.
Definition: wrapperMPI.c:239
DefineList::CDataFileHead
char * CDataFileHead
Read from Calcmod in readdef.h. Header of output file such as Green&#39;s function.
Definition: struct.h:42
TimeKeeperWithStep
int TimeKeeperWithStep(struct BindStruct *X, const char *cFileName, const char *cTimeKeeper_Message, const char *cWriteType, const int istep)
Functions for writing a time log.
Definition: log.c:78
eps_Lanczos
double eps_Lanczos
Definition: global.h:155
TimeKeeper
int TimeKeeper(struct BindStruct *X, const char *cFileName, const char *cTimeKeeper_Message, const char *cWriteType)
Functions for writing a time log.
Definition: log.c:42
PhysList::Target_energy
double Target_energy
Is it really used ???
Definition: struct.h:388
DefineList::Lanczos_max
unsigned int Lanczos_max
Maximum number of iterations.
Definition: struct.h:74
stdoutMPI
FILE * stdoutMPI
File pointer to the standard output defined in InitializeMPI()
Definition: global.h:165
DefineList::k_exct
unsigned int k_exct
Read from Calcmod in readdef.h.
Definition: struct.h:47
+ Here is the call graph for this function:
+ Here is the caller graph for this function:

◆ Lanczos_GetTridiagonalMatrixComponents()

int Lanczos_GetTridiagonalMatrixComponents ( struct BindStruct *  X,
double *  _alpha,
double *  _beta,
double complex *  tmp_v1,
unsigned long int *  liLanczos_step 
)

Calculate tridiagonal matrix components by Lanczos method.

Parameters
X[in] Struct to give the information to calculate triangular matrix components.
_alpha[in,out] Triangular matrix components.
_beta[in,out] Triangular matrix components.
tmp_v1[in, out] A temporary vector to calculate triangular matrix components.
liLanczos_step[in] The max iteration step.
Version
1.2
Returns
TRUE
Author
Kazuyoshi Yoshimi (The University of Tokyo)

Definition at line 324 of file Lanczos_EigenValue.c.

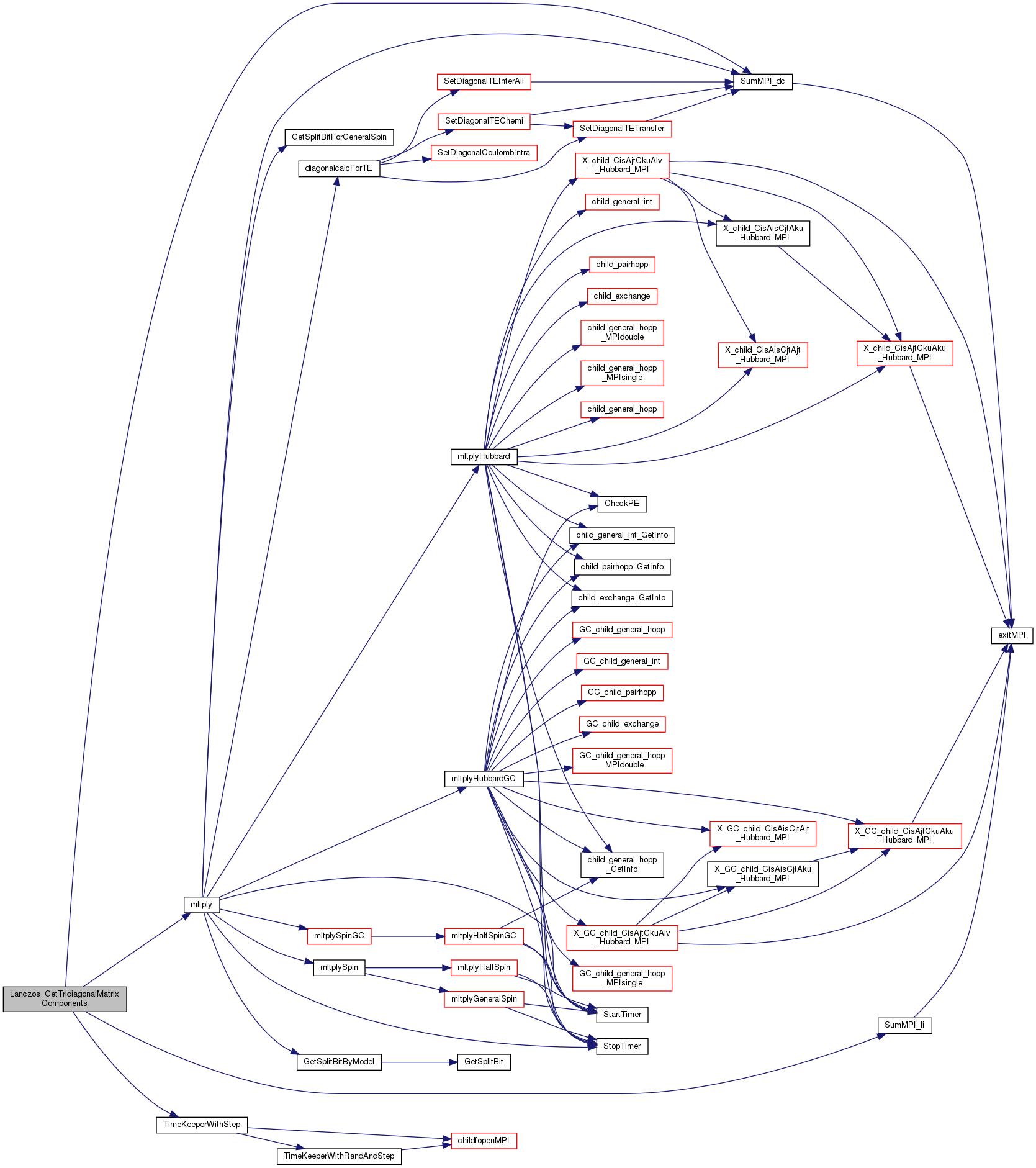
References alpha, beta, c_Lanczos_SpectrumStep, DefineList::CDataFileHead, cFileNameLanczosStep, cFileNameTimeKeep, BindStruct::Check, D_FileNameMax, BindStruct::Def, CheckList::idim_max, DefineList::Lanczos_restart, BindStruct::Large, mltply(), LargeList::prdct, stdoutMPI, SumMPI_dc(), SumMPI_li(), TimeKeeperWithStep(), TRUE, v0, and v1.

Referenced by CalcSpectrumByTPQ().

330  {
331 
332  char sdt[D_FileNameMax];
333  int stp;
334  long int i, i_max;
335  i_max = X->Check.idim_max;
336 
337  unsigned long int i_max_tmp;
338  double beta1, alpha1; //beta,alpha1 should be real
339  double complex temp1, temp2;
340  double complex cbeta1;
341 
342  sprintf(sdt, cFileNameLanczosStep, X->Def.CDataFileHead);
343 
344  /*
345  Set Maximum number of loop to the dimension of the Wavefunction
346  */
347  i_max_tmp = SumMPI_li(i_max);
348  if (i_max_tmp < *liLanczos_step || i_max_tmp < X->Def.LanczosTarget) {
349  *liLanczos_step = i_max_tmp;
350  }
351 
352  if (X->Def.Lanczos_restart == 0) { // initial procedure (not restart)
353 #pragma omp parallel for default(none) private(i) shared(v0, v1, tmp_v1) firstprivate(i_max)
354  for (i = 1; i <= i_max; i++) {
355  v0[i] = 0.0;
356  v1[i] = tmp_v1[i];
357  }
358  stp = 0;
359  mltply(X, v0, tmp_v1);
360  TimeKeeperWithStep(X, cFileNameTimeKeep, c_Lanczos_SpectrumStep, "a", stp);
361  alpha1 = creal(X->Large.prdct);// alpha = v^{\dag}*H*v
362  _alpha[1] = alpha1;
363  cbeta1 = 0.0;
364  fprintf(stdoutMPI, " Step / Step_max alpha beta \n");
365 
366 #pragma omp parallel for reduction(+:cbeta1) default(none) private(i) shared(v0, v1) firstprivate(i_max, alpha1)
367  for (i = 1; i <= i_max; i++) {
368  cbeta1 += conj(v0[i] - alpha1 * v1[i]) * (v0[i] - alpha1 * v1[i]);
369  }
370  cbeta1 = SumMPI_dc(cbeta1);
371  beta1 = creal(cbeta1);
372  beta1 = sqrt(beta1);
373  _beta[1] = beta1;
374  X->Def.Lanczos_restart = 1;
375  } else { // restart case
376  alpha1 = alpha[X->Def.Lanczos_restart];
377  beta1 = beta[X->Def.Lanczos_restart];
378  }
379 
380  for (stp = X->Def.Lanczos_restart + 1; stp <= *liLanczos_step; stp++) {
381 
382  if (fabs(_beta[stp - 1]) < pow(10.0, -14)) {
383  *liLanczos_step = stp - 1;
384  break;
385  }
386 
387 #pragma omp parallel for default(none) private(i, temp1, temp2) shared(v0, v1) firstprivate(i_max, alpha1, beta1)
388  for (i = 1; i <= i_max; i++) {
389  temp1 = v1[i];
390  temp2 = (v0[i] - alpha1 * v1[i]) / beta1;
391  v0[i] = -beta1 * temp1;
392  v1[i] = temp2;
393  }
394 
395  mltply(X, v0, v1);
396  TimeKeeperWithStep(X, cFileNameTimeKeep, c_Lanczos_SpectrumStep, "a", stp);
397  alpha1 = creal(X->Large.prdct);
398  _alpha[stp] = alpha1;
399  cbeta1 = 0.0;
400 
401 #pragma omp parallel for reduction(+:cbeta1) default(none) private(i) shared(v0, v1) firstprivate(i_max, alpha1)
402  for (i = 1; i <= i_max; i++) {
403  cbeta1 += conj(v0[i] - alpha1 * v1[i]) * (v0[i] - alpha1 * v1[i]);
404  }
405  cbeta1 = SumMPI_dc(cbeta1);
406  beta1 = creal(cbeta1);
407  beta1 = sqrt(beta1);
408  _beta[stp] = beta1;
409  if(stp %10 == 0) {
410  fprintf(stdoutMPI, " stp = %d / %lu %.10lf %.10lf \n", stp, *liLanczos_step, alpha1, beta1);
411  }
412  }
413 
414  return TRUE;
415 }
BindStruct::Def
struct DefineList Def
Definision of system (Hamiltonian) etc.
Definition: struct.h:410
mltply
int mltply(struct BindStruct *X, double complex *tmp_v0, double complex *tmp_v1)
Parent function of multiplying the wavefunction by the Hamiltonian. . First, the calculation of diago...
Definition: mltply.c:56
SumMPI_dc
double complex SumMPI_dc(double complex norm)
MPI wrapper function to obtain sum of Double complex across processes.
Definition: wrapperMPI.c:205
CheckList::idim_max
unsigned long int idim_max
The dimension of the Hilbert space of this process.
Definition: struct.h:303
v1
double complex * v1
Definition: global.h:35
LargeList::prdct
double complex prdct
The expectation value of the energy.
Definition: struct.h:314
D_FileNameMax
#define D_FileNameMax
Definition: global.h:23
BindStruct::Large
struct LargeList Large
Variables for Matrix-Vector product.
Definition: struct.h:412
c_Lanczos_SpectrumStep
const char * c_Lanczos_SpectrumStep
Definition: LogMessage.c:76
cFileNameLanczosStep
const char * cFileNameLanczosStep
Definition: global.c:39
TRUE
#define TRUE
Definition: global.h:26
DefineList::Lanczos_restart
int Lanczos_restart
Number of iterations performed in the restart computation.
Definition: struct.h:75
alpha
double * alpha
Definition: global.h:44
cFileNameTimeKeep
const char * cFileNameTimeKeep
Definition: global.c:23
beta
double * beta
Definition: global.h:44
v0
double complex * v0
Definition: global.h:34
BindStruct::Check
struct CheckList Check
Size of the Hilbert space.
Definition: struct.h:411
SumMPI_li
unsigned long int SumMPI_li(unsigned long int idim)
MPI wrapper function to obtain sum of unsigned long integer across processes.
Definition: wrapperMPI.c:239
DefineList::CDataFileHead
char * CDataFileHead
Read from Calcmod in readdef.h. Header of output file such as Green&#39;s function.
Definition: struct.h:42
TimeKeeperWithStep
int TimeKeeperWithStep(struct BindStruct *X, const char *cFileName, const char *cTimeKeeper_Message, const char *cWriteType, const int istep)
Functions for writing a time log.
Definition: log.c:78
stdoutMPI
FILE * stdoutMPI
File pointer to the standard output defined in InitializeMPI()
Definition: global.h:165
+ Here is the call graph for this function:
+ Here is the caller graph for this function:

◆ OutputLanczosVector()

int OutputLanczosVector ( struct BindStruct *  X,
double complex *  tmp_v0,
double complex *  tmp_v1,
unsigned long int  liLanczosStp_vec 
)

Output initial vectors for the restart calculation.

Parameters
X[in] Give the dimension for the vector _v0 and _v1.
tmp_v0[in] The outputted vector for recalculation \( v_0 \).
tmp_v1[in] The outputted vector for recalculation \( v_1 \).
liLanczosStp_vec[in] The step for finishing the iteration.
Return values
-1Fail to output the vector.
0Succeed to output the vector.
Version
2.0
Author
Kazuyoshi Yoshimi (The University of Tokyo)

Definition at line 466 of file Lanczos_EigenValue.c.

References c_OutputSpectrumRecalcvecEnd, c_OutputSpectrumRecalcvecStart, DefineList::CDataFileHead, cFileNameOutputRestartVec, cFileNameTimeKeep, BindStruct::Check, childfopenALL(), D_FileNameMax, BindStruct::Def, CheckList::idim_max, myrank, stdoutMPI, and TimeKeeper().

Referenced by Lanczos_EigenValue().

469  {
470  char sdt[D_FileNameMax];
471  FILE *fp;
472 
473  fprintf(stdoutMPI, " Start: Output vectors for recalculation.\n");
474  TimeKeeper(X, cFileNameTimeKeep, c_OutputSpectrumRecalcvecStart, "a");
475 
476  sprintf(sdt, cFileNameOutputRestartVec, X->Def.CDataFileHead, myrank);
477  if(childfopenALL(sdt, "wb", &fp)!=0){
478  return -1;
479  }
480  fwrite(&liLanczosStp_vec, sizeof(liLanczosStp_vec),1,fp);
481  fwrite(&X->Check.idim_max, sizeof(X->Check.idim_max),1,fp);
482  fwrite(tmp_v0, sizeof(complex double),X->Check.idim_max+1, fp);
483  fwrite(tmp_v1, sizeof(complex double),X->Check.idim_max+1, fp);
484  fclose(fp);
485 
486  fprintf(stdoutMPI, " End: Output vectors for recalculation.\n");
487  TimeKeeper(X, cFileNameTimeKeep, c_OutputSpectrumRecalcvecEnd, "a");
488  return 0;
489 }
childfopenALL
int childfopenALL(const char *_cPathChild, const char *_cmode, FILE **_fp)
All processes open file in output/ directory.
Definition: FileIO.c:50
BindStruct::Def
struct DefineList Def
Definision of system (Hamiltonian) etc.
Definition: struct.h:410
CheckList::idim_max
unsigned long int idim_max
The dimension of the Hilbert space of this process.
Definition: struct.h:303
D_FileNameMax
#define D_FileNameMax
Definition: global.h:23
cFileNameOutputRestartVec
const char * cFileNameOutputRestartVec
Definition: global.c:81
c_OutputSpectrumRecalcvecEnd
const char * c_OutputSpectrumRecalcvecEnd
Definition: LogMessage.c:71
cFileNameTimeKeep
const char * cFileNameTimeKeep
Definition: global.c:23
myrank
int myrank
Process ID, defined in InitializeMPI()
Definition: global.h:163
c_OutputSpectrumRecalcvecStart
const char * c_OutputSpectrumRecalcvecStart
Definition: LogMessage.c:70
BindStruct::Check
struct CheckList Check
Size of the Hilbert space.
Definition: struct.h:411
DefineList::CDataFileHead
char * CDataFileHead
Read from Calcmod in readdef.h. Header of output file such as Green&#39;s function.
Definition: struct.h:42
TimeKeeper
int TimeKeeper(struct BindStruct *X, const char *cFileName, const char *cTimeKeeper_Message, const char *cWriteType)
Functions for writing a time log.
Definition: log.c:42
stdoutMPI
FILE * stdoutMPI
File pointer to the standard output defined in InitializeMPI()
Definition: global.h:165
+ Here is the call graph for this function:
+ Here is the caller graph for this function:

◆ OutputTMComponents()

int OutputTMComponents ( struct BindStruct *  X,
double *  _alpha,
double *  _beta,
double  _dnorm,
int  liLanczosStp 
)

Output tridiagonal matrix components obtained by the Lanczos method.

Parameters
X[in] Give the input file name.
_alpha[in] The array of tridiagonal matrix components.
_beta[in] The array of tridiagonal matrix components.
_dnorm[in] The norm.
liLanczosStp[in] The iteration step.
Return values
FALSEFail to open the file for the output.
TRUESucceed to open the file for the output.
Version
1.2
Author
Kazuyoshi Yoshimi (The University of Tokyo)

Definition at line 697 of file Lanczos_EigenValue.c.

References DefineList::CDataFileHead, cFileNameTridiagonalMatrixComponents, childfopenMPI(), D_FileNameMax, BindStruct::Def, FALSE, and TRUE.

Referenced by CalcSpectrumByTPQ(), and Lanczos_EigenValue().

704 {
705  char sdt[D_FileNameMax];
706  unsigned long int i;
707  FILE *fp;
708 
709  sprintf(sdt, cFileNameTridiagonalMatrixComponents, X->Def.CDataFileHead);
710  if(childfopenMPI(sdt,"w", &fp)!=0){
711  return FALSE;
712  }
713  fprintf(fp, "%d \n",liLanczosStp);
714  fprintf(fp, "%.10lf \n",_dnorm);
715  for( i = 1 ; i <= liLanczosStp; i++){
716  fprintf(fp,"%.10lf %.10lf \n", _alpha[i], _beta[i]);
717  }
718  fclose(fp);
719  return TRUE;
720 }
BindStruct::Def
struct DefineList Def
Definision of system (Hamiltonian) etc.
Definition: struct.h:410
D_FileNameMax
#define D_FileNameMax
Definition: global.h:23
childfopenMPI
int childfopenMPI(const char *_cPathChild, const char *_cmode, FILE **_fp)
Only the root process open file in output/ directory.
Definition: FileIO.c:27
TRUE
#define TRUE
Definition: global.h:26
cFileNameTridiagonalMatrixComponents
const char * cFileNameTridiagonalMatrixComponents
Definition: global.c:52
FALSE
#define FALSE
Definition: global.h:25
DefineList::CDataFileHead
char * CDataFileHead
Read from Calcmod in readdef.h. Header of output file such as Green&#39;s function.
Definition: struct.h:42
+ Here is the call graph for this function:
+ Here is the caller graph for this function:

◆ ReadInitialVector()

int ReadInitialVector ( struct BindStruct *  X,
double complex *  _v0,
double complex *  _v1,
unsigned long int *  liLanczosStp_vec 
)

Read initial vectors for the restart calculation.

Parameters
X[in] Give the dimension for the vector _v0 and _v1.
_v0[out] The inputted vector for recalculation \( v_0 \).
_v1[out] The inputted vector for recalculation \( v_1 \).
liLanczosStp_vec[in] The max iteration step.
Return values
-1Fail to read the initial vector.
0Succeed to read the initial vector.
Version
1.2
Author
Kazuyoshi Yoshimi (The University of Tokyo)

Definition at line 428 of file Lanczos_EigenValue.c.

References c_InputSpectrumRecalcvecEnd, c_InputSpectrumRecalcvecStart, DefineList::CDataFileHead, cFileNameOutputRestartVec, cFileNameTimeKeep, BindStruct::Check, childfopenALL(), D_FileNameMax, BindStruct::Def, CheckList::idim_max, myrank, stdoutMPI, and TimeKeeper().

Referenced by Lanczos_EigenValue().

429 {
430  size_t byte_size;
431  char sdt[D_FileNameMax];
432  FILE *fp;
433  unsigned long int i_max;
434 
435  fprintf(stdoutMPI, " Start: Input vectors for recalculation.\n");
436  TimeKeeper(X, cFileNameTimeKeep, c_InputSpectrumRecalcvecStart, "a");
437  sprintf(sdt, cFileNameOutputRestartVec, X->Def.CDataFileHead, myrank);
438  if (childfopenALL(sdt, "rb", &fp) != 0) {
439  return -1;
440  }
441  byte_size = fread(liLanczosStp_vec, sizeof(*liLanczosStp_vec),1,fp);
442  byte_size = fread(&i_max, sizeof(long int), 1, fp);
443  if(i_max != X->Check.idim_max){
444  fprintf(stderr, "Error: A size of Inputvector is incorrect.\n");
445  return -1;
446  }
447  byte_size = fread(_v0, sizeof(complex double), X->Check.idim_max + 1, fp);
448  byte_size = fread(_v1, sizeof(complex double), X->Check.idim_max + 1, fp);
449  fclose(fp);
450  fprintf(stdoutMPI, " End: Input vectors for recalculation.\n");
451  TimeKeeper(X, cFileNameTimeKeep, c_InputSpectrumRecalcvecEnd, "a");
452  if (byte_size == 0) printf("byte_size: %d \n", (int)byte_size);
453  return 0;
454 }
childfopenALL
int childfopenALL(const char *_cPathChild, const char *_cmode, FILE **_fp)
All processes open file in output/ directory.
Definition: FileIO.c:50
BindStruct::Def
struct DefineList Def
Definision of system (Hamiltonian) etc.
Definition: struct.h:410
CheckList::idim_max
unsigned long int idim_max
The dimension of the Hilbert space of this process.
Definition: struct.h:303
D_FileNameMax
#define D_FileNameMax
Definition: global.h:23
cFileNameOutputRestartVec
const char * cFileNameOutputRestartVec
Definition: global.c:81
c_InputSpectrumRecalcvecStart
const char * c_InputSpectrumRecalcvecStart
Definition: LogMessage.c:72
cFileNameTimeKeep
const char * cFileNameTimeKeep
Definition: global.c:23
c_InputSpectrumRecalcvecEnd
const char * c_InputSpectrumRecalcvecEnd
Definition: LogMessage.c:73
myrank
int myrank
Process ID, defined in InitializeMPI()
Definition: global.h:163
BindStruct::Check
struct CheckList Check
Size of the Hilbert space.
Definition: struct.h:411
DefineList::CDataFileHead
char * CDataFileHead
Read from Calcmod in readdef.h. Header of output file such as Green&#39;s function.
Definition: struct.h:42
TimeKeeper
int TimeKeeper(struct BindStruct *X, const char *cFileName, const char *cTimeKeeper_Message, const char *cWriteType)
Functions for writing a time log.
Definition: log.c:42
stdoutMPI
FILE * stdoutMPI
File pointer to the standard output defined in InitializeMPI()
Definition: global.h:165
+ Here is the call graph for this function:
+ Here is the caller graph for this function:

◆ ReadTMComponents()

int ReadTMComponents ( struct BindStruct *  X,
double *  _dnorm,
unsigned long int *  _i_max,
int  iFlg 
)

Read tridiagonal matrix components obtained by the Lanczos method.
.

Note
The arrays of tridiaonal components alpha and beta are global arrays.
Parameters
X[in] Give the iteration number for the recalculation and the input file name.
_dnorm[out] Get the norm.
_i_max[in] The iteration step for the input data.
iFlg[in] Flag for the recalculation.
Return values
FALSEFail to read the file.
TRUESucceed to read the file.
Version
1.2
Author
Kazuyoshi Yoshimi (The University of Tokyo)

Definition at line 624 of file Lanczos_EigenValue.c.

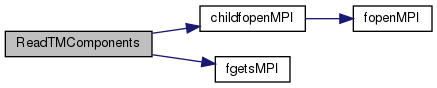
References alpha, beta, DefineList::CDataFileHead, cFileNameTridiagonalMatrixComponents, childfopenMPI(), D_FileNameMax, BindStruct::Def, FALSE, fgetsMPI(), DefineList::Lanczos_max, DefineList::LanczosTarget, DefineList::nvec, TRUE, and vec.

Referenced by CalcSpectrumByTPQ(), and Lanczos_EigenValue().

629  {
630  char sdt[D_FileNameMax];
631  char ctmp[256];
632 
633  unsigned long int idx, i, ivec;
634  unsigned long int i_max;
635  double dnorm;
636  FILE *fp;
637  idx=1;
638  sprintf(sdt, cFileNameTridiagonalMatrixComponents, X->Def.CDataFileHead);
639  if(childfopenMPI(sdt,"r", &fp)!=0){
640  return FALSE;
641  }
642 
643  fgetsMPI(ctmp, sizeof(ctmp)/sizeof(char), fp);
644  sscanf(ctmp,"%ld \n", &i_max);
645  if (X->Def.LanczosTarget > X->Def.nvec) {
646  ivec = X->Def.LanczosTarget + 1;
647  }
648  else {
649  ivec =X->Def.nvec + 1;
650  }
651 
652  if(iFlg==0) {
653  alpha = (double *) realloc(alpha, sizeof(double) * (i_max + X->Def.Lanczos_max + 1));
654  beta = (double *) realloc(beta, sizeof(double) * (i_max + X->Def.Lanczos_max + 1));
655  vec[0] = (complex double *) realloc(vec[0], ivec*(i_max + X->Def.Lanczos_max + 1) * sizeof(complex double));
656  for (i = 0; i < ivec; i++) {
657  vec[i] = vec[0] + i*(i_max + X->Def.Lanczos_max + 1);
658  }
659  }
660  else if(iFlg==1){
661  alpha=(double*)realloc(alpha, sizeof(double)*(i_max + 1));
662  beta=(double*)realloc(beta, sizeof(double)*(i_max + 1));
663  vec[0] = (complex double *) realloc(vec[0], ivec*(i_max + 1) * sizeof(complex double));
664  for (i = 0; i < ivec; i++) {
665  vec[i] = vec[0] + i*(i_max +1);
666  //vec[i] = (complex double *) realloc(vec[i], (i_max + X->Def.Lanczos_max + 1) * sizeof(complex double));
667  }
668  }
669  else{
670  fclose(fp);
671  return FALSE;
672  }
673  fgetsMPI(ctmp, sizeof(ctmp)/sizeof(char), fp);
674  sscanf(ctmp,"%lf \n", &dnorm);
675  while(fgetsMPI(ctmp, sizeof(ctmp)/sizeof(char), fp) != NULL){
676  sscanf(ctmp,"%lf %lf \n", &alpha[idx], &beta[idx]);
677  idx++;
678  }
679  fclose(fp);
680  *_dnorm=dnorm;
681  *_i_max=i_max;
682  return TRUE;
683 }
BindStruct::Def
struct DefineList Def
Definision of system (Hamiltonian) etc.
Definition: struct.h:410
D_FileNameMax
#define D_FileNameMax
Definition: global.h:23
vec
double complex ** vec
Definition: global.h:45
childfopenMPI
int childfopenMPI(const char *_cPathChild, const char *_cmode, FILE **_fp)
Only the root process open file in output/ directory.
Definition: FileIO.c:27
DefineList::nvec
unsigned int nvec
Read from Calcmod in readdef.h.
Definition: struct.h:46
TRUE
#define TRUE
Definition: global.h:26
cFileNameTridiagonalMatrixComponents
const char * cFileNameTridiagonalMatrixComponents
Definition: global.c:52
alpha
double * alpha
Definition: global.h:44
FALSE
#define FALSE
Definition: global.h:25
beta
double * beta
Definition: global.h:44
DefineList::LanczosTarget
int LanczosTarget
Which eigenstate is used to check convergence. Read from Calcmod in readdef.h.
Definition: struct.h:50
fgetsMPI
char * fgetsMPI(char *InputString, int maxcount, FILE *fp)
MPI file I/O (get a line, fgets) wrapper. Only the root node (myrank = 0) reads and broadcast string...
Definition: wrapperMPI.c:122
DefineList::CDataFileHead
char * CDataFileHead
Read from Calcmod in readdef.h. Header of output file such as Green&#39;s function.
Definition: struct.h:42
DefineList::Lanczos_max
unsigned int Lanczos_max
Maximum number of iterations.
Definition: struct.h:74
+ Here is the call graph for this function:
+ Here is the caller graph for this function:

◆ SetInitialVector()

void SetInitialVector ( struct BindStruct *  X,
double complex *  tmp_v0,
double complex *  tmp_v1 
)

Set initial vector to start the calculation for Lanczos method.
.

Parameters
X[in, out] Get the information of reading initisl vectors.
Input: idim_max, iFlgMPI, k_exct, iInitialVecType.
Output: Large.iv.
tmp_v0[out] The initial vector whose components are zero.
tmp_v1[out] The initial vector whose components are randomly given when initial_mode=1, otherwise, iv-th component is only given.

Definition at line 499 of file Lanczos_EigenValue.c.

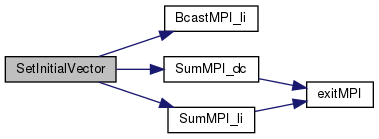
References BcastMPI_li(), BindStruct::Check, BindStruct::Def, CheckList::idim_max, DefineList::iFlgMPI, DefineList::iInitialVecType, DefineList::initial_iv, initial_mode, LargeList::iv, DefineList::k_exct, BindStruct::Large, myrank, nproc, nthreads, stdoutMPI, SumMPI_dc(), and SumMPI_li().

Referenced by Lanczos_EigenValue().

499  {
500  int iproc;
501  long int i, iv, i_max;
502  unsigned long int i_max_tmp, sum_i_max;
503  int mythread;
504 
505 // for GC
506  double dnorm;
507  double complex cdnorm;
508  long unsigned int u_long_i;
509  dsfmt_t dsfmt;
510 
511  i_max = X->Check.idim_max;
512  if (initial_mode == 0) {
513  if(X->Def.iFlgMPI==0) {
514  sum_i_max = SumMPI_li(X->Check.idim_max);
515  }
516  else{
517  sum_i_max =X->Check.idim_max;
518  }
519  X->Large.iv = (sum_i_max / 2 + X->Def.initial_iv) % sum_i_max + 1;
520  iv = X->Large.iv;
521  fprintf(stdoutMPI, " initial_mode=%d normal: iv = %ld i_max=%ld k_exct =%d \n\n", initial_mode, iv, i_max,
522  X->Def.k_exct);
523 #pragma omp parallel for default(none) private(i) shared(tmp_v0, tmp_v1) firstprivate(i_max)
524  for (i = 1; i <= i_max; i++) {
525  tmp_v0[i] = 0.0;
526  tmp_v1[i] = 0.0;
527  }
528 
529  sum_i_max = 0;
530  if(X->Def.iFlgMPI==0) {
531  for (iproc = 0; iproc < nproc; iproc++) {
532  i_max_tmp = BcastMPI_li(iproc, i_max);
533  if (sum_i_max <= iv && iv < sum_i_max + i_max_tmp) {
534  if (myrank == iproc) {
535  tmp_v1[iv - sum_i_max + 1] = 1.0;
536  if (X->Def.iInitialVecType == 0) {
537  tmp_v1[iv - sum_i_max + 1] += 1.0 * I;
538  tmp_v1[iv - sum_i_max + 1] /= sqrt(2.0);
539  }
540  }/*if (myrank == iproc)*/
541  }/*if (sum_i_max <= iv && iv < sum_i_max + i_max_tmp)*/
542 
543  sum_i_max += i_max_tmp;
544 
545  }/*for (iproc = 0; iproc < nproc; iproc++)*/
546  }
547  else {
548  tmp_v1[iv + 1] = 1.0;
549  if (X->Def.iInitialVecType == 0) {
550  tmp_v1[iv + 1] += 1.0 * I;
551  tmp_v1[iv + 1] /= sqrt(2.0);
552  }
553  }
554  }/*if(initial_mode == 0)*/
555  else if (initial_mode == 1) {
556  iv = X->Def.initial_iv;
557  fprintf(stdoutMPI, " initial_mode=%d (random): iv = %ld i_max=%ld k_exct =%d \n\n", initial_mode, iv, i_max,
558  X->Def.k_exct);
559 #pragma omp parallel default(none) private(i, u_long_i, mythread, dsfmt) \
560  shared(tmp_v0, tmp_v1, iv, X, nthreads, myrank) firstprivate(i_max)
561  {
562 
563 #pragma omp for
564  for (i = 1; i <= i_max; i++) {
565  tmp_v0[i] = 0.0;
566  }
567  /*
568  Initialise MT
569  */
570 #ifdef _OPENMP
571  mythread = omp_get_thread_num();
572 #else
573  mythread = 0;
574 #endif
575  if(X->Def.iFlgMPI==0) {
576  u_long_i = 123432 + labs(iv) + mythread + nthreads * myrank;
577  }
578  else{
579  u_long_i = 123432 + labs(iv)+ mythread ;
580  }
581  dsfmt_init_gen_rand(&dsfmt, u_long_i);
582 
583  if (X->Def.iInitialVecType == 0) {
584 #pragma omp for
585  for (i = 1; i <= i_max; i++)
586  tmp_v1[i] = 2.0 * (dsfmt_genrand_close_open(&dsfmt) - 0.5) +
587  2.0 * (dsfmt_genrand_close_open(&dsfmt) - 0.5) * I;
588  } else {
589 #pragma omp for
590  for (i = 1; i <= i_max; i++)
591  tmp_v1[i] = 2.0 * (dsfmt_genrand_close_open(&dsfmt) - 0.5);
592  }
593 
594  }/*#pragma omp parallel*/
595 
596  cdnorm = 0.0;
597 #pragma omp parallel for default(none) private(i) shared(tmp_v1, i_max) reduction(+: cdnorm)
598  for (i = 1; i <= i_max; i++) {
599  cdnorm += conj(tmp_v1[i]) * tmp_v1[i];
600  }
601  if(X->Def.iFlgMPI==0) {
602  cdnorm = SumMPI_dc(cdnorm);
603  }
604  dnorm = creal(cdnorm);
605  dnorm = sqrt(dnorm);
606 #pragma omp parallel for default(none) private(i) shared(tmp_v1) firstprivate(i_max, dnorm)
607  for (i = 1; i <= i_max; i++) {
608  tmp_v1[i] = tmp_v1[i] / dnorm;
609  }
610  }/*else if(initial_mode==1)*/
611 }
BindStruct::Def
struct DefineList Def
Definision of system (Hamiltonian) etc.
Definition: struct.h:410
SumMPI_dc
double complex SumMPI_dc(double complex norm)
MPI wrapper function to obtain sum of Double complex across processes.
Definition: wrapperMPI.c:205
CheckList::idim_max
unsigned long int idim_max
The dimension of the Hilbert space of this process.
Definition: struct.h:303
initial_mode
int initial_mode
Definition: global.h:60
BcastMPI_li
unsigned long int BcastMPI_li(int root, unsigned long int idim)
MPI wrapper function to broadcast unsigned long integer across processes.
Definition: wrapperMPI.c:273
BindStruct::Large
struct LargeList Large
Variables for Matrix-Vector product.
Definition: struct.h:412
nthreads
int nthreads
Number of Threads, defined in InitializeMPI()
Definition: global.h:164
LargeList::iv
long int iv
Used for initializing vector.
Definition: struct.h:316
nproc
int nproc
Number of processors, defined in InitializeMPI()
Definition: global.h:162
DefineList::iFlgMPI
int iFlgMPI
MPI mode.
Definition: struct.h:225
DefineList::initial_iv
long int initial_iv
Seed of random number for initial guesss of wavefunctions.
Definition: struct.h:76
myrank
int myrank
Process ID, defined in InitializeMPI()
Definition: global.h:163
DefineList::iInitialVecType
int iInitialVecType
Switch for type of inital vectors. 0:complex type, 1: real type. default value is set as 0 in readdef...
Definition: struct.h:195
BindStruct::Check
struct CheckList Check
Size of the Hilbert space.
Definition: struct.h:411
SumMPI_li
unsigned long int SumMPI_li(unsigned long int idim)
MPI wrapper function to obtain sum of unsigned long integer across processes.
Definition: wrapperMPI.c:239
stdoutMPI
FILE * stdoutMPI
File pointer to the standard output defined in InitializeMPI()
Definition: global.h:165
DefineList::k_exct
unsigned int k_exct
Read from Calcmod in readdef.h.
Definition: struct.h:47
+ Here is the call graph for this function:
+ Here is the caller graph for this function: