レプリカ交換モンテカルロ法による探索¶
ここでは、レプリカ交換モンテカルロ法によって、回折データから原子座標を解析する方法について説明します。
具体的な計算手順は minsearch の時と同様です。
サンプルファイルの場所¶
サンプルファイルは sample/sim-threpd-rheed/single_beam/exchange にあります。
フォルダには以下のファイルが格納されています。
bulk.txtbulk.exeの入力ファイルexperiment.txt,template.txtメインプログラムでの計算を進めるための参照ファイル
ref.txt計算が正しく実行されたか確認するためのファイル(本チュートリアルを行うことで得られる
best_result.txtの回答)。input.tomlメインプログラムの入力ファイル
prepare.sh,do.sh本チュートリアルを一括計算するために準備されたスクリプト
以下、これらのファイルについて説明したあと、実際の計算結果を紹介します。
参照ファイルの説明¶
template.txt , experiment.txt については、
前のチュートリアル(Nealder-Mead法による最適化)と同じものを使用します。
入力ファイルの説明¶
ここでは、メインプログラム用の入力ファイル input.toml について説明します。
input.toml の詳細については入力ファイルに記載されています。
以下は、サンプルファイルにある input.toml の中身になります。
[base]
dimension = 2
[algorithm]
name = "exchange"
label_list = ["z1", "z2"]
seed = 12345
[algorithm.param]
min_list = [3.0, 3.0]
max_list = [6.0, 6.0]
[algorithm.exchange]
numsteps = 1000
numsteps_exchange = 20
Tmin = 0.005
Tmax = 0.05
Tlogspace = true
[solver]
name = "sim-trhepd-rheed"
[solver.config]
calculated_first_line = 5
calculated_last_line = 74
row_number = 2
[solver.param]
string_list = ["value_01", "value_02" ]
degree_max = 7.0
[solver.reference]
path = "experiment.txt"
first = 1
last = 70
ここではこの入力ファイルを簡単に説明します。 詳細は入力ファイルのレファレンスを参照してください。
[base] セクションはメインプログラム全体のパラメータです。
dimension は最適化したい変数の個数で、今の場合は2つの変数の最適化を行うので、2 を指定します。
[algorithm] セクションは用いる探索アルゴリズムを設定します。
交換モンテカルロ法を用いる場合には、 name に "exchange" を指定します。
label_list は、value_0x (x=1,2) を出力する際につけるラベル名のリストです。
seed は擬似乱数生成器に与える種です。
[algorithm.param] サブセクションは、最適化したいパラメータの範囲などを指定します。
min_list は最小値、 max_list は最大値を示します。
[algorithm.exchange] サブセクションは、交換モンテカルロ法のハイパーパラメータを指定します。
numstepはモンテカルロ更新の回数です。numsteps_exchangeで指定した回数のモンテカルロ更新の後に、温度交換を試みます。Tmin,Tmaxはそれぞれ温度の下限・上限です。Tlogspaceがtrueの場合、温度を対数空間で等分割します
[solver] セクションではメインプログラムの内部で使用するソルバーを指定します。
minsearch のチュートリアルを参照してください。
計算実行¶
最初にサンプルファイルが置いてあるフォルダへ移動します(以下、本ソフトウェアをダウンロードしたディレクトリ直下にいることを仮定します).
cd sample/sim-trhepd-rheed/single_beam/exchange
順問題の時と同様に、 bulk.exe と surf.exe をコピーします。
cp ../../../../../sim-trhepd-rheed/src/TRHEPD/bulk.exe .
cp ../../../../../sim-trhepd-rheed/src/TRHEPD/surf.exe .
最初に bulk.exe を実行し、bulkP.b を作成します。
./bulk.exe
そのあとに、メインプログラムを実行します(計算時間は通常のPCで数秒程度で終わります)。
mpiexec -np 4 python3 ../../../../src/py2dmat_main.py input.toml | tee log.txt
ここではプロセス数4のMPI並列を用いた計算を行っています。
(Open MPI を用いる場合で、使えるコア数よりも要求プロセス数の方が多い時には、
mpiexec コマンドに --oversubscribed オプションを追加してください。)
実行すると、各ランクのフォルダが作成され、
各モンテカルロステップで評価したパラメータおよび目的関数の値を記した trial.txt ファイルと、
実際に採択されたパラメータを記した result.txt ファイルが作成されます。
ともに書式は同じで、最初の2列がステップ数とプロセス内のwalker 番号、次が温度、3列目が目的関数の値、4列目以降がパラメータです。
# step walker T fx x1 x2
0 0 0.004999999999999999 0.07830821484593968 3.682008067401509 3.9502750191292586
1 0 0.004999999999999999 0.07830821484593968 3.682008067401509 3.9502750191292586
2 0 0.004999999999999999 0.07830821484593968 3.682008067401509 3.9502750191292586
3 0 0.004999999999999999 0.06273922648753057 4.330900869594549 4.311333132184154
また、 sim-trhepd-rheed ソルバーの場合は、 各作業フォルダの下にサブフォルダ Log%%%%% ( %%%%% がグリッドのid)が作成され、ロッキングカーブの情報などが記録されます
(各プロセスにおけるモンテカルロステップ数がidとして割り振られます)。
最後に、 best_result.txt に、目的関数 (R-factor) が最小となったパラメータとそれを得たランク、モンテカルロステップの情報が書き込まれます。
nprocs = 4
rank = 2
step = 65
fx = 0.008233957976993406
x[0] = 4.221129370933539
x[1] = 5.139591716517661
なお、一括計算するスクリプトとして do.sh を用意しています。
do.sh では best_result.txt と ref.txt の差分も比較しています。
以下、説明は割愛しますが、その中身を掲載します。
sh prepare.sh
./bulk.exe
time mpiexec --oversubscribe -np 4 python3 ../../../../src/py2dmat_main.py input.toml
echo diff best_result.txt ref.txt
res=0
diff best_result.txt ref.txt || res=$?
if [ $res -eq 0 ]; then
echo TEST PASS
true
else
echo TEST FAILED: best_result.txt and ref.txt differ
false
fi
後処理¶
各ランクフォルダにある result.txt には、各レプリカでサンプリングされたデータが記録されていますが、
Py2DMat の実装では同一レプリカが様々な温度のサンプルを保持しています。
2DMat は、全レプリカの結果から温度ごとのサンプルに整列し直す script/separateT.py スクリプトを提供しています。
python3 ../../../../script/separateT.py
result_T%.txt に各温度点ごとにまとめなおされたデータが書き込まれます(% は温度点のindex)。
1列目がステップ、2列めがランク、3列目が目的関数の値、4列目以降がパラメータです。
# T = 0.004999999999999999
# step rank fx x1 x2
0 0 0.07830821484593968 3.682008067401509 3.9502750191292586
1 0 0.07830821484593968 3.682008067401509 3.9502750191292586
2 0 0.07830821484593968 3.682008067401509 3.9502750191292586
計算結果の可視化¶
result_T%.txt を図示することで、 R-factor の小さいパラメータがどこにあるかを推定することができます。
今回の場合は、以下のコマンドをうつことで2次元パラメータ空間の図 result.png が作成されます。
python3 plot_result_2d.py
作成された図を見ると、(5.25, 4.25) と (4.25, 5.25) 付近にサンプルが集中していることと、
R-factor の値が小さいことがわかります。
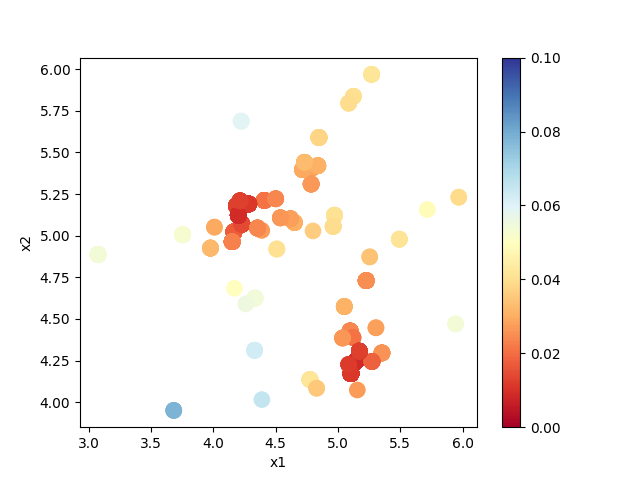
サンプルされたパラメータと R-factor 。横軸は value_01 , 縦軸は value_02 を表す。¶
また、 RockingCurve.txt が各サブフォルダに格納されています。
LogXXX_YYY の XXX はモンテカルロのステップ数、 YYY は各MPIプロセス内のレプリカの番号です。
これを用いることで、前チュートリアルの手順に従い、実験値との比較も行うことが可能です。