制約式を適用したレプリカ交換モンテカルロ法による探索¶
ここでは、 [runner.limitation] セクションに設定できる制約式機能のチュートリアルを示します。
例として、レプリカ交換モンテカルロ法を、Himmelblauを対象に探索する計算に制約式を適用します。
サンプルファイルの場所¶
サンプルファイルは sample/analytical/limitation にあります。
フォルダには以下のファイルが格納されています。
ref.txt計算が正しく実行されたか確認するためのファイル(本チュートリアルを行うことで得られる
best_result.txtの回答)。input.tomlメインプログラムの入力ファイル。
do.sh本チュートリアルを一括計算するために準備されたスクリプト
以下、これらのファイルについて説明したあと、実際の計算結果を紹介します。
入力ファイルの説明¶
メインプログラム用の入力ファイル input.toml について説明します。
input.toml の詳細については入力ファイルに記載されています。
以下は、サンプルファイルにある input.toml の中身になります。
[base]
dimension = 2
output_dir = "output"
[algorithm]
name = "exchange"
seed = 12345
[algorithm.param]
max_list = [6.0, 6.0]
min_list = [-6.0, -6.0]
unit_list = [0.3, 0.3]
[algorithm.exchange]
Tmin = 1.0
Tmax = 100000.0
numsteps = 10000
numsteps_exchange = 100
[solver]
name = "analytical"
function_name = "himmelblau"
[runner]
[runner.limitation]
co_a = [[1, -1],[1, 1]]
co_b = [[0], [-1]]
ここではこの入力ファイルを簡単に説明します。 詳細は入力ファイルのレファレンスを参照してください。
[base] セクションはメインプログラム全体のパラメータです。
dimension は最適化したい変数の個数で、今の場合は2つの変数の最適化を行うので、2 を指定します。
[algorithm] セクションは用いる探索アルゴリズムを設定します。
交換モンテカルロ法を用いる場合には、 name に "exchange" を指定します。
seed は擬似乱数生成器に与える種です。
[algorithm.param] サブセクションは、最適化したいパラメータの範囲などを指定します。
min_list は最小値、 max_list は最大値を示します。
[algorithm.exchange] サブセクションは、交換モンテカルロ法のハイパーパラメータを指定します。
numstepはモンテカルロ更新の回数です。numsteps_exchangeで指定した回数のモンテカルロ更新の後に、温度交換を試みます。Tmin,Tmaxはそれぞれ温度の下限・上限です。Tlogspaceがtrueの場合、温度を対数空間で等分割します。このオプションはデフォルト値がtrueであるため、今回のinput.tomlに指定は無いですが、trueになっています。
[solver] セクションではメインプログラムの内部で使用するソルバーを指定します。
今回は analytical ソルバーを指定しています。 analytical ソルバーは function_name パラメータを用いて関数を設定します。
今回はHimmelblau 関数を指定しています。
analytical ソルバーに関してはチュートリアル「順問題ソルバーの追加」を参照してください。
[runner] セクションは [runner.limitation] サブセクションを持ち、この中に制約式を設定します。
現在、制約式は \(N\) 次元のパラメータ \(x\) 、 \(M\) 行 \(N\) 列の行列 \(A\) 、
\(M\) 次元の縦ベクトル \(b\) から定義される \(Ax+b>0\) の制約式が利用可能です。
パラメータとしては、以下の項目が設定可能です。
co_aは行列 \(A\) を設定します。co_bは縦ベクトル \(b\) を設定します。
パラメータの詳しい設定方法はマニュアル内「入力ファイル」項の「 [limitation] セクション」を参照してください。
今回は
の制約式を課して実行しています。
計算実行¶
最初にサンプルファイルが置いてあるフォルダへ移動します(以下、本ソフトウェアをダウンロードしたディレクトリ直下にいることを仮定します).
cd sample/analytical/limitation
そのあとに、メインプログラムを実行します(計算時間は通常のPCで20秒程度で終わります)。
mpiexec -np 10 python3 ../../../src/py2dmat_main.py input.toml | tee log.txt
ここではプロセス数10のMPI並列を用いた計算を行っています。
(Open MPI を用いる場合で、使えるコア数よりも要求プロセス数の方が多い時には、
mpiexec コマンドに --oversubscribed オプションを追加してください。)
実行すると、 output フォルダが生成され、その中に各ランクのフォルダが作成されます。
更にその中には、各モンテカルロステップで評価したパラメータおよび目的関数の値を記した trial.txt ファイルと、
実際に採択されたパラメータを記した result.txt ファイルが作成されます。
ともに書式は同じで、最初の2列がステップ数とプロセス内のwalker 番号、次が温度、3列目が目的関数の値、4列目以降がパラメータです。
以下は、 output/0/result.txt ファイルの冒頭部分です。
# step walker T fx x1 x2
0 0 1.0 187.94429125133564 5.155393113805774 -2.203493345018569
1 0 1.0 148.23606736778044 4.9995614992887525 -2.370212436322816
2 0 1.0 148.23606736778044 4.9995614992887525 -2.370212436322816
3 0 1.0 148.23606736778044 4.9995614992887525 -2.370212436322816
最後に、 output/best_result.txt に、目的関数が最小となったパラメータとそれを得たランク、モンテカルロステップの情報が書き込まれます。
nprocs = 10
rank = 2
step = 4523
walker = 0
fx = 0.00010188398524402734
x1 = 3.584944906595298
x2 = -1.8506985826548874
なお、一括計算するスクリプトとして do.sh を用意しています。
do.sh では best_result.txt と ref.txt の差分も比較しています。
以下、説明は割愛しますが、その中身を掲載します。
#!/bin/bash
mpiexec -np 10 --oversubscribe python3 ../../../src/py2dmat_main.py input.toml
echo diff output/best_result.txt ref.txt
res=0
diff output/best_result.txt ref.txt || res=$?
if [ $res -eq 0 ]; then
echo TEST PASS
true
else
echo TEST FAILED: best_result.txt and ref.txt differ
false
fi
計算結果の可視化¶
result.txt を図示して、制約式を満たした座標のみを探索しているかを確認します。
今回の場合は、以下のコマンドを打つことで2次元パラメータ空間の図が <実行日>_histogram フォルダ内に作成されます。
生成されるヒストグラムは、burn-in期間として最初の1000ステップ分の探索を捨てたデータを使用しています。
python3 hist2d_limitation_sample.py -p 10 -i input.toml -b 0.1
作成された図には2本の直線 \(x_{1} − x_{2} = 0, x_{1} + x_{2} − 1 = 0\) と 探索結果(事後確率分布のヒストグラム)を図示しています。 図を見ると \(x_{1} − x_{2} > 0, x_{1} + x_{2} − 1 > 0\) の範囲のみ探索をしていることが確認できます。 以下に図の一部を掲載します。
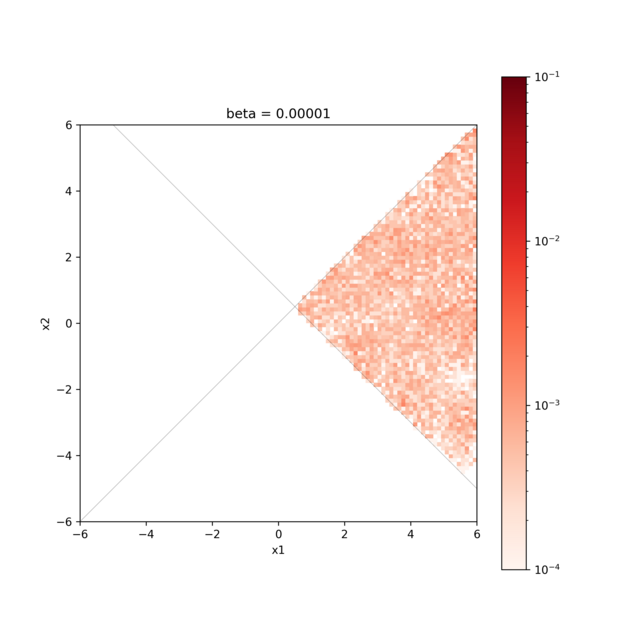
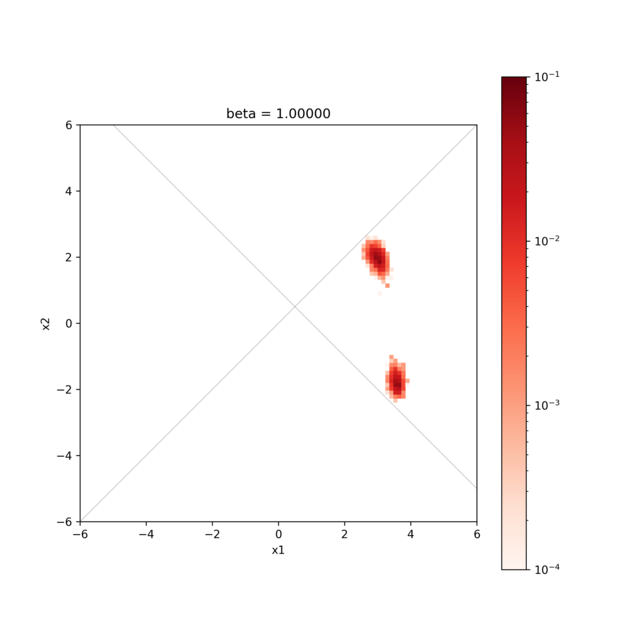
サンプルされたパラメータと確率分布。横軸は value_01 (x1) , 縦軸は value_02 (x2) を表す。¶