Exact diagonalization solver: pomerol

pomerol is an exact diagonalization (ED) library implemented in c++. DCore provides an interface to pomerol library to compute an approximate solution of DMFT with discritized hybridization function.

Features

  • Arbitrary temperature

  • All interactions available in DCore are supported.

  • [experimental] two-particle Green’s function

  • [todo] tail evaluation of Gf

Install

The following library/program needs to be installed:

How to use

Mandatory parameters:

[impurity_solver]
name = pomerol
exec_path{str} = /install_directory/bin/pomerol2dcore

Optional parameters:

n_bath{int} = 3  # 0 for default
fit_gtol{float} = 1e-6  # 1e-5 for default

The default value of n_bath is 0, namely, no bath site is taken into account (Hubbard-I approximation). For n_bath>0, hybridization function Delta(iw) is fitted by

\[\Delta^{n_\mathrm{bath}}_{o_1 o_2}(i\omega) = \sum_{l=1}^{n_\mathrm{bath}} \frac{V_{o_1 l} V_{l o_2}}{i\omega - \epsilon_l}\]

Then, the finite-size system consisting of the impurity site and n_bath bath sites are solve by ED method. The size of the Hilbert space increases exponentially according to \(2^{n_\textrm{spn-orb}}\) where \(n_\textrm{spn-orb}=2*n_\mathrm{orb} + 2*n_\mathrm{bath}\). Because of storage limitation, \(n_\textrm{spn-orb} \simeq 16\) is the limits in this solver.

Example

The square-lattice model in tutorial is solved by the pomerol solver using the following input parameter set:

dmft_square_pomerol.ini

[model]
seedname = square
lattice = square
norb = 1
nelec = 1.0
t = -1.0
kanamori = [(4.0, 0.0, 0.0)]
nk = 8

[system]
T = 0.1
n_iw = 1000
mu = 2.0
fix_mu = True

[impurity_solver]
name = pomerol
exec_path{str} = pomerol2dcore
n_bath{int} = 3
fit_gtol{float} = 1e-6

[control]
max_step = 100
sigma_mix = 0.5
time_reversal = True
converge_tol = 1e-5

[post.spectrum]
broadening = 0.4
knode = [(G,0.0,0.0,0.0),(X,0.5,0.0,0.0),(M,0.5,0.5,0.0),(G,0.0,0.0,0.0)]
nk_line = 100

[post.anacont]
omega_max =6.0
omega_min =-5.0
Nomega = 400

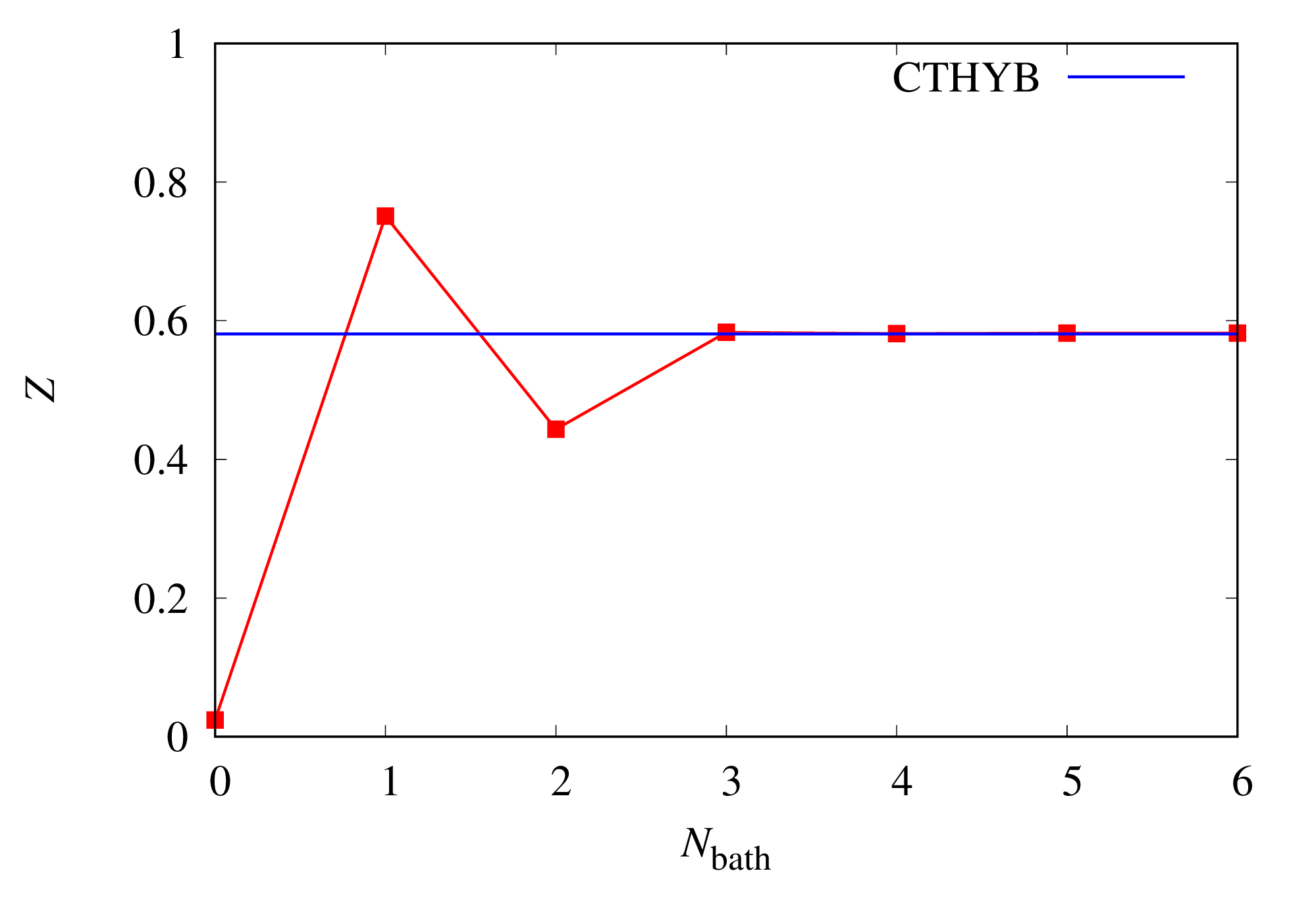
It is recommended to set convergence_tol parameter in [control] block to stop the DMFT loop automatically. The figure below shows the renormalization factor as a function of n_bath. Convergence to the CTHYB result is obtained around n_bath=3.

../../_images/renorm.png