7.2. チュートリアル

このチュートリアルでは, 正方格子ハバードモデル(8サイト)を例にとり説明する.

7.2.1. HPhi/vmc.out の実行

• \({\mathcal H}\Phi\) の場合

  基底状態および相関関数の計算を行う. 入力ファイルは次の通り.

  a0w = 2
  a0l = 2
  a1w = -2
  a1l = 2
  model="Hubbard"
  method="CG"
  lattice="square"
  t=1.0
  U=8.0
  nelec = 8
  2Sz=0
  

  $ HPhi -s input
  

• mVMC の場合

  まず変分波動関数の最適化を行う. 入力ファイルは次の通り.

  a0w = 2
  a0l = 2
  a1w = -2
  a1l = 2
  model="Hubbard"
  lattice="square"
  t=1.0
  U=8.0
  nelec = 8
  2Sz=0
  

  $ vmc.out -s input
  

  相関関数を計算するために, 入力ファイルに以下の行を付け加える.

  NVMCCalMode = 1
  

  相関関数を計算する.

  $ vmc.out -s input output/zqp_opt.dat
  

これにより, カレントディレクトリの output/ 以下に 1体および2体の相関関数が出力される.

関連するファイル

• StdFace.def (mVMC/\({\mathcal H}\Phi\) のマニュアル参照)

• zqp_opt.dat (mVMCのマニュアル参照)

• greenone.def (計算する相関関数のインデックスの指定)

• greentwo.def (計算する相関関数のインデックスの指定)

7.2.2. 相関関数のフーリエ変換

ユーティリティプログラム greenr2k を使って, 相関関数をフーリエ変関する.

$ echo "4 20
G 0 0 0
X 0.5 0 0
M 0.5 0.5 0
G 0 0 0
16 16 1" >> geometry.dat
$ greenr2k namelist.def geometry.dat

これにより, カレントディレクトリの output/ 以下に フーリエ変換された相関関数が出力される.

関連するファイル

• output/zvo_cisajs_001.dat (サイト表示の1体および2体相関関数の計算結果)

• output/zvo_cisajs.dat (サイト表示の1体および2体相関関数の計算結果)

• output/zvo_cisajscktalt_001.dat (サイト表示の1体および2体相関関数の計算結果)

• output/zvo_cisajscktalt.dat (サイト表示の1体および2体相関関数の計算結果)

• geometry.dat (サイトの位置と軌道のインデックス, k 点)

• output/zvo_corr*.dat (k パス上での相関関数)

7.2.3. 相関関数のプロット

gnuplotを使って, 相関関数を \(k\) 空間でプロットする.

load "kpath.gp"
plot "output/zvo_corr_eigen0.dat" u 1:12 w l

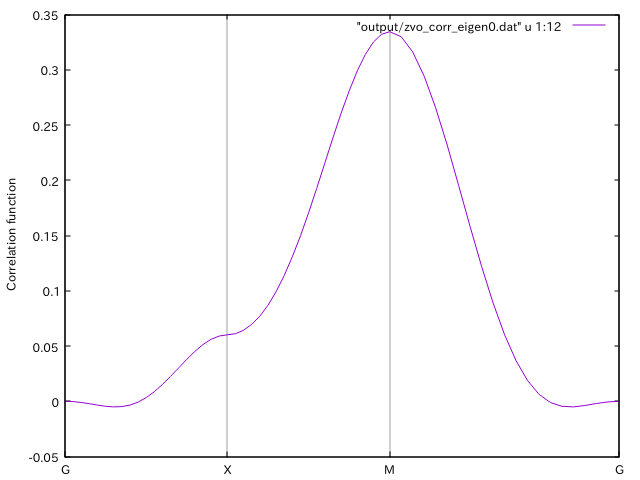
図 7.1 相関関数 \(\langle{\bf S}_{\bf k}\cdot{\bf S}_{\bf k}\rangle\) (12列目)を プロットした図.

関連するファイル

• kpath.gp (gnuplot スクリプト)

• output/zvo_corr*.dat (k パス上での相関関数)