Format of files

Input files

“Namelist” file

This file has four namelist (filename, ham, cg, dyn). For the details of the namelist of fortran, see some books and Web page for fortran.

&filename
  inham = ""
  invec = ""
/
&ham
nsite = 4
Jx = 1d0
Jy = 1d0
Jz = 1d0
Dz = 0d0
/
&cg
  maxloops = 100
  convfactor = 6
/
&dyn
  calctype = "normal"
  nomega = 100
  omegamin = (-2d0, 0.1d0)
  omegamax = ( 1d0, 0.1d0)
  outrestart = .TRUE.
/

In the namelist “filename”`, we specify the file names of the Hamiltonian and the RHS vector.

  • InHam

    Type : string (default: "")

    Description : The name of the file for the Hamiltonian in the MatrixMarket format (full path or relative path). If this parameter is not specified, the Hamiltonian of the 1D spin chain is generated with the parameters in ham namelist.

  • InVec

    Type : string (default: "")

    Description : The name of the file for the right hand side vector. If this parameter is not specified, the RHS vector is generated as follows: First the ground-state vector is computed. Then RHS vector is calculated by operating \({\hat S}_{1 z}\) (\(z\) component of the spin at site 1) to the ground-state vector. Therefore, we assume the computed system is the one-dimensional spin chain.

"ham" namelist is read only when

InHam is not specified. The parameters in this namelist are used to generate the Hamiltonian of the one-dimensional spin chain (See Fig. 2)

\[\begin{split}\begin{align} {\hat H} = \sum_{i} \left( \begin{matrix} {\hat S}_{i x} & {\hat S}_{i y} & {\hat S}_{i z} \end{matrix} \right) \left( \begin{matrix} J_x & D_z & 0 \\ -D_z & J_y & 0 \\ 0 & 0 & J_z \end{matrix} \right) \left( \begin{matrix} {\hat S}_{i+1 x} \ {\hat S}_{i+1 y} \ {\hat S}_{i+1 z} \end{matrix} \right). \end{align}\end{split}\]
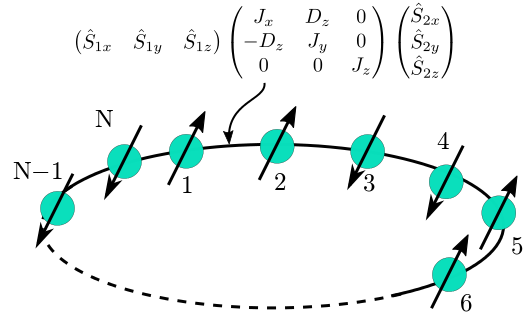
_images/spin.png

Figure 2: Schematic picture of the one-dimensional spin chain.

  • nsite

    Type : int (default: 4)

    Description : The number of sites in the 1D spin chain model.

  • Jx

    Type : double (default: 1.0)

    Description : \(J_x\) for the Heisenberg model.

  • Jy

    Type : double (default: 1.0)

    Description : \(J_y\) for the Heisenberg model.

  • Jz

    Type : double (default: 1.0)

    Description : \(J_z\) for the Heisenberg model.

  • Dz

    Type : double (default: 0.0)

    Description : The parameter of the Dzyaloshinskii-Moriya interaction (\(D_z\)).

cg namelist has parameters for specifying the numerical condition for the (Bi)Conjugate-gradient method.

  • MaxLoops

    Type : int (default: the dimension of the Hamiltonian)

    Description : The maximum number of iterations.

  • Convfactor

    Type : int (default: 8)

    Description : Convergence threshold. If the 2-norm of the residual vector becomes smaller than \(10^{-{\tt Convfactor}}\), the calculation finishes.

dyn has the parameters for the computation of the spectrum.

  • OmegaMin

    Type : Complex (default: If invec is not specified, the real part of it becomes the smallest eigenvalue, and the imaginary part of it becomes \(\times0.01\) times the difference between the largest- and the smallest- eigenvalue. If invec is specified, the default value becomes (0.0, 0.01))

    Description : The smallest frequency.

  • OmegaMax

    Type : Complex (default: If invec is not specified, the real part of it becomes the largest eigenvalue, and the imaginary part of it becomes \(\times0.01\) times the difference between the largest- and the smallest- eigenvalue. If invec is specified, the default value becomes (1.0, 0.01))

    Description : The largest frequency.

  • NOmega

    Type : int (default: 10)

    Description : The number of frequencies.

  • outrestart

    Type : Logical (default: .FALSE.)

    Description : Whether data for restart will be written (.TRUE.) or not (.FALSE.).

  • calctype

    Type : String. Choose from "normal", "recalc", "restart". (default: "normal")

    Description : "normal" for computing with the Krylov subspace from scratch. "recalc" for computing with the Krylov subspace generated in the previous calculation. In this case, the matrix-vector product is not performed. The convergence is not guaranteed. "restart" for restarting the calculation from the previous run. In this case, the calculation continues until the convergence is achieved or the number of iteration becomes MaxLoops.

“InHam” file

The Hamiltonian is written in the MatrixMarket format.

Example of the “InHam” file:

%%MatrixMarket matrix coordinate complex hermitian
16 16 20
1 1 1.000000 0.000000
3 2 0.500000 0.000000
5 3 0.500000 0.000000
6 4 0.500000 0.000000
6 6 -1.000000 0.000000
7 6 0.500000 0.000000
9 2 0.500000 0.000000
9 5 0.500000 0.000000
10 6 0.500000 0.000000
11 4 0.500000 0.000000
11 7 0.500000 0.000000
11 10 0.500000 0.000000
11 11 -1.000000 0.000000
12 8 0.500000 0.000000
13 6 0.500000 0.000000
13 11 0.500000 0.000000
14 12 0.500000 0.000000
15 8 0.500000 0.000000
15 14 0.500000 0.000000
16 16 1.000000 0.000000
First row:

Arbitrary string (such as comment).

Second row:

The number of rows, columns, and non-zero elements (in the lower triangle part).

Third row - End:

The row- and the column- index, and the real- and imaginary- part of the non-zero element (in the lower triangle part).

“InVec” file

Right hand side vector is contained.

Example of the “InVec” file:

8192
0.02 0.01
0.02 0.001
(continue...)

  • First row: [ int01 ]

    Type : int

    Description : The dimension of the Hilbert space. It must be the same as the dimension of the Hamiltonian.

  • Second row - End: [ double01 ] [ double02 ]

    Type : double

    Description : The element of the RHS vector. [ double01 ] is the real part, and [ double02 ] is the imaginary part.

Coefficients for restart

The coefficient \(\alpha\) and \(\beta\) are contained.

The name of the generated file is TriDiagComp.dat.

The example of this file:

1000
1.0 0.0
0.1 0 0.01  0
0.2 0 0.021 0
(continue...)
2.1 -0.5
3.1 4.0
(continue...)

  • First row: [ int01 ]

    Type : int

    Description : The length of \(\alpha, \beta\). It is the same as the number of iterations in the previous run.

  • Second row: [ double01 ] [ double02 ]

    Type : double

    Description : The seed frequency \(z_{\rm seed}\). [ double01 ] is the real part of \(z_{\rm seed}\), and [ double02 ] is the imaginary par of \(z_{\rm seed}\).

  • Third row - 2 + [ int01 ]th row: [ double03 ] [ double04 ] [ double05 ] [ double06 ]

    Type : double

    Description : \(\alpha, \beta\) at the each iteration. [ double03 ] is the real part of \(\alpha\), [ double04 ] is the imaginary part of \(\alpha\), [ double05 ] is the real part of \(\beta\), [ double06 ] is the imaginary part of \(\beta\).

  • 3 + [ int01 ]th row - 2 + \(2\times[\) int01 ]th row: [ double07 ] [ double08 ]

    Type : double

    Description : The product of the RHS vector and the residual vector at the each iteration. [ double07 ] is the real part of it, and [ double08 ] is the imaginary part of it.

Residual vector

The residual vector is contained for the restart. The file name is ResVec.dat.

Example of this file:

8192
0.02 0.01
0.02 0.001
(continue...)
0.02 0.01
0.02 0.001
(continue... Only for BiCG)

  • First row: [ int01 ]

    Type : int

    Description : The dimension of the Hilbert space.

  • Second row - 1 + [ int01 ]th row: [ double01 ] [ double02 ]

    Type : double

    Description : Each element of the residual vector. [ double01 ] is the real part of it, and [ double02 ] is the imaginary part of it.

  • Third row - 1 + 2 \(\times\) [ int01 ]th row: [ double03 ] [ double04 ]

    Type : double

    Description : (Only when the Hamiltonian is a complex matrix) Each element of the shadow residual vector. [ double03 ] is the real part of it, [ double04 ] is the imaginary part of it.

Output file

Coefficient for restart

The format is the same as Coefficients for restart.

Residual vector

The format is the same as Residual vector.

Dynamical Green’s function

The dynamical Green’s function is contained.

Example of this file:

-10 0.001 0.001 -0.0001
-9.8 0.001 0.0012 -0.0002
-9.6 0.001 0.0014 -0.0003
(continue...)

  • First row - END: [ double01 ] [ double02 ] [ double03 ] [ double04 ]

    • [ double01 ], [ double02 ]

      Type : double

      Description : The real- ([ double01 ]) and the imaginary- ([ double02 ]) part of the frequency.

    • [ double03 ], [ double04 ]

      Type : double

      Description : The dynamical Green’s function. [ double01 ] is the real part of it, and [ double02 ] is the imaginary part of it.