Optimization by replica exchange Monte Carlo¶
This tutorial describes how to estimate the minimization problem of Himmelblau function by using the replica exchange Monte Carlo method (RXMC).
Sample files¶
Sample files are available from sample/analytical/exchange .
This directory includes the following files:
input.tomlThe input file of odatse
do.shScript files for running this tutorial
Input files¶
This subsection describes the input file. For details, see the input file section of the manual.
[base]
dimension = 2
output_dir = "output"
[solver]
name = "analytical"
function_name = "himmelblau"
[algorithm]
name = "exchange"
seed = 12345
[algorithm.param]
min_list = [3.0, 3.0]
max_list = [6.0, 6.0]
step_list = [0.3, 0.3]
[algorithm.exchange]
Tmin = 0.01
Tmax = 100.0
numsteps = 10000
numsteps_exchange = 100
nreplica_per_proc = 20
In the following, we will briefly describe this input file. For details, see the manual of Replica exchange Monte Carlo exchange.
The contents of [base], [solver], and [runner] sections are the same as those for the search by the Nelder-Mead method (minsearch).
[algorithm] section specifies the algorithm to use and its settings.
nameis the name of the algorithm you want to use. In this tutorial we will use RXMC, so specifyexchange.seedis the seed that a pseudo-random number generator uses.
[algorithm.param] section sets the parameter space to be explored.
min_listis a lower bound andmax_listis an upper bound.unit_listis step length in one Monte Carlo update (deviation of Gaussian distribution).
[algorithm.exchange] section sets the hyper parameters for RXMC.
numstepis the number of Monte Carlo steps.numsteps_exchangeis the number of steps between temperature exchanges.Tmin,Tmaxare the minimum and the maximum of temperature, respectively.When
Tlogspaceistrue, the temperature points are distributed uniformly in the logarithmic space.nreplica_per_procspecifies the number of replicas that one MPI process handles.
Calculation¶
First, move to the folder where the sample file is located. (Hereinafter, it is assumed that you are the root directory of ODAT-SE.)
$ cd sample/analytical/exchange
Then, run the main program. It will take a few secondes on a normal PC.
$ mpiexec -np 4 python3 ../../../src/odatse_main.py input.toml | tee log.txt
Here, the calculation is performed using MPI parallel with 4 processes.
If you are using Open MPI and you request more processes than the number of cores, you need to add the --oversubscribe option to the mpiexec command.
When executed, a folder for each MPI rank will be created under output directory, and a trial.txt file containing the parameters evaluated in each Monte Carlo step and the value of the objective function, and a result.txt file containing the parameters actually adopted will be created.
These files have the same format: the first two columns are time (step) and the index of walker in the process, the third is the temperature, the fourth column is the value of the objective function, and the fifth and subsequent columns are the parameters.
# step walker T fx x1 x2
0 0 0.01 170.0 0.0 0.0
0 1 0.01123654800138751 187.94429125133564 5.155393113805774 -2.203493345018569
0 2 0.012626001098748564 3.179380982615041 -3.7929742598748666 -3.5452766573635235
0 3 0.014187266741165962 108.25464277273859 0.8127003489802398 1.1465364357510186
0 4 0.01594159037455999 483.84183395038843 5.57417423682746 1.8381251624588506
0 5 0.01791284454622004 0.43633134370869153 2.9868796504069426 1.8428384502208246
0 6 0.020127853758499396 719.7992581349758 2.972577711255287 5.535680832873856
0 7 0.022616759492228647 452.4691017123836 -5.899340424701358 -4.722667479627368
0 8 0.025413430367026365 45.5355817998709 -2.4155554347674215 1.8769341969872393
0 9 0.028555923019901074 330.7972369561986 3.717750630491217 4.466110964691396
0 10 0.032086999973704504 552.0479484091458 5.575771168463163 2.684224163039442
...
best_result.txt is filled with information about the parameter with the optimal objective function, the rank from which it was obtained, and the Monte Carlo step.
nprocs = 80
rank = 3
step = 8025
walker = 17
fx = 3.358076734724385e-06
x1 = 2.9998063442504126
x2 = 1.999754886043102
In ODAT-SE, one replica holds samples at different temperatures because of the temperature exchanges. The result.txt in each rank folder records the data sampled by each replica.
The data reorganized for each temperature point is written to output/result_T%.txt, where % is the index of the temperature point.
The first column is the step, the second column is the rank, the third column is the value of the objective function, and the fourth and subsequent columns are the parameters.
Example:
# T = 0.014187266741165962
0 3 108.25464277273859 0.8127003489802398 1.1465364357510186
1 3 108.25464277273859 0.8127003489802398 1.1465364357510186
2 3 108.25464277273859 0.8127003489802398 1.1465364357510186
3 3 108.25464277273859 0.8127003489802398 1.1465364357510186
4 3 93.5034551820852 1.3377081691728905 0.8736706475438123
5 3 81.40963740872147 1.4541906604820898 1.0420053981467825
...
Visualization¶
By plotting output/result_T%.txt, you can estimate regions where the parameters with small function values are located.
By executing the following command, the figures of two-dimensional plot res_T%.png will be generated.
$ python3 ../plot_himmel.py --xcol=3 --ycol=4 --skip=20 --format="o" --output=output/res_T0.png output/result_T0.txt
Looking at the resulting diagram, we can see that the samples are concentrated near the minima of f(x). By changing the index of the temperature, the sampling points scatters over the region at high temperature, while they tend to concentrate on the minima at low temperature.
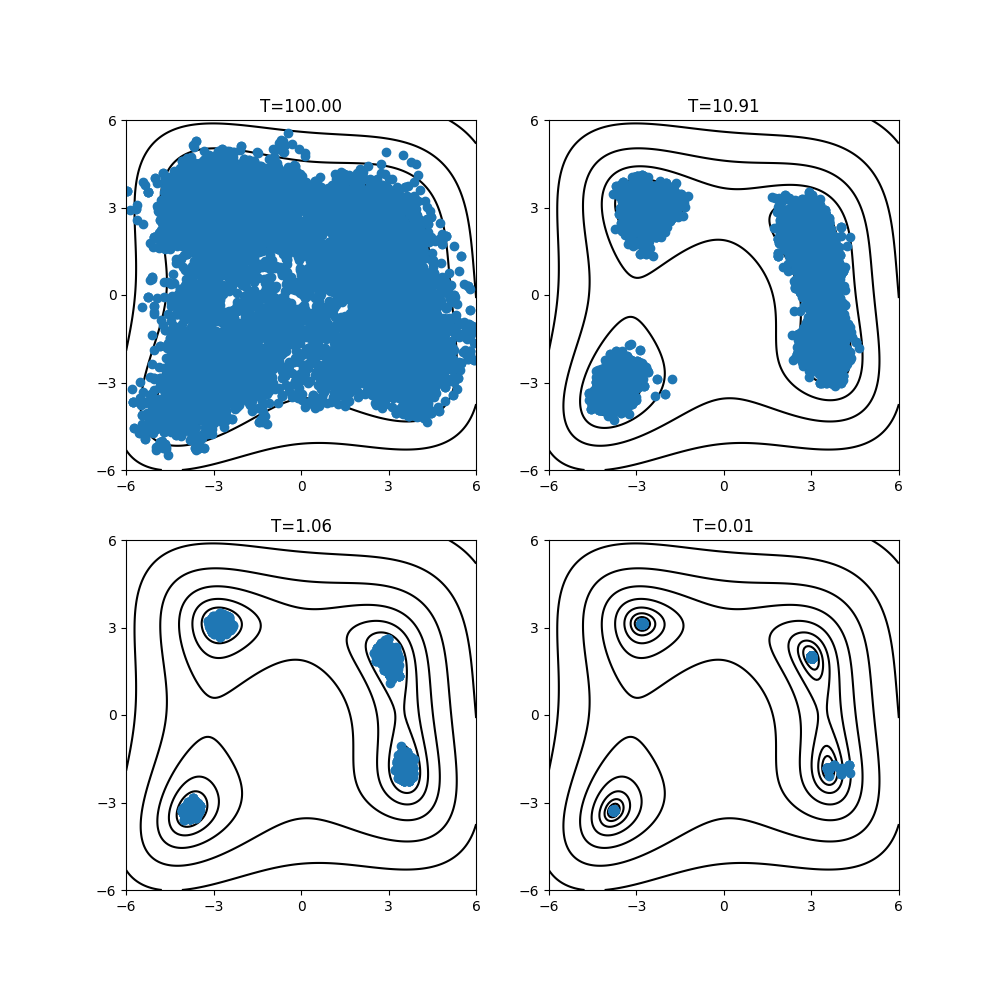
Fig. 6 Distribution of sampling points on two-dimensional parameter space at \(T=\{35.02, 3.40, 0.33, 0.01\}\).¶