Minimization of an analytical function

As an example of direct problem solver, the minimization of Himmelblau function among the Analytical solver included in ODAT-SE will be discussed in these tutorials. The Himmelblau function is a two-variable function given as follows, having multiple number of minima. It is used as a benchmark for the evaluation of optimization algorithms.

\[f(x,y) = (x^2+y-11)^2 + (x+y^2-7)^2\]

The minimum value \(f(x,y)=0\) is given at \((x,y)\) that equals to \((3.0, 2.0)\), \((-2.805118, 3.131312)\), \((-3.779310, -3.283186)\), and \((3.584428, -1.848126)\).

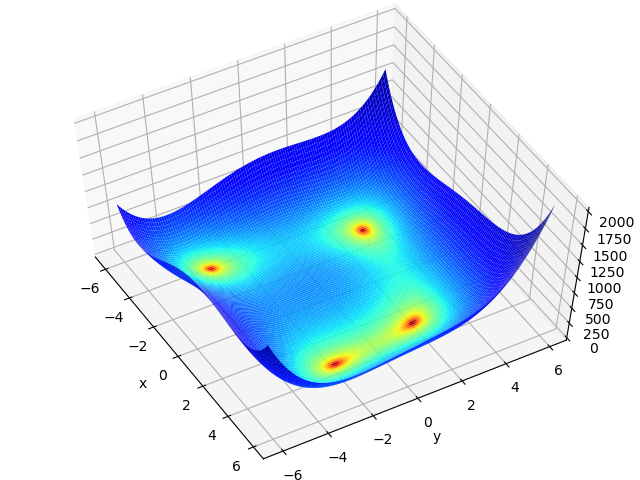
Fig. 1 The plot of Himmelblau function.

[1] D. Himmelblau, Applied Nonlinear Programming, McGraw-Hill, 1972.