Optimization by Nelder-Mead method¶
In this section, we will explain how to calculate the minimization problem of Himmelblau function using the Nelder-Mead method. The specific calculation procedure is as follows.
Preparation of an input file
Prepare an input file that describes parameters in TOML format.
Run the main program
Run the calculation using
src/odatse_main.pyto solve the minimization problem.
Location of the sample files¶
The sample files are located in sample/analytical/minsearch.
The following files are stored in the folder.
input.tomlInput file of the main program.
do.shScript prepared for doing all calculation of this tutorial
In addition, plot_himmel.py in the sample folder is used to visualize the result.
Input file¶
In this section, we will prepare the input file input.toml for the main program.
The details of input.toml can be found in the input file section of the manual.
[base]
dimension = 2
output_dir = "output"
[solver]
name = "analytical"
function_name = "himmelblau"
[runner]
[runner.log]
interval = 20
[algorithm]
name = "minsearch"
seed = 12345
[algorithm.param]
min_list = [-6.0, -6.0]
max_list = [ 6.0, 6.0]
initial_list = [0, 0]
[base] section describes parameters used in the whole program.
dimensionis the number of variables to be optimized, in this case2since Himmelblau function is a two-variable function.output_diris the name of directory for output.
[solver] section specifies the solver to be used inside the main program and its settings.
nameis the name of the solver you want to use. In this tutorial, we perform analyses of an analytical function in theanalyticalsolver.function_nameis the name of the function in theanalyticalsolver.
[runner] section specifies settings on calling the direct problem solver from the inverse problem analysis algorithm.
intervalin[runner.log]specifies the frequency of the log output. The logs are written in everyintervalsteps.
[algorithm] section specifies the algorithm to use and its settings.
nameis the name of the algorithm you want to use. In this tutorial we will useminsearchsince we will be using the Nelder-Mead method.seedspecifies the initial input of random number generator.
[algorithm.param] section specifies the range of parameters to search and their initial values.
min_listandmax_listspecify the minimum and maximum values of the search range, respectively.initial_listspecifies the initial values.
Other parameters, such as convergence judgments used in the Nelder-Mead method, can be done in the [algorithm] section, although they are omitted here because the default values are used.
See the input file chapter for details.
Calculation execution¶
First, move to the folder where the sample files are located. (We assume that you are directly under the directory where you downloaded this software.)
$ cd sample/analytical/minsearch
Then, run the main program. The computation time takes only a few seconds on a normal PC.
$ python3 ../../../src/odatse_main.py input.toml | tee log.txt
The standard output will be seen as follows.
Optimization terminated successfully.
Current function value: 0.000000
Iterations: 40
Function evaluations: 79
iteration: 40
len(allvecs): 41
step: 0
allvecs[step]: [0. 0.]
step: 1
allvecs[step]: [0.375 0.375]
step: 2
allvecs[step]: [0.0625 0.9375]
step: 3
allvecs[step]: [0.65625 1.46875]
step: 4
allvecs[step]: [0.328125 2.859375]
...
The x1 and x2 are the candidate parameters at each step and the function value at that point.
The final estimated parameters is written to output/res.dat.
In the current case, the following result will be obtained:
fx = 4.2278370361994904e-08
x1 = 2.9999669562950175
x2 = 1.9999973389336225
It is seen that one of the minima is obtained.
Visualization of calculation results¶
The steps taken during the search by the Nelder-Mead method is written in output/0/SimplexData.txt. A tool to plot the path is prepared as simplex/plot_himmel.py.
$ python3 ../plot_himmel.py --xcol=1 --ycol=2 --output=output/res.pdf output/0/SimplexData.txt
By executing the above command, output/res.pdf will be generated.
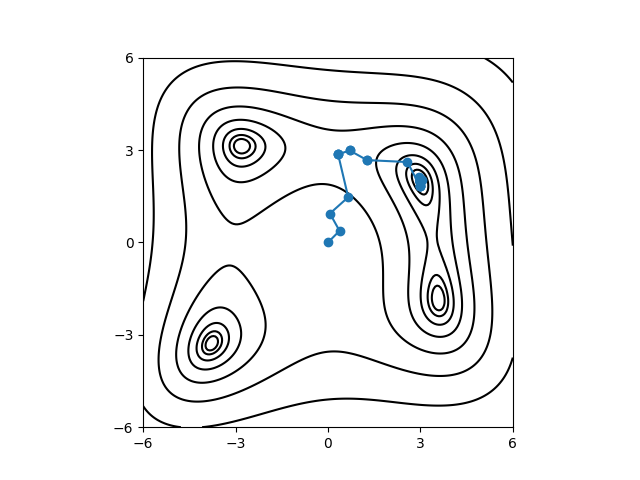
Fig. 2 The path taken during the minimum search by the Nelder-Mead method is drawn by the blue line. The black curves show contour of Himmelblau function.¶
The path of the minimum search by the Nelder-Mead method is drawn on top of the contour plot of Himmelblau function. Starting from the initial value at (0, 0), the path reaches to one of the minima, (3, 2).