ベイズ最適化¶
ここでは、ベイズ最適化を行いて Himmelblau関数の最小化問題を解析する方法について説明します。 ベイズ最適化には PHYSBO を用います。 事前に PHYSBO パッケージをインストールしておきます。
サンプルファイルの場所¶
サンプルファイルは sample/analytical/bayes にあります。
フォルダには以下のファイルが格納されています。
input.tomlメインプログラムの入力ファイル
do.sh本チュートリアルを一括計算するために準備されたスクリプト
また、計算結果を可視化するために sample フォルダ内の plot_himmel.py を利用します。
入力ファイルの説明¶
メインプログラム用の入力ファイル input.toml を作成します。記述方法の詳細については「入力ファイル」の項を参照してください。
[base]
dimension = 2
output_dir = "output"
[solver]
name = "analytical"
function_name = "himmelblau"
[algorithm]
name = "bayes"
seed = 12345
[algorithm.param]
min_list = [-6.0, -6.0]
max_list = [ 6.0, 6.0]
num_list = [61, 61]
[algorithm.bayes]
random_max_num_probes = 20
bayes_max_num_probes = 40
[base], [solver], [runner] のセクションについては Nelder-Mead法による探索(minsearch)の場合と同じです。
[algorithm] セクションでは、使用するアルゴリスムとその設定をします。
nameは使用するアルゴリズムの名前です。このチュートリアルでは、ベイズ最適化を用いた解析を行うので、bayesを指定します。seedは乱数の初期値を指定します。
[algorithm.param] セクションでは、探索するパラメータの範囲や初期値を指定します。
min_listとmax_listはそれぞれ探索範囲の最小値と最大値を指定します。num_listはパラメータの各方向へのグリッド点の個数を指定します。
[algorithm.bayes] セクションでは、ベイズ最適化に関するハイパーパラメータを指定します。
random_max_num_probesはランダムサンプリングの回数を指定します。bayes_max_num_probesはベイズ最適化を行う回数を指定します。
ここではデフォルト値を用いるため省略しましたが、その他のパラメータについて詳細は「入力ファイル」の章を参照してください。
計算の実行¶
最初にサンプルファイルが置いてあるフォルダへ移動します。(以下、ODAT-SEパッケージをダウンロードしたディレクトリ直下にいることを仮定します。)
$ cd sample/analytical/bayes
メインプログラムを実行します。計算時間は通常のPCで数秒程度で終わります。
$ python3 ../../../src/odatse_main.py input.toml | tee log.txt
実行すると output ディレクトリの下に各ランクのフォルダが作成されます。
以下の様な標準出力がされます。
# parameter
random_max_num_probes = 10
bayes_max_num_probes = 20
score = TS
interval = 5
num_rand_basis = 5000
value_01 = 5.10000
value_02 = 4.90000
R-factor = 0.037237314010261195
0001-th step: f(x) = -0.037237 (action=150)
current best f(x) = -0.037237 (best action=150)
value_01 = 4.30000
value_02 = 3.50000
...
最初に設定したパラメータのリスト、そのあとに各ステップでの候補パラメータと、
その時の関数値 f(x) が出力されます。
また、その時点での一番良いスコアを持つグリッドインデックス (action)とその場合の f(x) と変数が出力されます。
最終的に推定されたパラメータは、 output/BayesData.txt に出力されます。
今回の場合は
#step x1 x2 fx x1_action x2_action fx_action
0 -2.4 -0.7999999999999998 113.2192 -2.4 -0.7999999999999998 113.2192
1 -2.4 -0.7999999999999998 113.2192 1.6000000000000005 4.600000000000001 263.12320000000045
2 2.8000000000000007 -0.39999999999999947 28.995199999999958 2.8000000000000007 -0.39999999999999947 28.995199999999958
3 2.8000000000000007 -0.39999999999999947 28.995199999999958 4.800000000000001 5.800000000000001 1306.739200000001
4 2.8000000000000007 -0.39999999999999947 28.995199999999958 -1.3999999999999995 2.5999999999999996 44.16320000000003
5 2.8000000000000007 -0.39999999999999947 28.995199999999958 2.200000000000001 -5.2 623.6672
6 2.8000000000000007 -0.39999999999999947 28.995199999999958 -1.1999999999999993 2.200000000000001 65.45919999999997
7 4.200000000000001 -1.7999999999999998 23.619200000000067 4.200000000000001 -1.7999999999999998 23.619200000000067
8 4.200000000000001 -1.7999999999999998 23.619200000000067 -2.5999999999999996 -0.1999999999999993 111.10720000000002
9 4.200000000000001 -1.7999999999999998 23.619200000000067 0.6000000000000005 0.8000000000000007 130.00319999999994
10 4.200000000000001 -1.7999999999999998 23.619200000000067 -0.5999999999999996 -0.5999999999999996 178.7552
...
38 3.200000000000001 1.8000000000000007 1.3952000000000133 3.200000000000001 -1.3999999999999995 8.051199999999973
39 3.200000000000001 1.8000000000000007 1.3952000000000133 -3.8 -3.0 3.433599999999999
40 3.200000000000001 1.8000000000000007 1.3952000000000133 -3.0 -2.8 27.705600000000004
41 3.6000000000000014 -1.7999999999999998 0.051200000000003215 3.6000000000000014 -1.7999999999999998 0.051200000000003215
42 3.6000000000000014 -1.7999999999999998 0.051200000000003215 2.0 2.5999999999999996 22.457599999999996
...
のように得られます。1列目にステップ数、2〜4列目にその時点での最高スコアを与える x1, x2 と f(x) が記載されます。
続けて、そのステップで候補となった x1, x2 と f(x) が記載されます。
今回の場合は41ステップ目で正しい解が得られていることがわかります。
計算結果の可視化¶
output/BayesData.txt を参照すると、何ステップ目のパラメータが最小スコアを与えたかがわかります。
$ python3 ../plot_himmel.py --xcol=1 --ycol=2 --format="-o" --output=output/res.pdf output/BayesData.txt
$ python3 ../plot_himmel.py --xcol=4 --ycol=5 --format="o" --output=output/actions.pdf output/BayesData.txt
上記を実行すると output/actions.pdf と output/res.pdf が作成され、Himmelblau関数の関数値を表す等高線の上に、ベイズ最適化で評価したグリッド点と最小スコアを与える点の履歴がプロットされます。
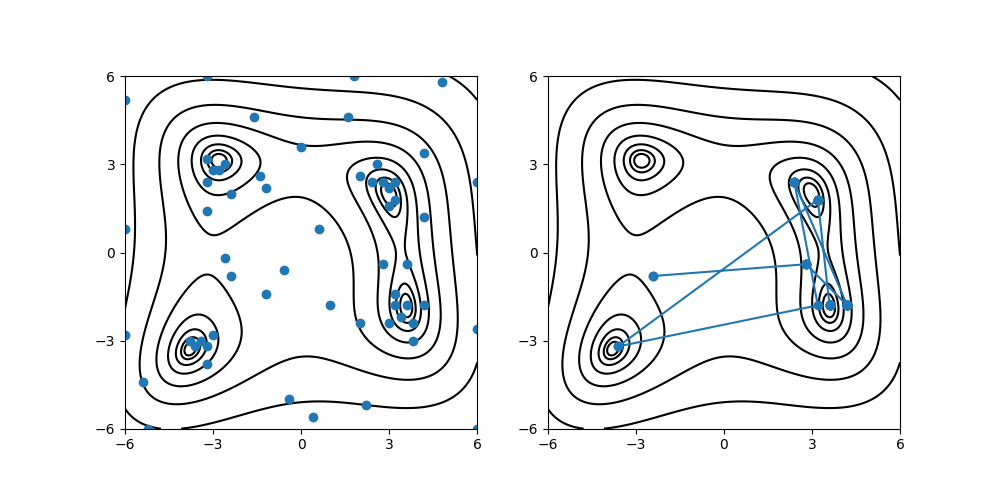
ベイズ最適化で評価したグリッド点(左図)と最小スコアを与える点の履歴(右図)¶