レプリカ交換モンテカルロ法による探索¶
ここでは、レプリカ交換モンテカルロ法を用いて Himmelblau関数の最小化問題を解析する方法について説明します。
具体的な計算手順は minsearch の時と同様です。
サンプルファイルの場所¶
サンプルファイルは sample/analytical/exchange にあります。
フォルダには以下のファイルが格納されています。
input.tomlメインプログラムの入力ファイル
do.sh本チュートリアルを一括計算するために準備されたスクリプト
入力ファイルの説明¶
メインプログラム用の入力ファイル input.toml について説明します。記述方法の詳細については「入力ファイル」の項を参照してください。
[base]
dimension = 2
output_dir = "output"
[solver]
name = "analytical"
function_name = "himmelblau"
[algorithm]
name = "exchange"
seed = 12345
[algorithm.param]
min_list = [3.0, 3.0]
max_list = [6.0, 6.0]
step_list = [0.3, 0.3]
[algorithm.exchange]
Tmin = 0.01
Tmax = 100.0
numsteps = 10000
numsteps_exchange = 100
nreplica_per_proc = 20
ここではこの入力ファイルを簡単に説明します。 詳細は入力ファイルのレファレンスを参照してください。
[base], [solver], [runner] のセクションについては Nelder-Mead法による探索(minsearch)の場合と同じです。
[algorithm] セクションでは、使用するアルゴリスムとその設定を行います。
nameは使用するアルゴリズムの名前です。このチュートリアルではレプリカ交換モンテカルロ法による解析を行うので、exchangeを指定します。
[algorithm.param] セクションでは、探索する連続なパラメータ空間の設定を行います。
min_listとmax_listはそれぞれ探索範囲の最小値と最大値を指定します。step_listはモンテカルロ更新の際の変化幅(ガウス分布の偏差)です。
[algorithm.exchange] サブセクションは、レプリカ交換モンテカルロ法のハイパーパラメータを指定します。
numstepはモンテカルロ更新の回数です。numsteps_exchangeで指定した回数のモンテカルロ更新の後に、温度交換を試みます。Tmin,Tmaxはそれぞれ温度の下限・上限です。Tlogspaceがtrueの場合、温度を対数空間で等分割します。nreplica_per_procは 1つのMPIプロセスが受け持つレプリカの数を指定します。
計算の実行¶
最初にサンプルファイルが置いてあるフォルダへ移動します。(以下、ODAT-SEパッケージをダウンロードしたディレクトリ直下にいることを仮定します。)
$ cd sample/analytical/exchange
メインプログラムを実行します。計算時間は通常のPCで数秒程度で終わります。
$ mpiexec -np 4 python3 ../../../src/odatse_main.py input.toml | tee log.txt
ここではプロセス数4のMPI並列を用いた計算を行っています。
OpenMPI を用いる場合で、使えるコア数よりも要求プロセス数の方が多い時には、 mpiexec コマンドに --oversubscribe オプションを追加してください。
実行すると、 output ディレクトリの下に各ランクのフォルダが作成され、各モンテカルロステップで評価したパラメータおよび目的関数の値を記した trial.txt ファイルと、実際に採択されたパラメータを記した result.txt ファイルが作成されます。
ともに書式は同じで、最初の2列がステップ数とプロセス内のwalker 番号、次が温度、3列目が目的関数の値、4列目以降がパラメータです。
# step walker T fx x1 x2
0 0 0.01 170.0 0.0 0.0
0 1 0.01123654800138751 187.94429125133564 5.155393113805774 -2.203493345018569
0 2 0.012626001098748564 3.179380982615041 -3.7929742598748666 -3.5452766573635235
0 3 0.014187266741165962 108.25464277273859 0.8127003489802398 1.1465364357510186
0 4 0.01594159037455999 483.84183395038843 5.57417423682746 1.8381251624588506
0 5 0.01791284454622004 0.43633134370869153 2.9868796504069426 1.8428384502208246
0 6 0.020127853758499396 719.7992581349758 2.972577711255287 5.535680832873856
0 7 0.022616759492228647 452.4691017123836 -5.899340424701358 -4.722667479627368
0 8 0.025413430367026365 45.5355817998709 -2.4155554347674215 1.8769341969872393
0 9 0.028555923019901074 330.7972369561986 3.717750630491217 4.466110964691396
0 10 0.032086999973704504 552.0479484091458 5.575771168463163 2.684224163039442
...
best_result.txt に、目的関数が最小となったパラメータとそれを得たランク、モンテカルロステップの情報が書き込まれます。
nprocs = 80
rank = 3
step = 8025
walker = 17
fx = 3.358076734724385e-06
x1 = 2.9998063442504126
x2 = 1.999754886043102
ODAT-SE の実装では1つのレプリカが様々な温度のサンプルを保持しています。各ランクフォルダにある result.txt には、各レプリカでサンプリングされたデータが記録されています。
この全レプリカの結果から温度ごとのサンプルに整列し直したデータが output/result_T%.txt に出力されます。(% は温度点のindex。)
1列目がステップ、2列めがランク、3列目が目的関数の値、4列目以降がパラメータです。
# T = 0.014187266741165962
0 3 108.25464277273859 0.8127003489802398 1.1465364357510186
1 3 108.25464277273859 0.8127003489802398 1.1465364357510186
2 3 108.25464277273859 0.8127003489802398 1.1465364357510186
3 3 108.25464277273859 0.8127003489802398 1.1465364357510186
4 3 93.5034551820852 1.3377081691728905 0.8736706475438123
5 3 81.40963740872147 1.4541906604820898 1.0420053981467825
...
計算結果の可視化¶
result_T%.txt を図示することで f(x) の小さいパラメータがどこにあるかを推定することができます。
以下のコマンドを入力すると 2次元パラメータ空間の図 res_T%.png が作成されます。
$ python3 ../plot_himmel.py --xcol=3 --ycol=4 --skip=20 --format="o" --output=output/res_T0.png output/result_T0.txt
作成された図を見ると、 f(x) の最小値を与える点の付近にサンプルが集中していることが分かります。温度Tのインデックスを変えると、高温ではサンプリング点が領域内に広く分布していること、温度を下げると極小点付近に集中することが見てとれます。
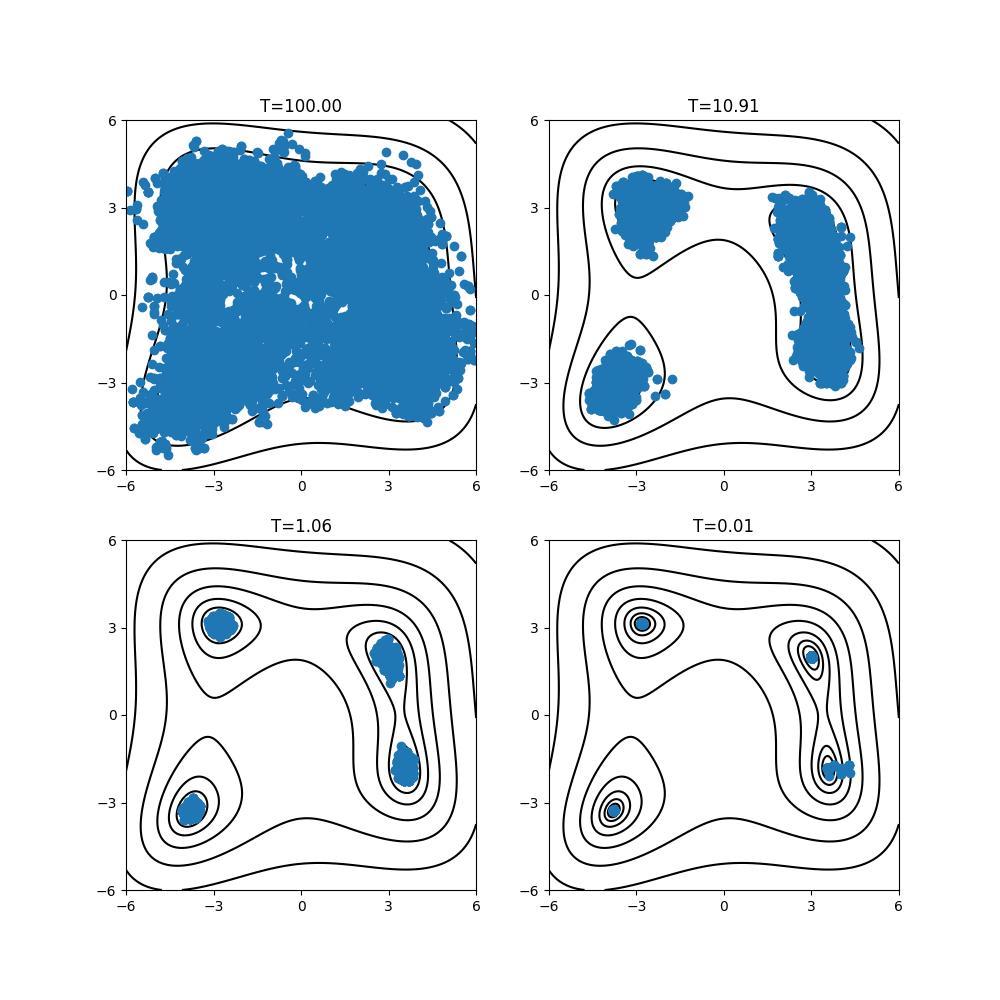
2次元パラメータ空間上のモンテカルロ法によるサンプリング点の分布。 \(T=\{35.02, 3.40, 0.33, 0.01\}\) の場合。¶