Nelder-Mead法による最適化¶
ここでは、Nelder-Mead法を用いて Himmelblau関数の最小値を探索する方法について説明します。 具体的な計算手順は以下の通りです。
入力ファイルを用意する
入力パラメータをTOML形式で記述した入力ファイルを作成します。
メインプログラムを実行する
src/odatse_main.pyを用いて計算を実行し、最適化問題を解きます。
サンプルファイルの場所¶
サンプルファイルは sample/analytical/minsearch にあります。
フォルダには以下のファイルが格納されています。
input.tomlメインプログラムの入力ファイル
do.sh本チュートリアルを一括計算するために準備されたスクリプト
また、計算結果を可視化するために sample フォルダ内の plot_himmel.py を利用します。
入力ファイルの説明¶
メインプログラム用の入力ファイル input.toml を作成します。記述方法の詳細については「入力ファイル」の項を参照してください。
[base]
dimension = 2
output_dir = "output"
[solver]
name = "analytical"
function_name = "himmelblau"
[runner]
[runner.log]
interval = 20
[algorithm]
name = "minsearch"
seed = 12345
[algorithm.param]
min_list = [-6.0, -6.0]
max_list = [ 6.0, 6.0]
initial_list = [0, 0]
[base] セクションではプログラム全体で利用するパラメータを設定します。
dimensionは最適化したい変数の個数です。Himmelblau関数は 2変数関数ですので、今の場合は2を指定します。output_dirは出力先のディレクトリを指定します。
[solver] セクションではメインプログラムの内部で使用するソルバーとその設定を指定します。
nameは使用するソルバーの名前です。このチュートリアルではanalyticalソルバーに含まれる解析関数の解析を行います。function_nameはanalyticalソルバー内の関数名を指定します。
[runner] セクションでは、逆問題解析アルゴリズムからソルバーの呼び出しに関する設定を行います。
[runner.log]のintervalは、ログ出力の頻度を指定します。interval回の繰り返し毎にログを出力します。
[algorithm] セクションでは、使用するアルゴリスムとその設定をします。
nameは使用するアルゴリズムの名前です。このチュートリアルでは、Nelder-Mead法 を用いた解析を行うので、minsearchを指定します。seedは乱数の初期値を指定します。
[algorithm.param] セクションでは、探索するパラメータの範囲や初期値を指定します。
min_listとmax_listはそれぞれ探索範囲の最小値と最大値を指定します。initial_listは初期値を指定します。
ここではデフォルト値を用いるため省略しましたが、その他のパラメータ、例えばNelder-Mead法で使用する収束判定などについては、[algorithm] セクションで行うことが可能です。
詳細については「入力ファイル」の章を参照してください。
計算の実行¶
最初にサンプルファイルが置いてあるフォルダへ移動します。(以下では、ODAT-SE パッケージをダウンロードしたディレクトリの直下にいることを仮定します。)
$ cd sample/analytical/minsearch
メインプログラムを実行します。計算時間は通常のPCで数秒程度で終わります。
$ python3 ../../../src/odatse_main.py input.toml | tee log.txt
実行すると、以下の様な出力がされます。
Optimization terminated successfully.
Current function value: 0.000000
Iterations: 40
Function evaluations: 79
iteration: 40
len(allvecs): 41
step: 0
allvecs[step]: [0. 0.]
step: 1
allvecs[step]: [0.375 0.375]
step: 2
allvecs[step]: [0.0625 0.9375]
step: 3
allvecs[step]: [0.65625 1.46875]
step: 4
allvecs[step]: [0.328125 2.859375]
...
x1, x2 に各ステップでの候補パラメータと、その時の関数値が出力されます。
最終的に推定されたパラメータは output/res.dat に出力されます。今の場合、
fx = 4.2278370361994904e-08
x1 = 2.9999669562950175
x2 = 1.9999973389336225
が得られ、最小値を与える解の一つが求められたことが分かります。
計算結果の可視化¶
Nelder-Mead法による解の探索の経路は output/0/SimplexData.txt に出力されています。
これをプロットするツールが sample/plot_himmel.py に用意されています。
$ python3 ../plot_himmel.py --xcol=1 --ycol=2 --output=output/res.pdf output/0/SimplexData.txt
上記を実行すると output/res.pdf が出力されます。
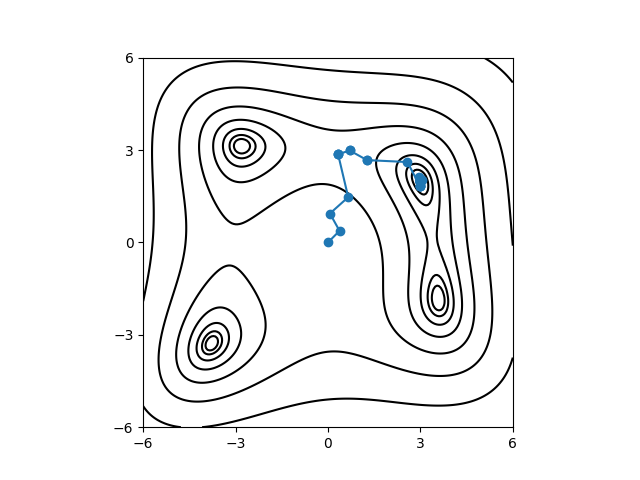
Nelder-Mead法を用いた Himmelblau 関数の最小値探索。黒線は Himmelblau関数の関数値を表す等高線、青色のシンボルは探索経路。¶
Himmelblau関数の関数値を表す等高線の上に Nelder-Mead法による探索の経路がプロットされます。初期値 (0, 0) からスタートして最小値を与える解の一つ (3, 2) に到達していることが分かります。