ポピュレーションアニーリングによる探索¶
ここでは、ポピュレーションアニーリングを用いて Himmelblau関数の最小化問題を解析する方法について説明します。
具体的な計算手順は minsearch の時と同様です。
サンプルファイルの場所¶
サンプルファイルは sample/analytical/pamc にあります。
フォルダには以下のファイルが格納されています。
input.tomlメインプログラムの入力ファイル
do.sh本チュートリアルを一括計算するために準備されたスクリプト
入力ファイルの説明¶
メインプログラム用の入力ファイル input.toml について説明します。記述方法の詳細については「入力ファイル」の項を参照してください。
[base]
dimension = 2
output_dir = "output"
[solver]
name = "analytical"
function_name = "himmelblau"
[runner]
[runner.log]
interval = 20
[algorithm]
name = "pamc"
seed = 12345
[algorithm.param]
max_list = [6.0, 6.0]
min_list = [-6.0, -6.0]
step_list = [0.1, 0.1]
[algorithm.pamc]
Tmin = 1.0
Tmax = 100.0
Tnum = 21
Tlogspace = true
numsteps_annealing = 100
nreplica_per_proc = 100
ここではこの入力ファイルを簡単に説明します。 詳細は入力ファイルのレファレンスを参照してください。
[base], [solver], [runner] のセクションについては Nelder-Mead法による探索(minsearch)の場合と同じです。
[algorithm] セクションでは、使用するアルゴリスムとその設定を行います。
nameは使用するアルゴリズムの名前です。このチュートリアルでは、ポピュレーションアニーリング法による解析を行うので、pamcを指定します。
[algorithm.param] セクションでは、探索する連続なパラメータ空間の設定を行います。
min_listとmax_listはそれぞれ探索範囲の最小値と最大値を指定します。step_listはモンテカルロ更新の際の変化幅(ガウス分布の偏差)です。
[algorithm.pamc] セクションは、ポピュレーションアニーリングのハイパーパラメータを指定します。
numsteps_annealingで指定した回数のモンテカルロ更新の後に、逆温度を増やします (温度を下げます)。bmin,bmaxはそれぞれ逆温度の下限・上限です。Tnumは計算する温度・逆温度の点数です。Tlogspaceがtrueの場合、温度を対数空間で等分割しますnreplica_per_procはMPIプロセスひとつが受け持つ計算レプリカの数です。
計算の実行¶
最初にサンプルファイルが置いてあるフォルダへ移動します。(以下、本ソフトウェアをダウンロードしたディレクトリ直下にいることを仮定します。)
$ cd sample/analytical/pamc
メインプログラムを実行します。計算時間は通常のPCで数秒程度で終わります。
$ mpiexec -np 4 python3 ../../../src/odatse_main.py input.toml | tee log.txt
ここではプロセス数4のMPI並列を用いた計算を行っています。
OpenMPI を用いる場合で、使えるコア数よりも要求プロセス数の方が多い時には、 mpiexec コマンドに --oversubscribe オプションを追加してください。
実行すると、 output ディレクトリの下に各ランクのフォルダが作成され、温度ごとに、各モンテカルロステップで評価したパラメータおよび目的関数の値を記した trial_TXXX.txt ファイル(XXX は温度点の番号)と、実際に採択されたパラメータを記した result_TXXX.txt ファイル、さらにそれぞれを結合した trial.txt, result.txt ファイルが生成されます。
それぞれ書式は同じで、最初の2列がステップ数とプロセス内の walker (replica) 番号、次が(逆)温度、3列目が目的関数の値、4列目以降がパラメータです。
最後の2 列は、 walker の重み (Neal-Jarzynski weight) と祖先(計算を開始したときのレプリカ)の番号です。
# step walker T fx x1 x2 weight ancestor
0 0 100.0 187.94429125133564 5.155393113805774 -2.203493345018569 1.0 0
0 1 100.0 3.179380982615041 -3.7929742598748666 -3.5452766573635235 1.0 1
0 2 100.0 108.25464277273859 0.8127003489802398 1.1465364357510186 1.0 2
0 3 100.0 483.84183395038843 5.57417423682746 1.8381251624588506 1.0 3
0 4 100.0 0.43633134370869153 2.9868796504069426 1.8428384502208246 1.0 4
0 5 100.0 719.7992581349758 2.972577711255287 5.535680832873856 1.0 5
0 6 100.0 452.4691017123836 -5.899340424701358 -4.722667479627368 1.0 6
0 7 100.0 45.5355817998709 -2.4155554347674215 1.8769341969872393 1.0 7
0 8 100.0 330.7972369561986 3.717750630491217 4.466110964691396 1.0 8
0 9 100.0 552.0479484091458 5.575771168463163 2.684224163039442 1.0 9
0 10 100.0 32.20027165958588 1.7097039347500953 2.609443449748964 1.0 10
...
output/best_result.txt に、目的関数が最小となったパラメータとそれを得たランク、モンテカルロステップの情報が書き込まれます。
nprocs = 4
rank = 3
step = 1806
walker = 74
fx = 4.748689609377718e-06
x1 = -2.805353724219707
x2 = 3.131045687296453
最後に、 output/fx.txt には、各温度ごとの統計情報が記録されます。
# $1: 1/T
# $2: mean of f(x)
# $3: standard error of f(x)
# $4: number of replicas
# $5: log(Z/Z0)
# $6: acceptance ratio
0.01 130.39908953806298 6.023477428315198 400 0.0 0.9378
0.01258925411794167 83.6274790817115 3.83620542622489 400 -0.2971072297035158 0.930325
0.015848931924611134 60.25390522675298 2.73578884504734 400 -0.5426399088244793 0.940375
0.01995262314968879 47.20146188151557 2.3479083531465976 400 -0.7680892360649545 0.93715
0.025118864315095794 41.118822390166315 1.8214854089575818 400 -0.9862114670289625 0.9153
...
1列目は温度・逆温度で、2・3列目は目的関数 \(f(x)\) の期待値と標準誤差、4列目はレプリカの個数、5列目は分配関数の比の対数 \(\log(Z_n/Z_0)\) (\(Z_0\) は最初の温度点における分配関数)、6列目はモンテカルロ更新の採択率です。
計算結果の可視化¶
result_T%.txt を図示することで f(x) の小さいパラメータがどこにあるかを推定することができます。
以下のコマンドを入力すると2次元パラメータ空間の図 res_T%.png が作成されます。
シンボルの色は目的関数の値に対応します。
$ python3 plot_result_2dmap.py
作成された図を見ると、 T を小さくするごとに f(x) の最小値を与える点の付近にサンプルが集中していることがわかります。
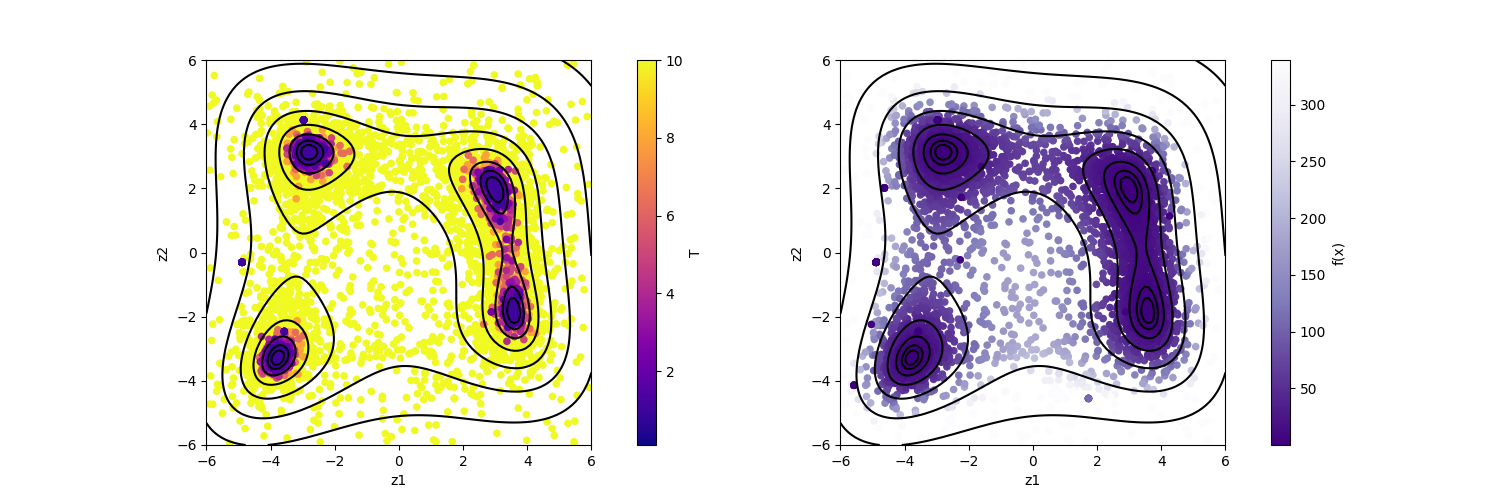
サンプルされたパラメータ。横軸は x1 , 縦軸は x2 を、色は T (左図), f(x) (右図)を表す。¶