ランダム探索¶
ここでは、ランダム探索を行い Himmelblau関数の最小化問題を解析する方法について説明します。
高次元問題など、グリッドサーチなどの他の手法が困難なときに有効な手法です。
ランダム探索はMPI並列化に対応しています。具体的な計算手順は minsearch の場合と同様です。
サンプルファイルの場所¶
サンプルファイルは sample/analytical/random_search にあります。
フォルダには以下のファイルが格納されています。
input.tomlメインプログラムの入力ファイル
plot_colormap_2d.py計算結果を可視化するためのプログラム
do.sh本チュートリアルを一括計算するために準備されたスクリプト
入力ファイルの説明¶
メインプログラム用の入力ファイル input.toml について説明します。記述方法の詳細については「入力ファイル」の項を参照してください。
[base]
dimension = 2
output_dir = "output"
[solver]
name = "analytical"
function_name = "himmelblau"
[runner]
[runner.log]
interval = 20
[algorithm]
name = "random_search"
seed = 12345
[algorithm.param]
max_list = [6.0, 6.0]
min_list = [-6.0, -6.0]
num_points = 100
[base], [solver], [runner] のセクションについては Nelder-Mead法による探索(minsearch)の場合と同じです。
[algorithm] セクションでは、使用するアルゴリスムとその設定を行います。
nameは使用するアルゴリズムの名前です。このチュートリアルでは、ランダム探索による解析を行うので、random_searchを指定します。seedはパラメータ生成に用いる疑似乱数のシードを指定します。
[algorithm.param] セクションで探索するパラメータのグリッドを指定します。
min_listとmax_listはそれぞれ探索範囲の最小値と最大値を指定します。num_pointsはランダムに生成するパラメータの個数を指定します。
この例では、\(-6.0 \leq x_1 \leq 6.0\), \(-6.0 \leq x_2 \leq 6.0\) の範囲でランダムに100点のパラメータ \((x_1, x_2)\) を生成して関数値を評価します。
計算の実行¶
最初にサンプルファイルが置いてあるフォルダへ移動します。(以下、ODAT-SEパッケージをダウンロードしたディレクトリの直下にいることを仮定します。)
$ cd sample/analytical/random_search
メインプログラムを実行します。計算時間は通常のPCで数秒程度で終わります。
$ mpiexec -np 4 python3 ../../../src/odatse_main.py input.toml | tee log.txt
ここではプロセス数4のMPI並列を用いた計算を行っています。
実行すると output ディレクトリとその下に各ランクのフォルダが作成され、ランクごとの計算結果が出力されます。
同時に、以下の様な出力が標準出力に書き出されます。
Make ColorMap
Iteration : 1/100
Iteration : 2/100
Iteration : 3/100
Iteration : 4/100
Iteration : 5/100
Iteration : 6/100
Iteration : 7/100
...
x1, x2 にランダムに生成したパラメータと、その時の関数値が出力されます。
最終的にランダムに生成した全ての点で計算された関数値が output/ColorMap.txt に出力されます。
今回の場合は、
5.155393 -2.203493 187.944291
-3.792974 -3.545277 3.179381
0.812700 1.146536 108.254643
5.574174 1.838125 483.841834
2.986880 1.842838 0.436331
2.972578 5.535681 719.799258
-5.899340 -4.722667 452.469102
-2.415555 1.876934 45.535582
3.717751 4.466111 330.797237
5.575771 2.684224 552.047948
...
のような結果が得られ、
1列目、2列目に x1, x2 の値、3列目に関数値が記載されます。
計算結果の可視化¶
ColorMap.txt を図示することで、関数の値が小さいパラメータがどこにあるかを推定することができます。そのような 2次元パラメータ空間のプロットを作成するプログラムが plot_colormap_2d.py に用意されています。
$ python3 plot_colormap_2d.py
上記を実行すると ColorMapFig.png が作成され、Himmelblau関数の関数値を表す等高線の上に、各点で評価した関数値がカラーマップとしてプロットされます。
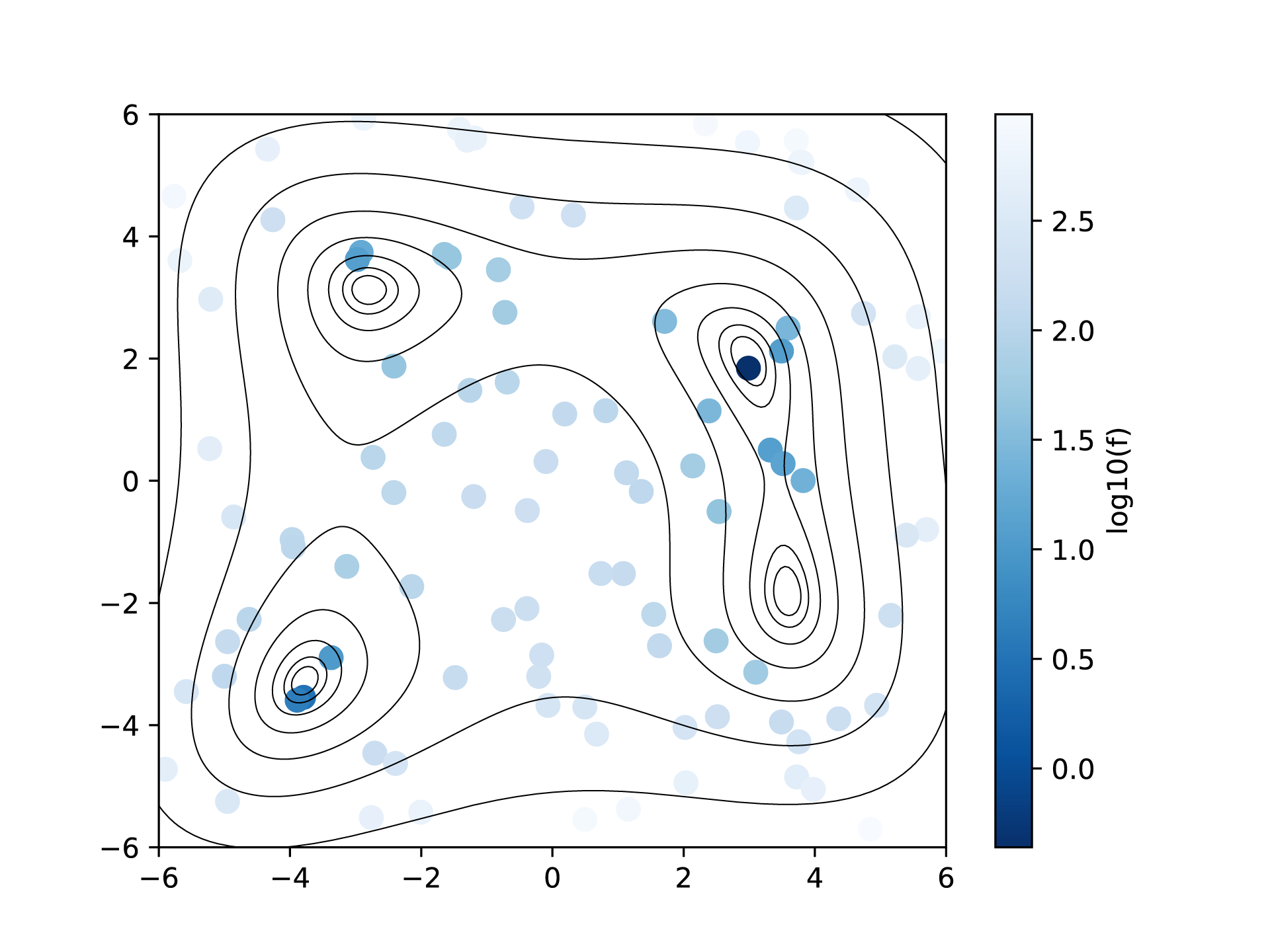
ランダム探索における2次元パラメータ空間上での関数値のカラーマップ。¶