PHYSBO の基本

はじめに

本チュートリアルでは例として、Cuの安定した界面構造の探索問題を扱います。 目的関数の評価にあたる構造緩和計算には、実際には1回あたり数時間といったオーダーの時間を要しますが、本チュートリアルでは既に評価済みの値を使用します。問題設定については、以下の文献を参照してください。

    1. Kiyohara, H. Oda, K. Tsuda and T. Mizoguchi, “Acceleration of stable interface structure searching using a kriging approach”, Jpn. J. Appl. Phys. 55, 045502 (2016).

それではサンプルデータを用いて、各手順を実際に行ってみましょう。

はじめに、PHYSBOをインポートします。

[1]:

import physbo

探索候補データの準備

まず、データを読み込みます。

[2]:

import numpy as np

def load_data():
    A =  np.asarray(np.loadtxt('data/s5-210.csv',skiprows=1, delimiter=',') )
    X = A[:,0:3]
    t  = -A[:,3]
    return X, t

[3]:

X, t = load_data()

以下、N: 探索候補の数 , d: 入力パラメータの次元数 とします。

X は N x d 次元の行列で、各行は探索候補である各パラメータセット (d 次元のベクトル) を表します。
t は N 次元のベクトルで、各探索候補の負のエネルギー(最適化したい目的関数の値) と対応します。 ※ 通常、ベイズ最適化を行う際は、Xのみを与え、tは存在しない状況からスタートします。そのため、実際に利用する際には、tの値はベイズ最適化の候補提案を受け、simulatorで評価することではじめて値が得られます。ここではチュートリアルのためにtをあらかじめ与えています。

PHYSBO では最適化の方向は「最大化」だと仮定します。

そのため、元々の問題設定は「エネルギー最小化」ですが、PHYSBOで最適化を行うにあたって、目的関数値にマイナスを掛けて「負のエネルギーの最大化」問題として扱っています。

[4]:

X

[4]:

array([[0. , 1. , 0. ],
       [0. , 1. , 0.1],
       [0. , 1. , 0.2],
       ...,
       [8. , 1.5, 3.4],
       [8. , 1.5, 3.5],
       [8. , 1.5, 3.6]])

[5]:

t

[5]:

array([-1.01301176, -1.01487066, -1.02044168, ..., -1.11680203,
       -2.48876352, -2.4971452 ])

探索パラメータのスケールを合わせるため、X の各列についてそれぞれ、平均が0, 分散が 1 となるように標準化します。

[6]:

X = physbo.misc.centering( X )

[7]:

X

[7]:

array([[-1.71079785, -1.46385011, -1.68585446],
       [-1.71079785, -1.46385011, -1.59219588],
       [-1.71079785, -1.46385011, -1.4985373 ],
       ...,
       [ 1.71079785,  1.46385011,  1.4985373 ],
       [ 1.71079785,  1.46385011,  1.59219588],
       [ 1.71079785,  1.46385011,  1.68585446]])

simulator の定義

PHYSBO に与える simulator クラスを定義します。
__call__ メソッドの返り値が、action を与えたときの目的関数値となります。
action は探索候補の ID (0, 1, …, N-1) を表します。
本チュートリアルでは、action が与えられたときに、既に計算された t の値をそのまま返すだけの simulator を定義しています。
他の問題に適用する際は、simulator クラスをカスタマイズしてください。
[8]:

class simulator:
    def __init__( self ):
        _, self.t = load_data()

    def __call__( self, action ):
        return self.t[action]

最適化の実行

policy のセット

まず、最適化の policy をセットします。

test_X に探索候補の行列 (numpy.array) を指定します。

[9]:

# policy のセット
policy = physbo.search.discrete.policy(test_X=X)

# シード値のセット
policy.set_seed(0)

policy をセットした段階では、まだ最適化は行われません。 policy に対して以下のメソッドを実行することで、最適化を行います。

  • random_search

  • bayes_search

これらのメソッドに先ほど定義した simulator と探索ステップ数を指定すると、探索ステップ数だけ以下のループが回ります。

  1. パラメータ候補の中から次に実行するパラメータを選択

  2. 選択されたパラメータで simulator を実行

  3. で返されるパラメータはデフォルトでは1つですが、1ステップで複数のパラメータを返すことも可能です。 詳しくは「複数候補を一度に探索する」の項目を参照してください。

また、上記のループを PHYSBO の中で回すのではなく、i) と ii) を別個に外部から制御することも可能です。つまり、PHYSBO から次に実行するパラメータを提案し、その目的関数値をPHYBOの外部で何らかの形で評価し（例えば、数値計算ではなく、実験による評価など）、それをPHYSBOの外部で何らかの形で提案し、評価値をPHYSBOに登録する、という手順が可能です。詳しくは、チュートリアルの「インタラクティブに実行する」の項目を参照してください。

ランダムサーチ

まず初めに、ランダムサーチを行ってみましょう。

ベイズ最適化の実行には、目的関数値が2つ以上求まっている必要があるため（初期に必要なデータ数は、最適化したい問題、パラメータの次元dに依存して変わります）、まずランダムサーチを実行します。

引数

  • max_num_probes: 探索ステップ数

  • simulator: 目的関数のシミュレータ (simulator クラスのオブジェクト)

[10]:

res = policy.random_search(max_num_probes=20, simulator=simulator())

実行すると、各ステップの目的関数値とその action ID、現在までのベスト値とその action ID が以下のように出力されます。

0020-th step: f(x) = -1.048733 (action=1022)
   current best f(x) = -0.963795 (best action=5734)

ベイズ最適化

続いて、ベイズ最適化を以下のように実行します。

引数

  • max_num_probes: 探索ステップ数

  • simulator: 目的関数のシミュレータ (simulator クラスのオブジェクト)

  • score: 獲得関数(acquisition function) のタイプ。以下のいずれかを指定します。

    • TS (Thompson Sampling)

    • EI (Expected Improvement)

    • PI (Probability of Improvement)

  • interval: 指定したインターバルごとに、ハイパーパラメータを学習します。 負の値を指定すると、ハイパーパラメータの学習は行われません。 0 を指定すると、ハイパーパラメータの学習は最初のステップでのみ行われます。

  • num_rand_basis: 基底関数の数。0を指定すると、Bayesian linear modelを利用しない通常のガウス過程が使用されます。

[11]:

res = policy.bayes_search(max_num_probes=80, simulator=simulator(), score='TS',
                                                  interval=20, num_rand_basis=5000)

結果の確認

探索結果 res は history クラスのオブジェクト (physbo.search.discrete.results.history) として返されます。
以下より探索結果を参照します。

  • res.fx : simulator (目的関数) の評価値の履歴。

  • res.chosen_actions: simulator を評価したときの action ID (パラメータ) の履歴。

  • fbest, best_action= res.export_all_sequence_best_fx(): simulator を評価した全タイミングにおけるベスト値とその action ID (パラメータ)の履歴。

  • res.total_num_search: simulator のトータル評価数。

各ステップでの目的関数値と、ベスト値の推移をプロットしてみましょう。
res.fx, best_fx はそれぞれ res.total_num_search までの範囲を指定します。
[12]:

import matplotlib.pyplot as plt
%matplotlib inline

[13]:

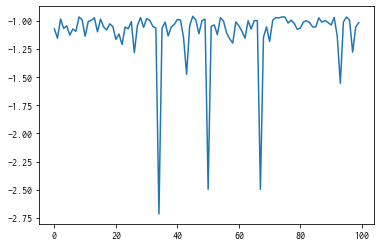
plt.plot(res.fx[0:res.total_num_search])

[13]:

[<matplotlib.lines.Line2D at 0x7fe0d9310580>]
../_images/notebook_tutorial_basic_22_1.png 
[14]:

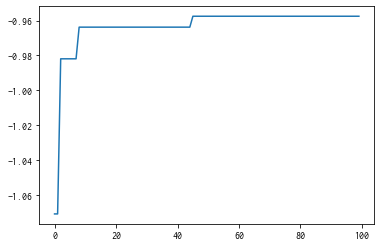
best_fx, best_action = res.export_all_sequence_best_fx()
plt.plot(best_fx)

[14]:

[<matplotlib.lines.Line2D at 0x7fe0d93eaaf0>]
../_images/notebook_tutorial_basic_23_1.png

結果のシリアライズ

探索結果は save メソッドにより外部ファイルに保存できます。

[15]:

res.save('search_result.npz')

[16]:

del res

保存した結果ファイルは以下のようにロードします。

[17]:

res = physbo.search.discrete.results.history()
res.load('search_result.npz')

[ ]: