6. アルゴリズム¶

6.1. テンソルネットワーク状態¶

テンソルネットワーク状態 (Tensor network states (TNS)) とは小さなテンソルの積、繋がりで表現された変分波動関数です [TNS] 。例えば、\(N\) 個の \(S=1/2\) 量子スピン系では、その波動関数は直積状態の基底を用いて、

\[|\Psi\rangle = \sum_{s_i = \uparrow,\downarrow} \Psi_{s_1,s_2,\dots,s_N} |s_1,s_2,\dots,s_N\rangle\]

と表せます。テンソルネットワーク状態では、この展開係数 \(\Psi_{s_1,s_2,\dots,s_N}\) はテンソルのネットワークで表現され、例えば

\[\Psi_{s_1,s_2,\dots,s_N} = \mathrm{tTr}\left[T^{(1)}[s_1]T^{(2)}[s_2]\cdots T^{(N)}[s_N]\right],\]

と書くことができます。ここで、 \(\mathrm{tTr}[\dots]\) はテンソルネットワークの縮約を表し、 \(T^{(i)}[s_i]\) はテンソルを表しています。行列積状態 (matrix product state (MPS)) と呼ばれるテンソルネットワーク状態の場合 [MPS] , \(T^{(i)}[s_i]\) は \(s_i\) が与えられると行列になっていて、 \(\mathrm{tTr}[\dots]\) はこの場合、通常の行列積になります：

\[\Psi_{s_1,s_2,\dots,s_N}^{\mathrm{MPS}} = T^{(1)}[s_1]T^{(2)}[s_2]\cdots T^{(N)}[s_N],\]

ここで、 \(T^{(1)}[s_1]\) 、 \(T^{(i)}[s_i] (i\neq 1, N)\) 、 \(T^{(N)}[s_N]\) の形状はそれぞれ、 \(1 \times D_1\) 、 \(D_{i-1} \times D_{i}\) 、 \(D_{N-1} \times 1\) であると仮定しました。

このようなTNSを基底状態波動関数の近似に用いる場合、その精度は \(D_i\) によって制限されます。 \(D_i\) は ボンド次元 と呼ばれています。テンソルネットワークのダイアグラム表記を用いると、 MPSは

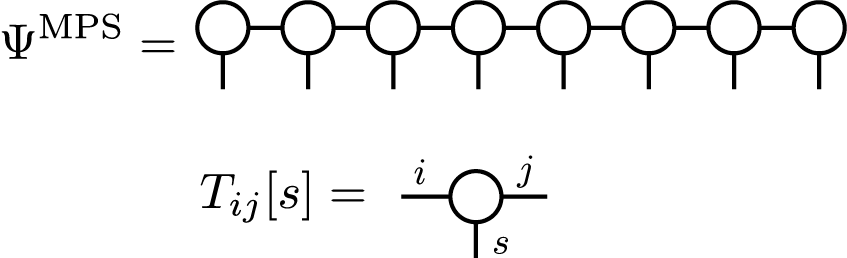
のように描くことができます。このMPSは有限系の波動関数を表していますが、同様にして、無限系の波動関数を表わす、無限に長いMPSを考えることもできます。特に、波動関数が格子の（ある長さの）並進に対して対称性を持っている場合、少数の独立なテンソルを繰り返すことで、無限系のMPS (infinite MPS (iMPS)) を作ることができます。２サイトの並進対称性の場合、このような iMPS は

と表せます。ここで、同じ色のテンソルは、同じ要素を持つテンソルです。

TeNeS では、2次元の無限に広がったテンソル積状態 (infinite tensor product states (iTNS)) を取り扱います。この iTPS は iMPS の高次元への自然な拡張になっています。 TeNeSでは、並進対称性をもった正方格子テンソルネットワークを仮定しており、ダイヤグラムでは、

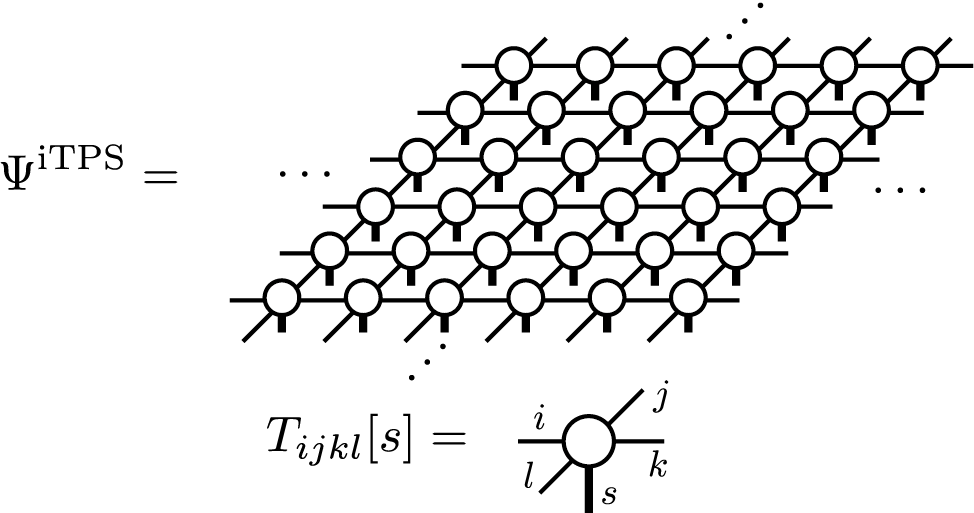
のように描けます。TeNeSではこのiTPSを用いて、2次元量子多体系の基底状態を近似的に計算します。なお、正方格子テンソルネットワークは、正方格子模型だけでなく、適切なマッピングにより、ハニカム格子模型、三角格子模型など様々な2次元格子模型に適用できます。

6.2. iTPS の縮約¶

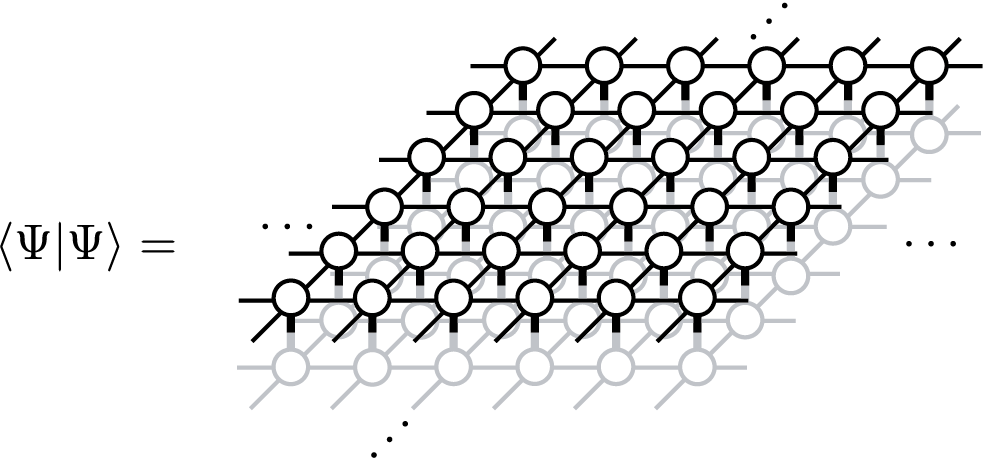
で与えられます。この形のテンソルネットワークは、しばしば、ダブルレイヤー（double layered）テンソルネットワークと呼ばれます。ダブルレイヤーテンソルネットワークの縮約計算は、通常、非常に大きな計算コストが必要です。MPS（や iMPS）の場合には、幸いにも、局所的なテンソルで構成される転送行列を考えることなどによって、効率的に計算することができます。しかし、TPS（や iTPS）の場合、厳密な縮約計算は小さいクラスター（又は小さい半径の無限シリンダー）を除いてほぼ不可能で、通常、近似的な縮約計算法を用います。TeNeSでは、角転送行列繰り込み群法（corner transfer matrix renormalization group (CTMRG) [CTMRG] と呼ばれる、無限に広がったダブルレイヤーテンソルネットワークを 角転送行列 と エッジテンソル を用いて近似する方法を採用しています。

ダブルレイヤーテンソルネットワークを局所的に縮約したテンソル

を使って単純化すると、角転送行列表現に対応するテンソルネットワークダイアグラムは、

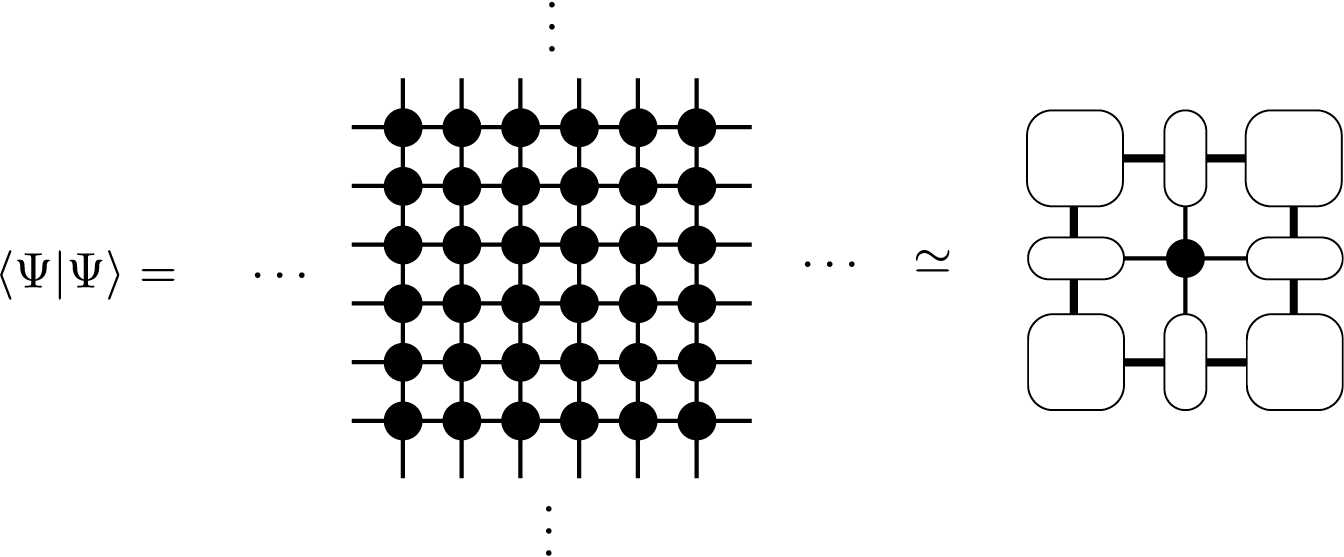
と表されます。角転送行列とエッジテンソルは、

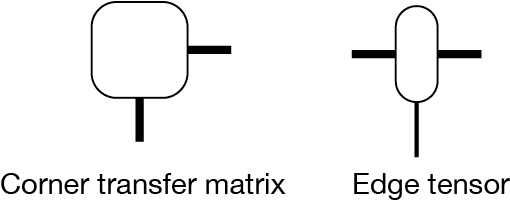
のように定義されています。角転送行列表現の精度は、ダイアグラム中で太線で表現した、角転送行列のボンド次元 \(\chi\) によって制限されます。

CTMRGのアルゴリズムでは、角転送行列とエッジテンソルに局所的なテンソルを吸収していくことでそれらをアップデートし、結果が収束するまで繰り返します。例えば、 left move と呼ばれる吸収手続きは、ダイアグラムでは

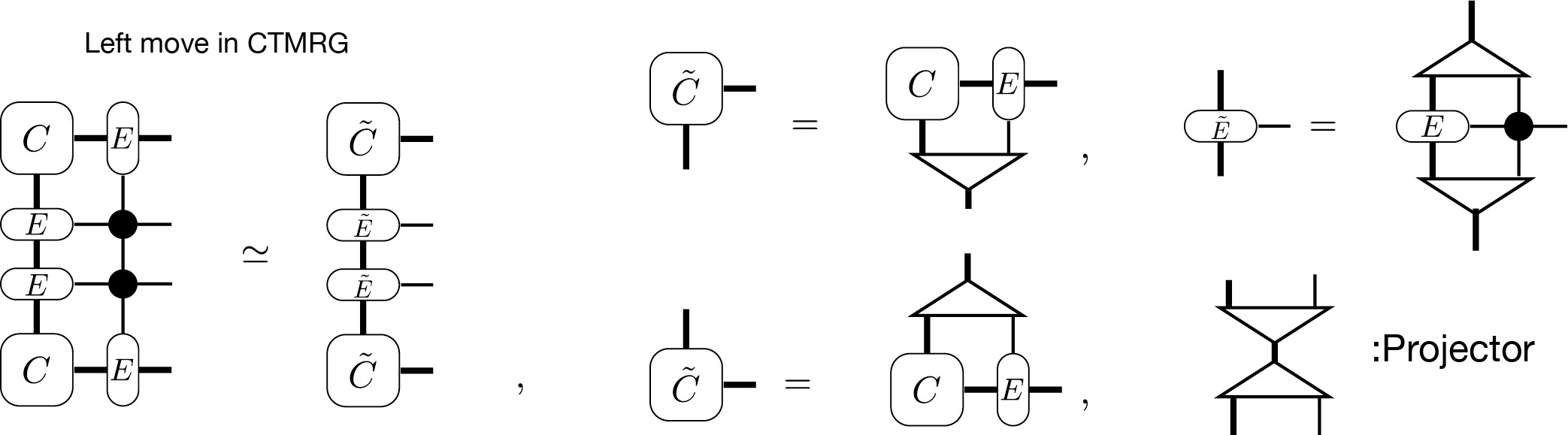
と表されます。このダイアグラムに現れる プロジェクター は、いくつかの方法で計算することができ [CTMRG] 、自由度を \(\chi\) に減らす働きをします。

ボンド次元 \(D\) のiTPSを用いて、ボンド次元 \(\chi\) の角転送行列表現を考える場合、CTMRGの計算コストは、 \(O(\chi^2 D^6)\) と \(O(\chi^3 D^4)\) の大きな方でスケールします。ここで、ダブルレイヤーテンソルネットワークのボンド次元は、局所縮約したテンソルを用いる表現では、 \(D^2\) になっていることに注意してください。このため、通常、 \(\chi\) は \(\chi \propto O(D^2)\) のように \(D^2\) に比例して増やします。この条件では、CTMRGの計算コストは \(O(D^{10})\) になり、メモリ量は \(O(D^{8})\) になります。なお、ここで述べた計算コストを得るためには、疎行列の特異値分解（SVD）を用いる必要があります、代わりに、密行列のSVDを用いる場合、計算コストは \(O(D^{12})\) となります。

いったん収束した角転送行列とエッジテンソルを得れば、 \(\langle \Psi|O|\Psi\rangle\) も効率的に計算することができます。例えば、局所磁化 \(\langle \Psi|S^z_i|\Psi\rangle\) は、

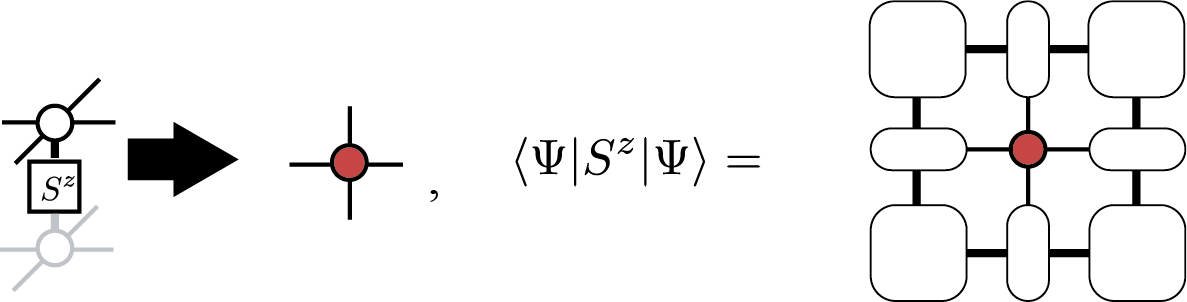
のように表わされ、同様に最近接相関 \(\langle \Psi|S^z_iS^z_{i+1}|\Psi\rangle\) は

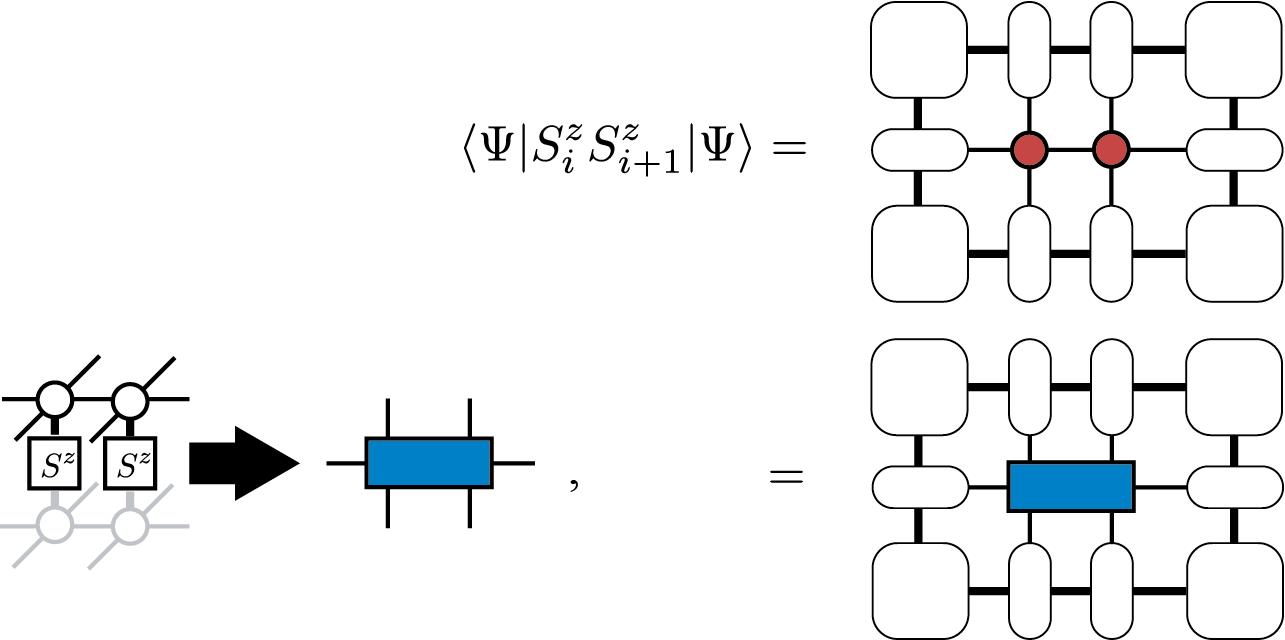
と表現することができます。また、ダイアグラムの２番目の表記を用いることで、任意の２サイト演算子の期待値も計算できることがわかります。このようなダイグラムを任意の演算子に対して描くことは可能ですが、クラスターが大きくなるとその縮約計算に必要となる計算コストが莫大になることに注意してください。

6.3. iTPSの最適化¶

iTPSを基底状態の変分波動関数として用いる場合、iTPSが最小のエネルギー期待値

\[E = \frac{\langle \Psi|\mathcal{H}|\Psi\rangle}{\langle \Psi|\Psi\rangle},\]

を与えるように、テンソルを最適化する必要があります。ここで、 \(\mathcal{H}\) は対象系のハミルトニアンを表しています。 TeNeSでは、虚時間発展（the imaginary evolution (ITE)）法と変分最適化（the variational optimization）法という二つの手法のうち、前者の ITE を採用しています。TeNeS では、iTPSの範囲での近似的な虚時間発展

\[|\Psi^{\mathrm{iTPS}} \rangle \simeq e^{-T \mathcal{H}} |\Psi_0\rangle,\]

を考えます。ここで、 \(|\Psi_0 \rangle\) は任意の初期 iTPS です。もし、 \(T\) が十分に大きければ、左辺の \(|\Psi^{\mathrm{iTPS}}\rangle\) は基底状態の良い近似になっていると考えることができます。

TeNeSでは、ハミルトニアンは短距離の二体相互作用の和で

\[\mathcal{H} = \sum_{\{(i,j)\}}H_{ij},\]

のように表されていると仮定し、小さな時間刻み \(\tau\) の虚時間発展演算子に対してSuzuki-Trotter 分解

\[e^{-\tau \mathcal{H}} = \prod_{\{(i,j)\}} e^{-\tau H_{ij}} + O(\tau^2).\]

を適用します。ここでは、一次の近似を考えましたが、より高次の分解を考えることもできます。Suzuki-Trotter 分解の形を用いることで、虚時間発展は

\[e^{-T \mathcal{H}} |\Psi_0\rangle = \left( \prod_{\{(i,j)\}} e^{-\tau H_{ij}}\right)^{N_{\tau}} |\Psi_0\rangle + O(\tau),\]

のように書き下すことができます。ここで、 \(N_{\tau} = T/\tau\) は十分に小さな \(\tau\) での虚時間発展のステップ数です。この式の右辺を計算するために、 \(\prod_{\{(i,j)\}}\) の積をいくつかの部分集合に分解します。それぞれの部分集合内では, （局所的な）虚時間発展演算子はお互いに交換し、考えているiTPSと同じ並進対称性を持っているとします。例えば、２サイトの iMPS で、１元系の最近接相互作用ハミルトニアンを考えた場合、二つの部分集合を用いて、

のように虚時間発展を分解することができます。

次に、それぞれの虚時間発展演算子の部分集合を適用した波動関数を、ボンド次元 \(D\): の新しいiTPSとして

\[|\Psi_{\tau}^{\mathrm{iTPS}} \rangle \simeq \prod_{\{(i,j) \in \mathrm{subset}_n \}}e^{-\tau H_{ij}} |\Psi^{\mathrm{iTPS}}\rangle,\]

のように近似します。ここで \(\prod_{\{(i,j) \in \mathrm{subset}_n \}}\) は \(n\) 番目の部分集合内の演算子の積を表し、 \(|\Psi_{\tau}^{\mathrm{iTPS}}\rangle\) は新しい iTPS です。ダイアグラムを用いるとこの式は、

のように表現できます。一般に、 \(e^{-\tau H_{ij}}\) をかけることで厳密な iTPS 表現のボンド次元は増大してしまうことに注意してください。したがって、虚時間発展のシミュレーションを安定して継続するためには、ボンド次元をある一定値 \(D\) まで毎回打ち切る（ truncate ）必要があります。

素朴には、効率的な打ち切りは、最小化問題

\[\min \left \Vert |\Psi_{\tau}^{\mathrm{iTPS}} \rangle -\prod_{\{(i,j) \in \mathrm{subset}_n \}} e^{-\tau H_{ij}} |\Psi^{\mathrm{iTPS}}\rangle \right \Vert^2\]

を解くことで行えます。しかし、この最小化問題を解く計算コストは、主にiTPSの並進対称性で問題が非線形問題になっているために、非常に膨大になってしまいます。そこで、通常は、代わりの問題として、局所的な一つの虚時間発展演算子だけを適用して、それを近似する iTPS \(|\Psi_{\tau}^{\mathrm{iTPS}}\rangle\) を探す問題を考えます。ここで、新しいiTPSでは、元の \(|\Psi^{\mathrm{iTPS}}\rangle\) と比較して、数個のテンソルだけが変更されています。この局所的な最小化問題は

\[\min \left \Vert |\Psi_{\tau}^{\mathrm{iTPS}} \rangle - e^{-\tau H_{ij}} |\Psi^{\mathrm{iTPS}}\rangle \right \Vert^2\]

と書くことができます。一次元の最近接相互作用の場合、この最小化問題に対応するダイアグラムは、

で与えられます。

差の二乗ノルム \(\left \Vert |\Psi_{\tau}^{\mathrm{iTPS}} \rangle - e^{-\tau H_{ij}} |\Psi^{\mathrm{iTPS}}\rangle \right \Vert^2\) は、例えば CTMRG 等を使うことで効率的に計算できるため、この最適化問題は簡単に解くことができます [ITE] 。ここで新しく得られる iTPS は並進対称性を破っていますが、アップデートされたテンソルを他の場所に コピー することで、並進対称な iTPS を作ることができます。

このiTPSは元の最小化問題の近似解だと考えることができます。このような虚時間発展の方法は、 full update 法と呼ばれます。 full update 法の計算の大部分は CTMRG であり、SVDの方法に応じて、計算コストは \(O(D^{10})\) または \(O(D^{12})\) でスケールします。

Simple update 法は虚時間発展を用いた、より計算コストの小さい最適化手法です。Simple update法では、CTMRGによる重い計算を避けるために, 波動関数全体ではなく、局所的なテンソルネットワークを考えます [SimpleUpdate] 。例えば最近接相互作用の場合には、以下のような局所的な最適化問題を考えます。

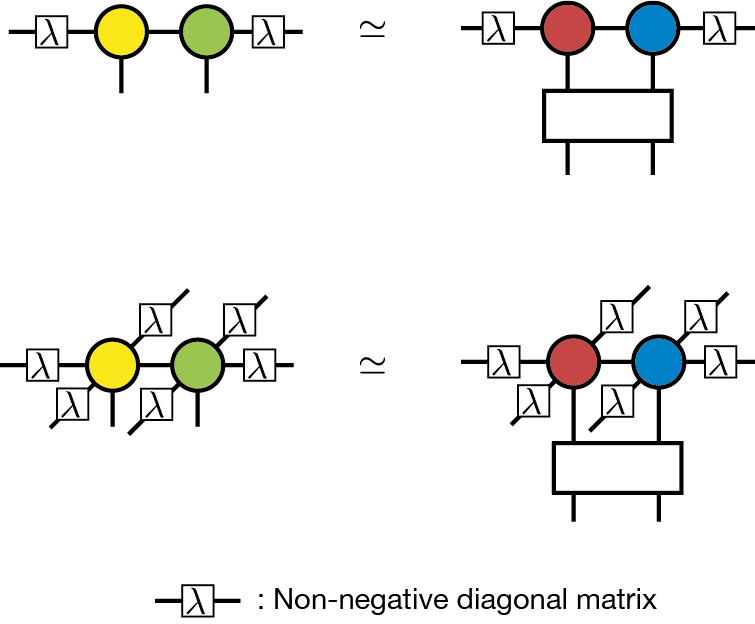
このダイアグラムでは、 \(\lambda_i\) は非負の対角行列を表していて、これはボンド \(i\) の先にある無視した環境を表わす平均場だと考えることができます。 \(\lambda_i\) の具体的な定義は後で与えられます。このダイアグラムが表わす最適化問題は、テンソル二つと虚時間発展演算子一つが一体となった行列の低ランク近似と見做すことができるため、SVDを用いて解くことができます。この手続きは、ダイアグラムを用いて、

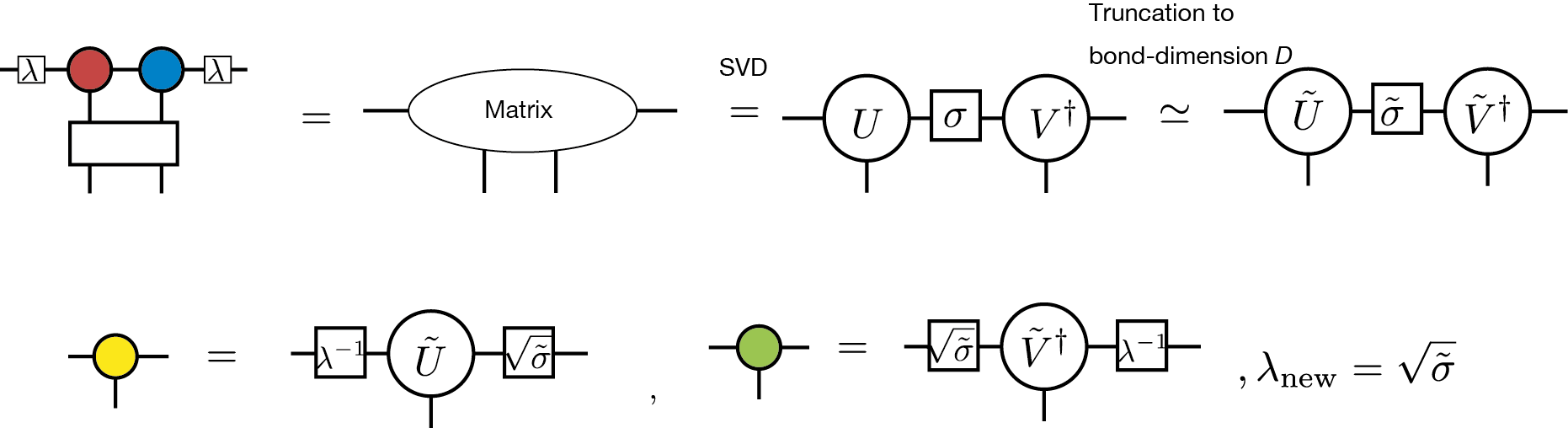
と表すことができます。計算途中のSVDで出てきた行列の特異値は、次のステップでの平均場 \(\lambda\) として利用されます。Simple update法の計算コストは、行列を構成する前にQR分解を行うことで、 \(O(D^{5})\) になります [QR] 。したがって、simple update法はfull update法よりもずっと計算コストが軽くなっています。

ただし、simple update法はfull update法よりも計算コストが小さいですが、simple update法は初期状態依存性が強く、また、最終結果の局所磁化の大きさを過剰評価する問題が知られています。したがって、未知の問題に適用する場合には、得られた結果を慎重に検証する必要があります。

6.4. iTPSを用いた実時間発展¶

基底状態を計算する際に用いた虚時間発展のアルゴリズム、simple update法やfull update法を用いて、量子状態の実時間発展を計算することもできます。TeNeSでは、虚時間発展の場合と同様に、時刻 \(t\) における量子状態

\[|\Psi(t)\rangle = e^{-it\mathcal{H}} |\Psi_0\rangle,\]

をiTPSで近似することで、近似的な時間発展を計算できます。虚時間発展と実時間発展の違いは、指数関数の肩にあるハミルトニアン \(\mathcal{H}\) の係数が \(-\tau\) か \(-it\) かだけの違いですので、実時間発展でも、Suzuki-Trotter分解を適用することで、虚時間発展で用いたのと全く同じsimple update法とfull update法を用いて、近似的な時間発展を計算できます。

iTPS（および、その他のテンソルネットワーク状態）を用いた実時間発展は、基底状態の計算に虚時間発展を用いる場合と、以下の二つの点で大きく異なっています。

一つの大きな違いは、対象となる量子状態の量子エンタングルメントの大きさです。虚時間発展では、時間発展が進むにつれて基底状態に向かうため、計算の過程で、量子状態の量子エンタングルメントが極端に大きくなることはなく、iTPSでの記述が破綻する可能性が低いですが、実時間発展では、典型的には（初期状態のiTPSがハミルトニアンの固有状態である場合を除いて）、時間発展とともに量子エンタングルメントが増大します。そのため、iTPSでの近似精度を保つにには、長時間になればなるほど、iTPSのボンド次元を大きくしなくてはなりません。もちろん、ボンド次元を大きくするとその分計算コストが増大しますので、現実的な計算資源の範囲では、iTPSを用いて実時間発展を精度よく近似できるのは、短時間に限定されます。適用可能な時間範囲はモデルに依存しますが、例えばスピン模型では、相互作用の典型的な大きさ \(J\) に対して、 \(t = O(1/J)\) 程度の時間が限界になることが多いです。

もう一つの違いは、再現したい物理現象の特徴です。虚時間発展を基底状態の計算に用いる場合には、十分に長い虚時間発展を行った後に、最終的に基底状態に到達できていれば良いので、途中の量子状態が、正しい虚時間発展の経路から多少ずれていても、大きな問題は生じません。一方で、実時間発展を行う場合には、最終状態だけでなく、量子状態の時間発展そのものに興味があることが多いと思われます。時間発展の経路を精度よく近似するためには、iTPSのボンド次元を大きくするだけでなく、Suzuki-Trotter分解での時間刻み \(\delta t\) も十分に小さくする必要があります。また、状況に応じて、高次のSuzuki-Trotter分解を用いた方が効率的な場合もあります。TeNeSでは、最終的にtenesに入力する入力ファイルの evolution セクションを編集することで、高次のSuzuki-Trotter分解に対応することができます。

6.5. 有限温度状態の表現¶

ここまでは、量子多体系の純粋状態 \(|\Psi\rangle\) を対象としたテンソルネットワーク表現を考えていましたが、同様の考えで、有限温度に対応する混合状態

\[\rho(\beta) = \frac{e^{-\beta \mathcal{H}}}{\mathrm{Tr} e^{-\beta \mathcal{H}}}\]

のテンソルネットワーク表現を考えることもできます。ここで、 \(\beta\) は温度 \(T\) に対応する逆温度 \(\beta = 1/T\) を表しています。

純粋状態の時と同様に、 \(N\) 個の \(S=1/2\) 量子スピン系を例に考えると、有限温度の混合状態は

\[\rho(\beta) = \sum_{s_i=\uparrow, \downarrow, s_i' =\uparrow, \downarrow} \left(\rho(\beta)\right)_{s_1,s_2,\dots, s_N}^{s_1', s_2', \dots, s_N'} |s_1', s_2', \dots, s_N'\rangle \langle s_1, s_2, \dots, s_N|\]

と表すことができます。この展開係数 \(\left(\rho(\beta)\right)_{s_1,s_2,\dots, s_N}^{s_1', s_2', \dots, s_N'}\) のテンソルネットワークによる表現は、例えば、MPSを行列（演算子）に一般化した、行列積演算子（Matrix Product Operator(MPO)）を用いて、

\[\left(\rho^{\mathrm{MPO}}(\beta)\right)_{s_1,s_2,\dots, s_N}^{s_1', s_2', \dots, s_N'} = T^{(1)}[s_1, s_1']T^{(2)}[s_2, s_2']\cdots T^{(N)}[s_N, s_N']\]

で表すことができ、対応するダイアグラムは

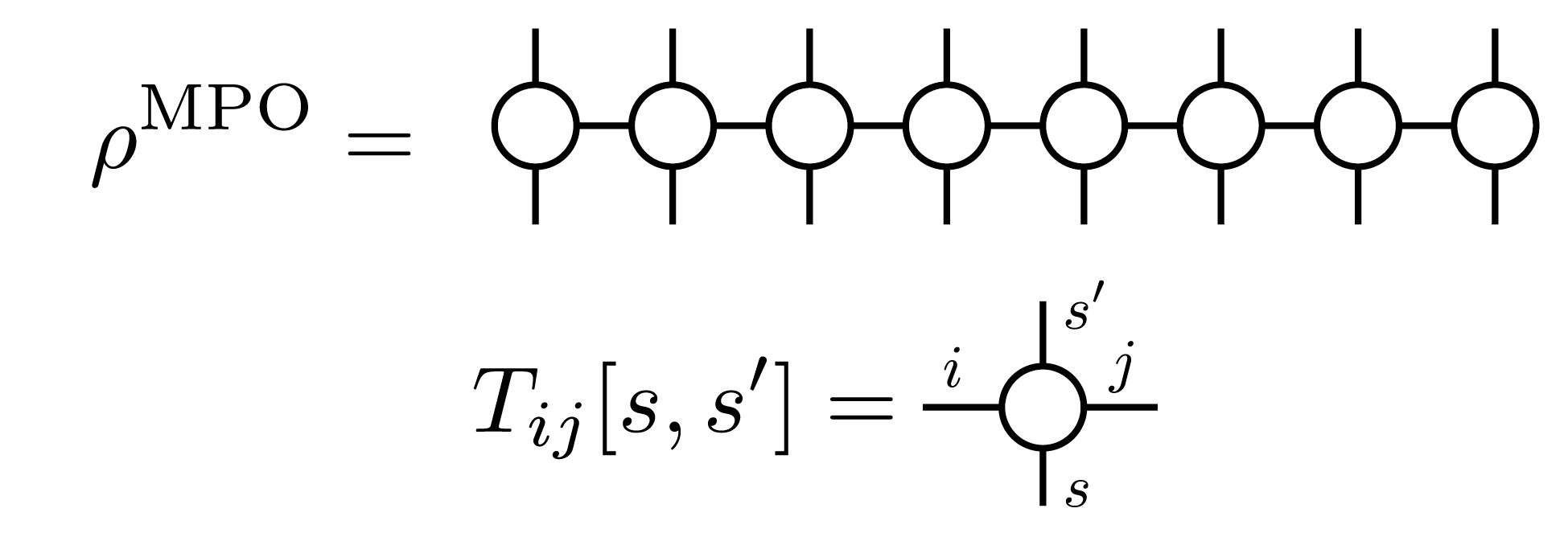
のように書くことができます。純粋状態の場合と同様に、並進対称性がある混合状態に対しては、同じテンソルを無限に繰り返すiMPOにより、無限系の状態を表すこともでき、例えば、1次元的な2サイトの並進対称性を持つ状態では、対応するiMPOのダイアグラムは

のようになります。

TeNeSでは、混合状態の表現として、二次元の無限に広がったテンソル積演算子 (infinite tensor product operator (iIPO))を取り扱い [TPO] 、特に、並進対称性を持った正方格子型のネットワークを仮定します。この場合、iTPOのダイアグラムは、

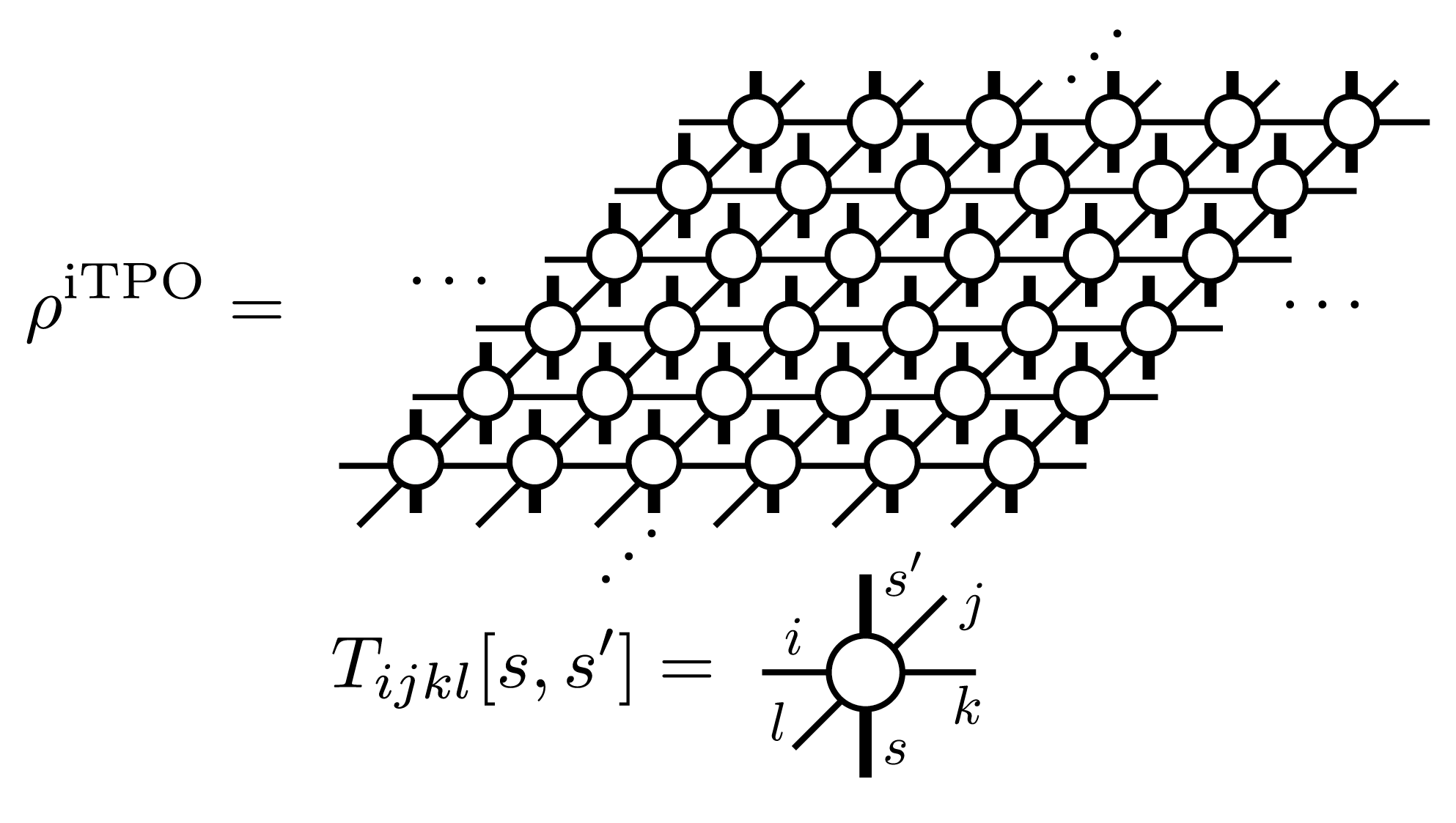
と書くことができます。

TeNeSでは、有限温度の混合状態 \(\rho(\beta)\) を、温度無限大に対応する \(\rho(\beta=0)\) を初期状態とした虚時間発展

\[\rho(\beta) = e^{-\frac{\beta}{2} \mathcal{H}} \rho(0) e^{-\frac{\beta}{2} \mathcal{H}/2}\]

を用いて計算します。ここで、温度無限大では、密度行列は単位行列になっていることに注意してください。この性質から、例えば、温度無限大の状態のiMPO表現は、局所的な単位行列のテンソル積になり、ダイアグラムでは、

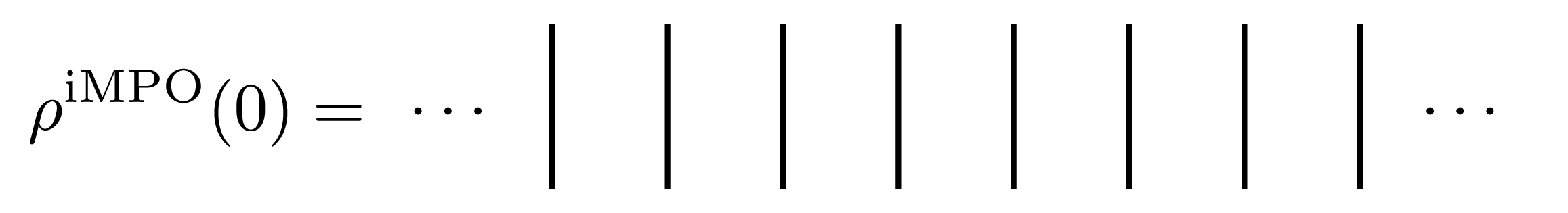
のように、単位行列に対応する"線"が並ぶことになります。

TeNeSでは、混合状態に対する虚時間発展を、純粋状態での虚時間発展の単純な拡張として、iTPOの範囲内での近似的な虚時間発展として計算します。混合状態の場合での計算には、純粋状態の場合に用いた虚時間発展演算子のSuzuki-Trotter分解やsimple update法, full update法をほぼ、そのままの形で適用することができます（TeNeSでは現時点で、simple update法のみをサポートしています）。

混合状態の場合に解く局所的な最小化問題は

\[\min \left \Vert \rho_{\tau}^{\mathrm{iTPO}} - e^{-\frac{\tau}{2} \mathcal{H}_{ij}/2} \rho^{\mathrm{iTPO}} e^{-\frac{\tau}{2} \mathcal{H}_{ij}}\right \Vert^2\]

の形で記述でき、対応するダイアグラムは、（見やすさを考えて、iMPOの形で描くと）

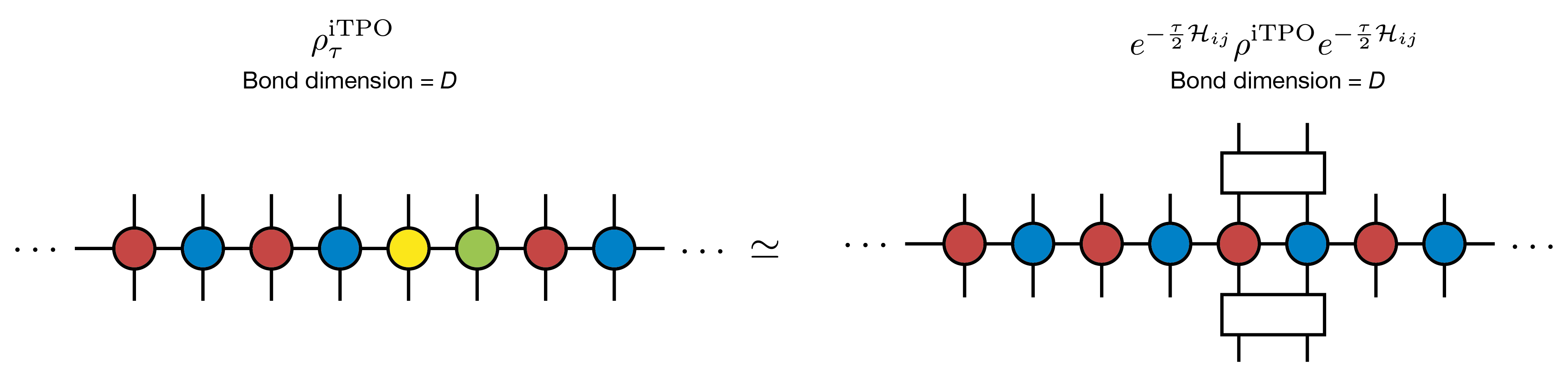
になります。

iTPOを用いた有限温度状態の計算と、iTPSを用いた純粋状態の計算における、アルゴリズム上の一番大きな違いは、期待値計算に現れるテンソルネットワークになります。混合状態 \(\rho\) が与えられた際の物理量 \(O\) の期待値は、

\[\langle O \rangle_\rho = \frac{\mathrm{Tr} (\rho O)}{\mathrm{Tr} \rho}\]

で計算されますが、 \(\mathrm{Tr}\) は、iTPOの対応する上下の足をつなぐことに相当するので、iTPOの局所的なの上下の足をつなげたテンソル

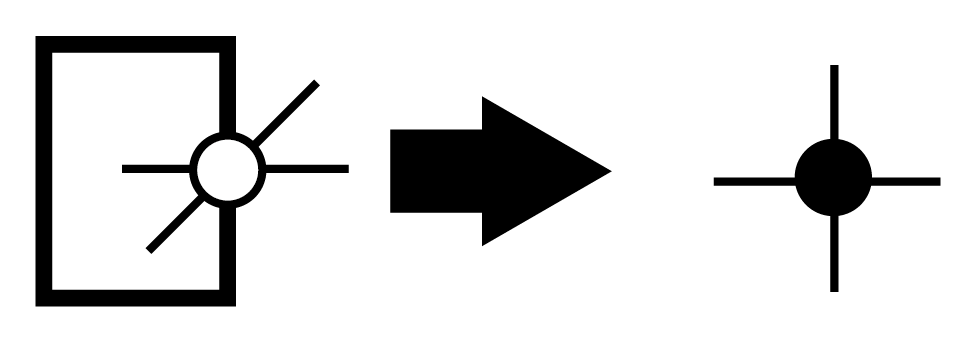
を用いると、例えば、分母の \(\mathrm{Tr} \rho\) は、純粋状態の期待値計算で現れた二次元正方格子のダイアグラムと同一の構造になり、角転送行列表現とCTMRGを用いた近似計算が可能になります。

ボンド次元 \(D\) のiTPOを用いて、ボンド次元 \(\chi\) 角転送行列表現を考える場合のCTMRG計算コストは、 \(O(\chi^2 D^4)\) と \(O(\chi^3 D^3)\) の大きな方でスケールします。この計算量は、同じボンド次元 \(D\) の純粋状態に対するCTMRGと比べて小さくなっていますが、違いの原因は、黒丸で示したテンソルのボンド次元が、純粋状態の計算では \(D^2\) になっている一方で、混合状態の場合には \(D\) のままであることです。この違いに対応して、角転送行列表現のボンド次元 \(\chi\) も、純粋状態とは異なり、 \(\chi \propto O(D)\) のように \(D\) に比例して増やせば良いことになります。この条件の下では、CTMRGの計算コストは \(O(D^6)\) になり、必要なメモリ量は \(O(D^4)\) になります。このように、同じ \(D\) iTPSと比べて、iTPOによる有限温度計算の計算コストは大幅に小さいため、有限温度計算では基底状態の計算よりも大きなボンド次元 \(D\) を用いた計算が可能です。

純粋状態の場合と同様に、一旦、収束した角転送行列とエッジテンソルを計算することができれば、\(\mathrm{Tr} (\rho O)\) も、純粋状態の場合と同様に効率的に計算できます。例えば、局所磁化 \(\mathrm{Tr} (\rho S_i^z)\) の場合は、演算子を含んだテンソルを

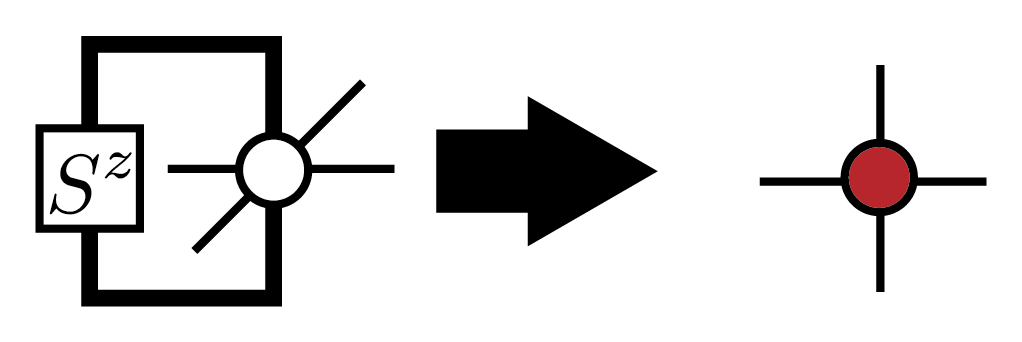
のように定義することで、純粋状態の \(\langle \Psi|S_i^z|\Psi\rangle\) と同じダイアグラムで計算することができます。

最後に、iTPOによる近似の欠点について触れておきます。混合状態の密度行列は、エルミートであり、また、その固有値は非負になっている、半正定値行列です。一方で、iTPOで密度行列を近似した場合、この半正定値性は保証されないため、iTPOで近似した密度行列から計算した物理量では、例えば、エネルギーが基底状態エネルギーよりも低くなったりするなどといった、非物理的な振る舞いが見られることがあります。これは、iTPO表現の問題であるため、期待値を計算する際のCTMRGの精度をボンド次元 \(\chi\) を増大することで改善しても回避することができません。物理的な振る舞いを回復するには、iTPOのボンド次元 \(D\) を増やして、密度行列の近似精度を上げる必要があります。

このような非物理的な振る舞いを避ける別の表現として、密度行列の純粋状態化（Purification）を用いて、純粋状態化された密度行列を、iTPOで表現する手法も提案されています [Purification] 。ただし、この場合には、期待値計算の際に現れるダイアグラムが、純粋状態の場合と同様にダブルレイヤー構造となるため、計算量が大きくなり、扱えるボンド次元 \(D\) が直接的なiTPO表現よりも小さくなってしまいます。

参考文献

[TNS] R. Orús, A practical introduction to tensor networks: Matrix product states and projected entangled pair states, Annals. of Physics 349, 117 (2014). link; R. Orús, Tensor networks for complex quantum systems, Nature Review Physics 1, 538 (2019). link; 西野友年、大久保毅 テンソルネットワーク形式の進展と応用, 日本物理学会誌 72, 702 (2017). link; 大久保毅 テンソルネットワークによる情報圧縮とフラストレート磁性体への応用, 物性研究・電子版 7, 072209 (2018) link.

[MPS] U. Schollwcök, The density-matrix renormalization group in the age of matrix product states, Annals. of Physics 326, 96 (2011). link

[CTMRG] T. Nishino and K. Okunishi, Corner Transfer Matrix Renormalization Group Method, J. Phys. Soc. Jpn. 65, 891 (1996).; R. Orús and G. Vidal, Simulation of two-dimensional quantum systems on an infinite lattice revisited: Corner transfer matrix for tensor contraction, Phys. Rev. B 80, 094403 (2009). link ; P. Corboz et al., Competing States in the t-J Model: Uniform d-Wave State versus Stripe State, Phys. Rev. Lett. 113, 046402 (2014). link

[ITE] J. Jordan et al., Classical Simulation of Infinite-Size Quantum Lattice Systems in Two Spatial Dimensions, Phys. Rev. Lett. 101, 250602, (2008). link; R. Orús and G. Vidal, Simulation of two-dimensional quantum systems on an infinite lattice revisited: Corner transfer matrix for tensor contraction, Phys. Rev. B 80, 094403 (2009). link

[SimpleUpdate] H. G. Jiang et al., Accurate Determination of Tensor Network State of Quantum Lattice Models in Two Dimensions, Phys. Rev. Lett. 101, 090603 (2008). link

[QR] L. Wang et al., Monte Carlo simulation with tensor network states, Phys. Rev. B 83, 134421 (2011). link

[TPO] A. Kshetrimayum, M. Rizzi, J. Eisert, and R. Orús, Tensor Network Annealing Algorithm for Two-Dimensional Thermal States, Phys. Rev. Lett. 122, 070502 (2019). link

[Purification] P. Czarnik, J. Dziarmaga, and P. Corboz, Time evolution of an infinite projected entangled pair state: An efficient algorithm, Phys. Rev. B 99, 035115 (2019). link; P. Czarnik and J. Dziarmaga, Time evolution of an infinite projected entangled pair state: An algorithm from first principles, Phys. Rev. B 98, 045110 (2018). link