4.2. Standard input files for DSQSS/DLA¶
In the standard model of DSQSS/DLA, users can define their own models and lattices. Of course, they can be combined with predefined ones. Fig. 4.2 shows a workflow of the standard mode.
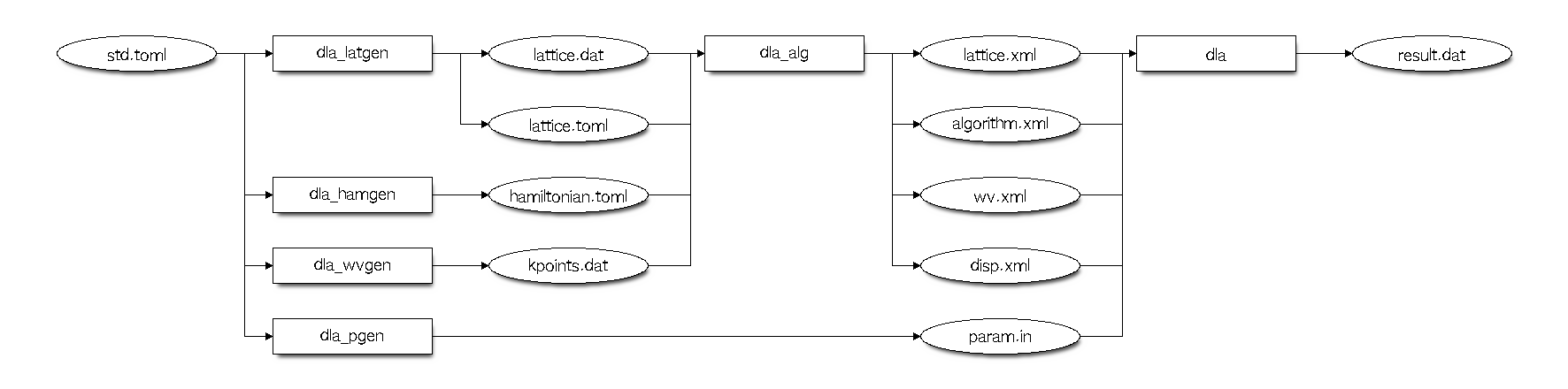
Fig. 4.2 Standard mode of DSQSS/DLA. Ellipses are files and rectangles are tools.¶
4.2.1. List of files¶
lattice.dat |
lattice datafile. |
lattice.toml |
lattice TOML file. |
hamiltonian.toml |
Hamiltonian TOML file. |
kpoints.dat |
Wavevector file. |
4.2.2. Lattice datafile¶
A lattice datafile is a textfile describing information of space (lattice), such as the number of sites and links connecting some sites.
This file is used as an input file of dla_alg.
From # mark to the end of the line is a comment and ignored.
A blank line is also ignored.
A “list” is written as space separated elements in one line like 2 2.
The lattice datafile includes the five sections,
name, lattice, directions, sites, interactions.
nameA string denoting the name of lattice. This is just a comment or a marker, and will not be used.
latticeThe section specifying general information of lattice.
- First line
An integer denoting dimension of the lattice.
- Second line
A list of integers denoting the size of the lattice.
- Third line
A list of integers denoting the boundary condition of the lattice.
1means the periodic boundary condition and0means the open one.
- Rest
A list of figures denoting the primitive translation vector \(\vec{e}^i\). The first integer means the index of the vector \(i\) and the rest floating point numbers mean coordinates of the vector in Cartesian, \(e_d^i\).
directionsThe section specifying directions of bonds (two-body interactions.)
- First line
An integer denoting the number of the directions.
- Rest
A list of figures denoting the a direction. The first integer means the index of the direction and the rest floating point numbers mean coordinates. The coordinates is represented by using the basis specified in
lattice.
sitesThe section specifying sites.
- First line
An integer denoting the number of the sites.
- Rest
A list of figures denoting a site. The first two integers mean the index and the type of the site, respectively. The rest floating point numbers mean the coordinates in the basis specified in
lattice.
interactionsThe section specifying interactions.
- First line
An integer denoting the number of the interactions.
- Rest
A list of \(N = \text{involved sites} + 5\) integers. The details are following.
column |
description |
|---|---|
1 |
The index of the interaction. |
2 |
The type of the interaction. |
3 |
The number of involved sites. |
4 … (N-2) |
The indices of the involved sites. |
N-1 |
If the bond crosses the boundary, this is 1. Otherwise, 0. |
N |
The index of the direction. |
The following is an example describing \(4 \times 4\) square lattice:
name
2 dimensional hypercubic lattice
lattice
2 # dim
4 4 # size
1 1 # 0:open boundary, 1:periodic boundary
0 1.0 0.0 # latvec_0
1 0.0 1.0 # latvec_1
directions
2 # ndirections
# id, coords...
0 1.0 0.0
1 0.0 1.0
sites
16 # nsites
# id, type, coord...
0 0 0 0
1 0 1 0
2 0 2 0
3 0 3 0
4 0 0 1
5 0 1 1
6 0 2 1
7 0 3 1
8 0 0 2
9 0 1 2
10 0 2 2
11 0 3 2
12 0 0 3
13 0 1 3
14 0 2 3
15 0 3 3
interactions
32 # nints
# id, type, nbody, sites..., edge_flag, direction
0 0 2 0 1 0 0
1 0 2 0 4 0 1
2 0 2 1 2 0 0
3 0 2 1 5 0 1
4 0 2 2 3 0 0
5 0 2 2 6 0 1
6 0 2 3 0 1 0
7 0 2 3 7 0 1
8 0 2 4 5 0 0
9 0 2 4 8 0 1
10 0 2 5 6 0 0
11 0 2 5 9 0 1
12 0 2 6 7 0 0
13 0 2 6 10 0 1
14 0 2 7 4 1 0
15 0 2 7 11 0 1
16 0 2 8 9 0 0
17 0 2 8 12 0 1
18 0 2 9 10 0 0
19 0 2 9 13 0 1
20 0 2 10 11 0 0
21 0 2 10 14 0 1
22 0 2 11 8 1 0
23 0 2 11 15 0 1
24 0 2 12 13 0 0
25 0 2 12 0 1 1
26 0 2 13 14 0 0
27 0 2 13 1 1 1
28 0 2 14 15 0 0
29 0 2 14 2 1 1
30 0 2 15 12 1 0
31 0 2 15 3 1 1
4.2.3. Lattice TOML file lattice.toml¶
A lattice TOML file is a TOML formatted file defining a lattice by using an unitcell and primitive translation vectors.
This is used as an input file of dla_alg.
This has two tables, parameter and unitcell.
parameterA table denoting general information of the lattice.
nameA string denoting the name of lattice.
dimAn integer denoting the dimension of lattice.
LAn array of integers denoting the size of lattice.
bcAn array of booleans denoting the boundary condition of lattice.
truemeans the periodic boundary condition andfalsemeans the open one.basisAn two-dimensional array (array of array) of floating point numbers denoting the primitive translation vectors.
unitcellA table describing a unitcell.
sitesAn array of tables denoting sites in one unitcell. One table corresponding one site.
siteidAn integer denoting the local index of the site in one unitcell.
typeAn integer denoting the type of the site.
coordAn array of floating point numbers denoting the coordinate of site in one unitcell.
bondsAn array of tables denoting bonds in one unitcell. One table corresponding one bond.
bondidAn integer denoting the local index of the bond in one unitcell.
typeAn integer denoting the type of the bond.
sourceA table denoting an end (source site) of the bond.
siteidAn integer denoting the local index of the source site.
targetA table denoting the other end (target site) of the bond.
siteidAn integer denoting the local index of the target site.
offsetAn array of integers denoting the relative coordinate of the unitcell where the target site belongs from the unitcell where the source site belongs.
The following is an example describing two dimensional square lattice.
[parameter]
name = "square lattice"
dim = 2
L = [4,4]
bc = [true, true]
basis = [[1,0], [0,1]]
[unitcell]
[[unitcell.sites]]
siteid = 0
type = 0
coord = [0,0]
[[unitcell.bonds]]
bondid = 0
type = 0
source = { siteid = 0 }
target = { siteid = 0, offset = [1,0] }
[[unitcell.bonds]]
bondid = 1
type = 0
source = { siteid = 0 }
target = { siteid = 0, offset = [0,1] }
4.2.4. Hamiltonian TOML file¶
A Hamiltonian TOML file is a TOML formatted file describing the local Hamiltonian.
This file is used as an input file of dla_alg.
A utility tool dla_hamgen generates Hamiltonian file for common models, XXZ spin model and Bose-Hubbard model.
nameA string denoting the name of the Hamiltonian.
sitesAn array of tables denoting the site Hamiltonians. One table corresponds to one type of site hamiltonian.
typeAn integer denoting the type of site Hamiltonian.
NAn integer denoting the number of states of the local degree of freedom. For example, for \(S=1/2\) spin this is 2.
valuesAn array of floating point numbers denoting the elements of local basis such as \(S^z\).
elementsAn array of tables denoting the elements of the Hamiltonian matrix. One table corresponds to one element.
istateAn integer denoting the index of the initial state (before the Hamiltonian acts on.)
fstateAn integer denoting the index of the final state (after the Hamiltonian acts on.)
valueA floating point number denoting the matrix element.
sourcesAn array of tables denoting the elements of the source Hamiltonian matrix, which is introduced to create and annihilate worm heads. One table corresponds to one element.
istateAn integer denoting the index of the initial state (before the Hamiltonian acts on.)
fstateAn integer denoting the index of the final state (after the Hamiltonian acts on.)
valueA floating point number denoting the matrix element.
interactionsAn array of tables denoting the many-body interaction Hamiltonians. One table corresponds to one type of interaction.
typeAn integer denoting the type of interaction.
nbodyAn integer denoting the number of involved sites.
NAn array of integers denoting the number of local states on the involved sites.
elementsAn array of tables denoting the elements of the Hamiltonian matrix. One table corresponds to one element.
istateAn array of integers denoting the index of the initial state (before the Hamiltonian acts on.)
fstateAn array of integers denoting the index of the final state (after the Hamiltonian acts on.)
valueA floating point number denoting the matrix element.
The following is an example describing \(S=1/2\) antiferromagnetic Heisenberg spin model
name = "S=1/2 XXZ model"
[[sites]]
id = 0
N = 2
values = [-0.5, 0.5]
[[sites.elements]]
istate = 0
fstate = 0
value = 0.5
[[sites.elements]]
istate = 1
fstate = 1
value = -0.5
[[sites.sources]]
istate = 0
fstate = 1
value = 0.5
[[sites.sources]]
istate = 1
fstate = 0
value = 0.5
[[interactions]]
id = 0
nbody = 2
N = [ 2, 2]
[[interactions.elements]]
istate = [ 0, 0]
fstate = [ 0, 0]
value = 0.25
[[interactions.elements]]
istate = [ 0, 1]
fstate = [ 0, 1]
value = -0.25
[[interactions.elements]]
istate = [ 0, 1]
fstate = [ 1, 0]
value = 0.5
[[interactions.elements]]
istate = [ 1, 0]
fstate = [ 1, 0]
value = -0.25
[[interactions.elements]]
istate = [ 1, 0]
fstate = [ 0, 1]
value = 0.5
[[interactions.elements]]
istate = [ 1, 1]
fstate = [ 1, 1]
value = 0.25
4.2.5. Wavevector datafile¶
A wavevector datafile is a textfile describing wavevectors
where \(\vec{g}\) is the set of the reciprocal vectors.
From # mark to the end of the line is a comment and ignored.
A blank line is also ignored.
A “list” is written as space separated elements in one line like 2 2.
The wavevector datafile includes the two sections, dim and kpoints.
dimAn integer denoting the dimension of the lattice.
kpointsA section describing wavevectors.
- First line
An integer denoting the number of wavevectors.
- Rest
A list of integers denoting the wavevector. The first integer means the index of the wavevector. The rest integers means the coordinates of the wavevector, \(k_d\).
Wavevectors are represented by using the reciprocal vectors \(\vec{g}\). When the coordinate of a lattice site is \(\vec{r} = \sum r_d \vec{e}_d\) and the wavevector is \(\vec{k} = \sum k_d \vec{g}_d\), the innerproduct of them is \(\vec{r}\cdot\vec{k} = \sum_d 2\pi r_d k_d / L_d\), where \(L_d\) is the length of the lattice along \(d\) th dimension.
The inner product between the coordinate \(\vec{r} = \sum r_d \vec{e}_d\) and the wavevector \(\vec{k} = \sum k_d \vec{g}_d\) is \(\vec{r}\cdot\vec{k} = \sum_d 2\pi r_d k_d / L_d\), where \(L_d\) is the size of lattice along \(d\) th dimension.
The following is an example of two dimensional case.
dim
2
kpoints
3
0 0 0
1 2 0
2 4 0
