ポピュレーションアニーリングによる探索¶
ここでは、ポピュレーションアニーリングを用いて、回折データから原子座標を解析する方法について説明します。
具体的な計算手順は minsearch の時と同様です。
サンプルファイルの場所¶
サンプルファイルは sample/sim-trhepd-rheed/single_beam/pamc にあります。
フォルダには以下のファイルが格納されています。
bulk.txtbulk.exeの入力ファイルexperiment.txt,template.txtメインプログラムでの計算を進めるための参照ファイル
ref.txt計算が正しく実行されたか確認するためのファイル(本チュートリアルを行うことで得られる
fx.txtの回答)。input.tomlメインプログラムの入力ファイル
prepare.sh,do.sh本チュートリアルを一括計算するために準備されたスクリプト
以下、これらのファイルについて説明したあと、実際の計算結果を紹介します。
参照ファイルの説明¶
template.txt , experiment.txt については、
前のチュートリアル(Nealder-Mead法による最適化)と同じものを使用します。
入力ファイルの説明¶
ここでは、メインプログラム用の入力ファイル input.toml について説明します。
input.toml の詳細については入力ファイルに記載されています。
以下は、サンプルファイルにある input.toml の中身になります。
[base]
dimension = 2
output_dir = "output"
[algorithm]
name = "pamc"
label_list = ["z1", "z2"]
seed = 12345
[algorithm.param]
min_list = [3.0, 3.0]
max_list = [6.0, 6.0]
unit_list = [0.3, 0.3]
[algorithm.pamc]
numsteps_annealing = 5
bmin = 0.0
bmax = 200.0
Tnum = 21
Tlogspace = false
nreplica_per_proc = 10
[solver]
name = "sim-trhepd-rheed"
[solver.config]
calculated_first_line = 5
calculated_last_line = 74
row_number = 2
[solver.param]
string_list = ["value_01", "value_02" ]
degree_max = 7.0
[solver.reference]
path = "experiment.txt"
first = 1
last = 70
ここではこの入力ファイルを簡単に説明します。 詳細は入力ファイルのレファレンスを参照してください。
[base] セクションはメインプログラム全体のパラメータです。
dimension は最適化したい変数の個数で、今の場合は2つの変数の最適化を行うので、2 を指定します。
[algorithm] セクションは用いる探索アルゴリズムを設定します。
交換モンテカルロ法を用いる場合には、 name に "exchange" を指定します。
label_list は、value_0x (x=1,2) を出力する際につけるラベル名のリストです。
seed は擬似乱数生成器に与える種です。
[algorithm.param] サブセクションは、最適化したいパラメータの範囲などを指定します。
min_list は最小値、 max_list は最大値を示します。
unit_list はモンテカルロ更新の際の変化幅(ガウス分布の偏差)です。
[algorithm.pamc] サブセクションは、ポピュレーションアニーリングのハイパーパラメータを指定します。
numsteps_annealingで指定した回数のモンテカルロ更新の後に、逆温度を増やします (温度を下げます)。bmin,bmaxはそれぞれ逆温度の下限・上限です。Tnumは計算する温度・逆温度の点数です。Tlogspaceがtrueの場合、温度を対数空間で等分割しますnreplica_per_procはMPIプロセスひとつが受け持つ計算レプリカの数です。
[solver] セクションではメインプログラムの内部で使用するソルバーを指定します。
minsearch のチュートリアルを参照してください。
計算実行¶
最初にサンプルファイルが置いてあるフォルダへ移動します(以下、本ソフトウェアをダウンロードしたディレクトリ直下にいることを仮定します).
cd sample/sim-trhepd-rheed/pamc
順問題の時と同様に、 bulk.exe と surf.exe をコピーします。
cp ../../../../../sim-trhepd-rheed/src/TRHEPD/bulk.exe .
cp ../../../../../sim-trhepd-rheed/src/TRHEPD/surf.exe .
最初に bulk.exe を実行し、bulkP.b を作成します。
./bulk.exe
そのあとに、メインプログラムを実行します(計算時間は通常のPCで数秒程度で終わります)。
mpiexec -np 4 python3 ../../../../src/py2dmat_main.py input.toml | tee log.txt
ここではプロセス数4のMPI並列を用いた計算を行っています。
(Open MPI を用いる場合で、使えるコア数よりも要求プロセス数の方が多い時には、
mpiexec コマンドに --oversubscribed オプションを追加してください。)
実行すると、各ランクのフォルダが作成され、
温度ごとに、各モンテカルロステップで評価したパラメータおよび目的関数の値を記した trial_TXXX.txt ファイル(XXX は温度点の番号)と、
実際に採択されたパラメータを記した result_TXXX.txt ファイル、さらにそれぞれを結合した trial.txt, result.txt ファイルが生成されます。
それぞれ書式は同じで、最初の2列がステップ数とプロセス内のwalker (replica) 番号、次が(逆)温度、3列目が目的関数の値、4列目以降がパラメータです。
最後の2 列は、 walker の重み (Neal-Jarzynski weight) と祖先(計算を開始したときのレプリカ)の番号です。
# step walker beta fx z1 z2 weight ancestor
0 0 0.0 0.07702743614780189 5.788848278451443 3.949126663745358 1.0 0
0 1 0.0 0.08737730661436376 3.551756435031283 3.6136808356591192 1.0 1
0 2 0.0 0.04954470587051104 4.70317508724506 4.786634108937754 1.0 2
0 3 0.0 0.04671675601156148 5.893543559206865 4.959531290614713 1.0 3
0 4 0.0 0.04142014655238446 5.246719912601735 4.960709612555206 1.0 4
また、 sim-trhepd-rheed ソルバーの場合は、 各作業フォルダの下にサブフォルダ Log%%%%% ( %%%%% がグリッドのid)が作成され、ロッキングカーブの情報などが記録されます
(各プロセスにおけるモンテカルロステップ数がidとして割り振られます)。
best_result.txt に、目的関数 (R-factor) が最小となったパラメータとそれを得たランク、モンテカルロステップの情報が書き込まれます。
nprocs = 4
rank = 0
step = 71
walker = 5
fx = 0.008186713312593607
z1 = 4.225633749839847
z2 = 5.142666117413409
最後に、 fx.txt には、各温度ごとの統計情報が記録されます。
# $1: 1/T
# $2: mean of f(x)
# $3: standard error of f(x)
# $4: number of replicas
# $5: log(Z/Z0)
# $6: acceptance ratio
0.0 0.06428002079611472 0.002703413400677839 40 0.0 0.795
10.0 0.061399304916174735 0.002649424392996749 40 -0.6280819199879947 0.85
20.0 0.05904248889111052 0.0031622711212952034 40 -1.2283060742855603 0.74
30.0 0.04956921148431115 0.0028298565759159633 40 -1.7991035905899855 0.67
1列目は温度・逆温度で、2・3列目は目的関数 \(f(x)\) の期待値と標準誤差、4列目はレプリカの個数、5列目は分配関数の比の対数 \(\log(Z_n/Z_0)\) です(\(Z_0\) は最初の温度点における分配関数)、6列目はモンテカルロ更新の採択率です。
なお、一括計算するスクリプトとして do.sh を用意しています。
do.sh では res.txt と ref.txt の差分も比較しています。
以下、説明は割愛しますが、その中身を掲載します。
sh prepare.sh
./bulk.exe
time mpiexec --oversubscribe -np 4 python3 ../../../../src/py2dmat_main.py input.toml
echo diff output/fx.txt ref.txt
res=0
diff output/fx.txt ref.txt || res=$?
if [ $res -eq 0 ]; then
echo TEST PASS
true
else
echo TEST FAILED: output/fx.txt and ref.txt differ
false
fi
計算結果の可視化¶
result_T%.txt を図示することで、 R-factor の小さいパラメータがどこにあるかを推定することができます。
今回の場合は、以下のコマンドをうつことで2次元パラメータ空間の図 result_fx.pdf と result_T.pdf が作成されます。
シンボルの色はそれぞれ R-factor と逆温度 \(\beta\) に対応します。
python3 plot_result_2d.py
作成された図を見ると、(5.25, 4.25) と (4.25, 5.25) 付近にサンプルが集中していることと、
R-factor の値が小さいことがわかります。
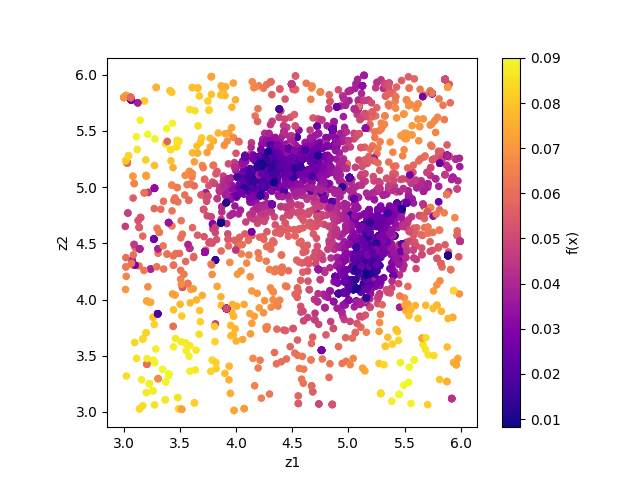
サンプルされたパラメータ。横軸は value_01 , 縦軸は value_02 を、色は R-factor を表す。¶
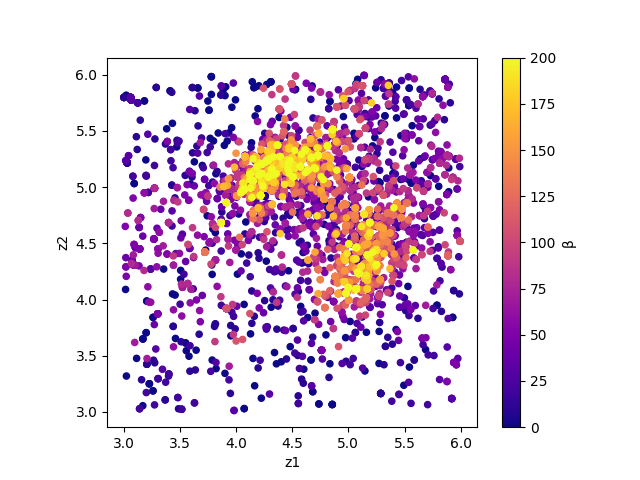
サンプルされたパラメータと逆温度。横軸は value_01 , 縦軸は value_02 を、色は逆温度を表す。¶
また、 RockingCurve.txt が各サブフォルダに格納されています。
LogXXX_YYY の XXX はモンテカルロのステップ数、 YYY は各MPIプロセス内のレプリカの番号です。
これを用いることで、前チュートリアルの手順に従い、実験値との比較も行うことが可能です。