Random search¶
In this section, we will explain how to perform a random search and analyze the minimization problem of Himmelblau function.
The random search is effective when it is difficult to use other methods such as grid search for high-dimensional problems.
The random search is compatible with MPI. The specific calculation procedure is the same as for minsearch.
Location of the sample files¶
The sample files are located in sample/analytical/random_search.
The following files are stored in the folder
input.tomlInput file of the main program.
plot_colormap_2d.pyProgram to visualize the calculation results.
do.shScript prepared for bulk calculation of this tutorial.
Input file¶
This section describes the input file for the main program, input.toml.
The details of input.toml can be found in the input file section of the manual.
[base]
dimension = 2
output_dir = "output"
[solver]
name = "analytical"
function_name = "himmelblau"
[runner]
[runner.log]
interval = 20
[algorithm]
name = "random_search"
seed = 12345
[algorithm.param]
max_list = [6.0, 6.0]
min_list = [-6.0, -6.0]
num_points = 100
The contents of [base], [solver], and [runner] sections are the same as those for the search by the Nelder-Mead method (minsearch).
[algorithm] section specifies the algorithm to use and its settings.
nameis the name of the algorithm you want to use. In this tutorial we will userandom_searchsince we will be using random-search method.
In [algorithm.param] section, the parameters for the search are specified.
min_listandmax_listare the minimum and the maximum values of each parameter.num_pointsspecifies the number of points along each parameter.
In this example, 100 points of parameters \((x_1, x_2)\) are generated randomly in the range \(-6.0 \leq x_1 \leq 6.0\), \(-6.0 \leq x_2 \leq 6.0\) and the function values are evaluated.
Calculation execution¶
First, move to the folder where the sample files are located. (We assume that you are directly under the directory where you downloaded this software.)
$ cd sample/analytical/minsearch
The, run the main program. The computation time takes only a few seconds on a normal PC.
$ mpiexec -np 4 python3 ../../../src/odatse_main.py input.toml | tee log.txt
Here, the calculation using MPI parallel with 4 processes will be done.
When executed, a folder for each rank will be created under output directory, and the calculation results of each rank will be written.
The standard output will be seen like this.
Make ColorMap
Iteration : 1/100
Iteration : 2/100
Iteration : 3/100
Iteration : 4/100
Iteration : 5/100
Iteration : 6/100
Iteration : 7/100
...
Finally, the function values calculated for all the points randomly generated will be written to output/ColorMap.txt.
In this case, the following results will be obtained.
5.155393 -2.203493 187.944291
-3.792974 -3.545277 3.179381
0.812700 1.146536 108.254643
5.574174 1.838125 483.841834
2.986880 1.842838 0.436331
2.972578 5.535681 719.799258
-5.899340 -4.722667 452.469102
-2.415555 1.876934 45.535582
3.717751 4.466111 330.797237
5.575771 2.684224 552.047948
...
The first and second columns contain the values of x1 and x2, and the third column contains the function value.
Visualization of calculation results¶
By plotting ColorMap.txt, we can estimate the region where the small function values are located.
A program plot_colormap_2d.py is prepared to generate such a plot of the two-dimensional space.
$ python3 plot_colormap_2d.py
By executing the above command, ColorMapFig.png is generated in which the functional value evaluated at each point is shown as a color map on top of the contour of Himmelblau function.
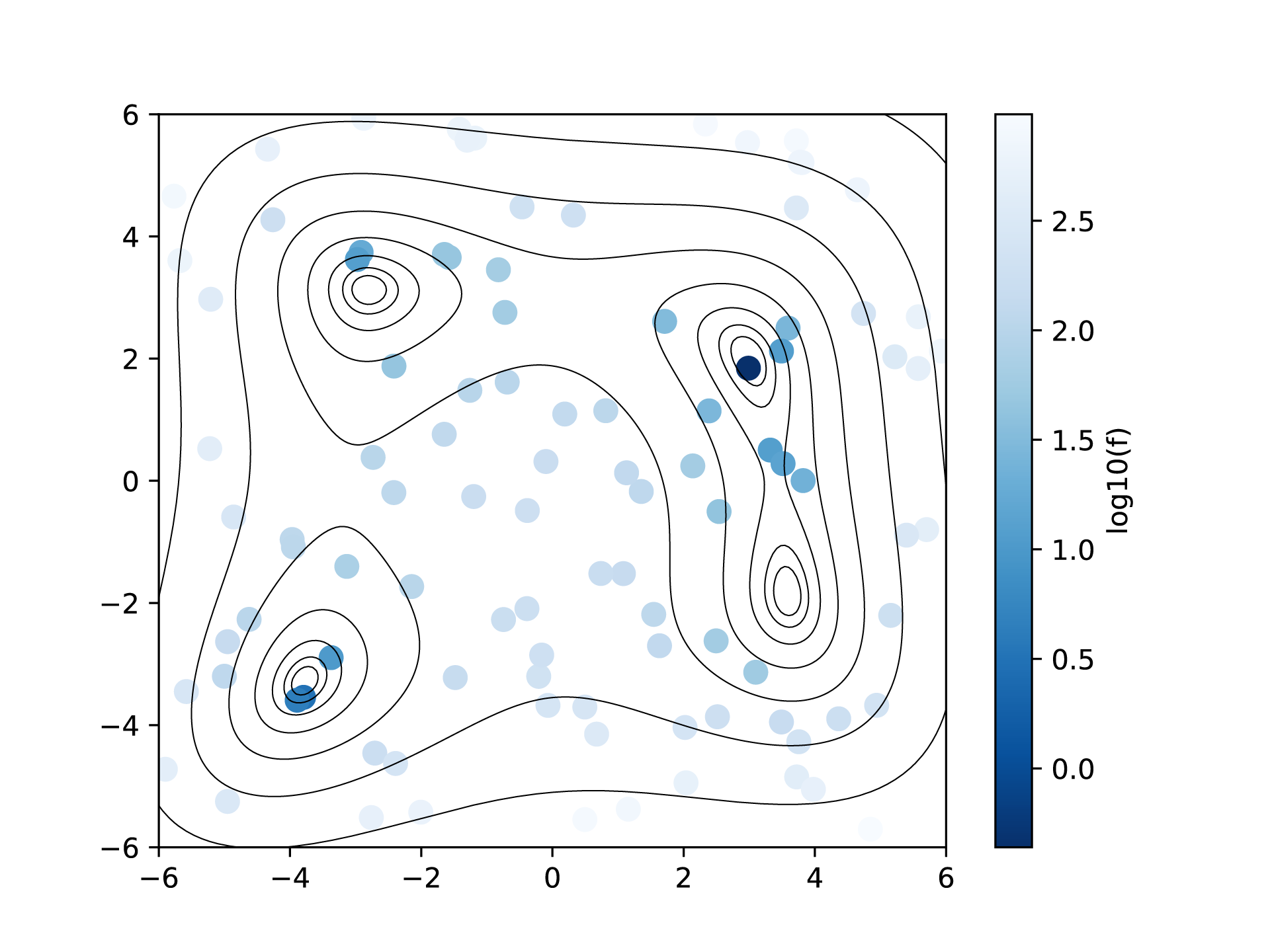
Fig. 4 Color map of the function values in the random search of the two-dimensional parameter space.¶