4.3. Magnetic Susceptibility of antiferromagnetic spin chains

In this tutorial, we will calculate the temperature dependence of the magnetic susceptibility for two kinds of antiferromagnetic spin chains with the local spin length \(S=1/2, 1\).

The following Python script (sample/dla/02_spinchain/exec.py) performs DSQSS/DLA work-flow for each parameter (combination of spin length and temperature) automatically.

import sys
import os.path
import subprocess

bindir = sys.argv[1] if len(sys.argv) > 1 else ''

name = 'xmzu'
Ms = [1,2]
Ts = [0.05, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0, 1.25, 1.5, 1.75, 2.0]

for M in Ms:
    output = open('{}_{}.dat'.format(name,M), 'w')
    for i,T in enumerate(Ts):
        with open('std_{}_{}.in'.format(M,i), 'w') as f:
            f.write('''
    solver = DLA
    model_type = spin
    J = -1
    F = 0.0
    lattice_type = square
    D = 1
    L = 30
    nset = 5
    ntherm = 1000
    ndecor = 1000
    nmcs = 1000
    ''')
            f.write('M = {}\n'.format(M))
            f.write('beta = {}\n'.format(1.0/T))
            f.write('outfile = res_{}_{}.dat\n'.format(M,i))
        cmd = [os.path.join(bindir, 'dsqss_pre.py'),
               '-p', 'param_{}_{}.in'.format(M,i),
               '-i', 'std_{}_{}.in'.format(M,i)]
        subprocess.call(cmd)
        cmd = [os.path.join(bindir, 'dla_H'), 'param_{}_{}.in'.format(M,i)]
        subprocess.call(cmd)
        with open('res_{}_{}.dat'.format(M,i)) as f:
            for line in f:
                if not line.startswith('R'):
                    continue
                words = line.split()
                if words[1] == name:
                    output.write('{} {} {}\n'.format(T, words[3], words[4]))

This script receives the binary directory as an argument (if an environment variable $DSQSS_ROOT is set correctly, the argument can be omitted).

$ python exec.py $DSQSS_ROOT/bin

The result of \(S=1/2,1\) will be written to xmzu_1.dat and xmzu_2.dat, respectively (Fig. 4.1). The \(S=1/2\) chain is gapless and so the magnetic susceptibility remains finite at absolute zero (note that in the simulation the finite size effect opens energy gap). On the other hand the magnetic susceptibility of the \(S=1\) chain drops to zero at finite temperature due to the spin gap.

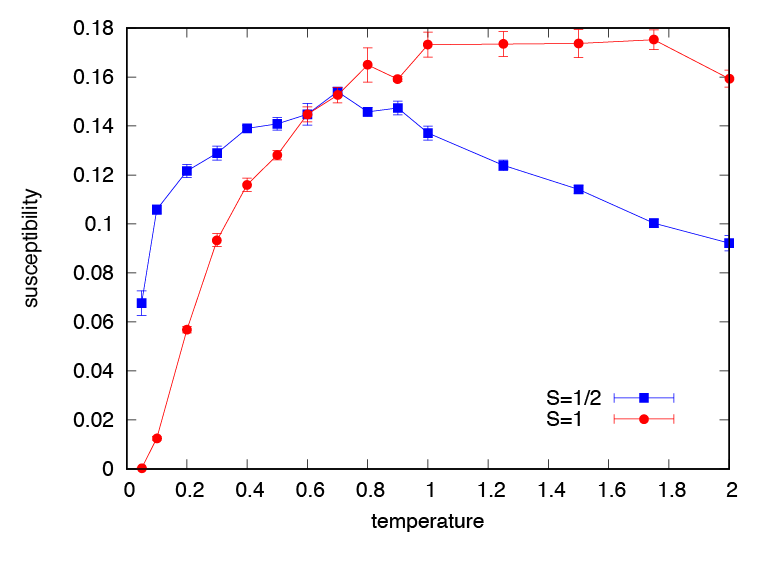
Fig. 4.1 Temperature v.s. susceptibility curves for \(S=1/2\) (blue) and \(S=1\) (red) antiferromagnetic Heisenberg chain.