4.3. Finite Temperature Calculations for the Transverse Field Ising Model

In this section, we present a calculation example of the ferromagnetic Ising model on a square lattice subjected to a transverse magnetic field, denoted by hx, at finite temperatures. The Hamiltonian is

\[\begin{aligned} H = J^z \sum_{\langle i,j \rangle} {S}_i^{z} {S}_j^{z} - h^x \sum_i S_i^x. \end{aligned}\]

Please note that the model is defined using spin operators of size 1/2, not Pauli operators. The input and script files used in this tutorial are located in the sample/03_finite_temperature directory. Below is a sample input file (simple_ft_strong.toml):

[parameter]
[parameter.general]
mode = "finite"
is_real = false
output = "output_ft_strong"
measure_interval = [10, 10, 5]

[parameter.simple_update]
num_step = [50, 200, 10]
tau = [0.01, 0.005, 0.05]

[parameter.full_update]
num_step = 0
tau = 0.0

[parameter.ctm]
iteration_max = 10
dimension = 10

[lattice]
type = "square lattice"
L = 2
W = 2
virtual_dim = 3

[model]
type = "spin"
Jz = -1.0
Jx = 0.0
Jy = 0.0
hx = 2.0

To perform finite temperature calculations, set the mode to finite. Here, the transverse magnetic field is set to hx = 2.0 with tau = 0.01 (the inverse temperature step size is 2 times tau). Once preparing an input file of the simple mode, execute tenes_simple, tenes_std, and tenes in the same way as for the ground state calculation.

The results of the finite temperature calculations are output to the output_ft_strong directory. Basically, the output is the same as the ground state calculation, but the inverse temperature is added to the first column. For example, FT_density.dat is as follows:

# The meaning of each column is the following:
# $1: inverse temperature
# $2: observable ID
# $3: real
# $4: imag
# The meaning of observable IDs are the following:
# 0: Energy
# 1: Sz
# 2: Sx
# 3: Sy
# 4: bond_hamiltonian
# 5: SzSz
# 6: SxSx
# 7: SySy

0.00000000000000000e+00 0  0.00000000000000000e+00  0.00000000000000000e+00
0.00000000000000000e+00 1  0.00000000000000000e+00  0.00000000000000000e+00
0.00000000000000000e+00 2  0.00000000000000000e+00  0.00000000000000000e+00
0.00000000000000000e+00 3  0.00000000000000000e+00  0.00000000000000000e+00
0.00000000000000000e+00 4  0.00000000000000000e+00  0.00000000000000000e+00
0.00000000000000000e+00 5  0.00000000000000000e+00  0.00000000000000000e+00
0.00000000000000000e+00 6  0.00000000000000000e+00  0.00000000000000000e+00
0.00000000000000000e+00 7  0.00000000000000000e+00  0.00000000000000000e+00

   ... continued ...

The second column indicates the type of physical quantity, and for example, 0 represents energy. Thus, you can extract the temperature dependence by extracting only the energy with awk:

awk '$2 == 0 {print $1, $3, $4}' output_ft_strong/FT_density.dat > energy_strong.dat

To observe the behavior at different transverse magnetic fields, we’ve provided additional sample input files: simple_ft_middle.toml (hx = 0.8), simple_te_weak.toml (hx = 0.5), and simple_ft_zero.toml (hx = 0.0). Moreover, a script named run.sh has been set up to execute all these calculations simultaneously. Ensure you’ve added tools like tenes to your PATH, then initiate the calculations with:

sh run.sh

The computation should complete in about a minute. Since specific heat is difficult to calculate directly, it is calculated from the energy by numerical differentiation. calcspec.py is a script to calculate specific heat from the energy by using the spline interpolation:

python3 calcspec.py

To visualize the results, scripts have been prepared to plot energy, heat capacity, and magnetization (\(S_x\), \(S_z\)): plot_e.plt, plot_c.plt, plot_mx.plt, and plot_mz.plt. Running the following:

gnuplot -persist plot_e.plt
gnuplot -persist plot_c.plt
gnuplot -persist plot_mx.plt
gnuplot -persist plot_mz.plt

will display plots for energy, heat capacity, and magnetizations (\(m_x\) and \(m_z\)). The resulting plots are illustrated in Fig. 4.4. For comparison, results obtained using Quantum Monte Carlo calculations are also shown (using ALPS/looper).

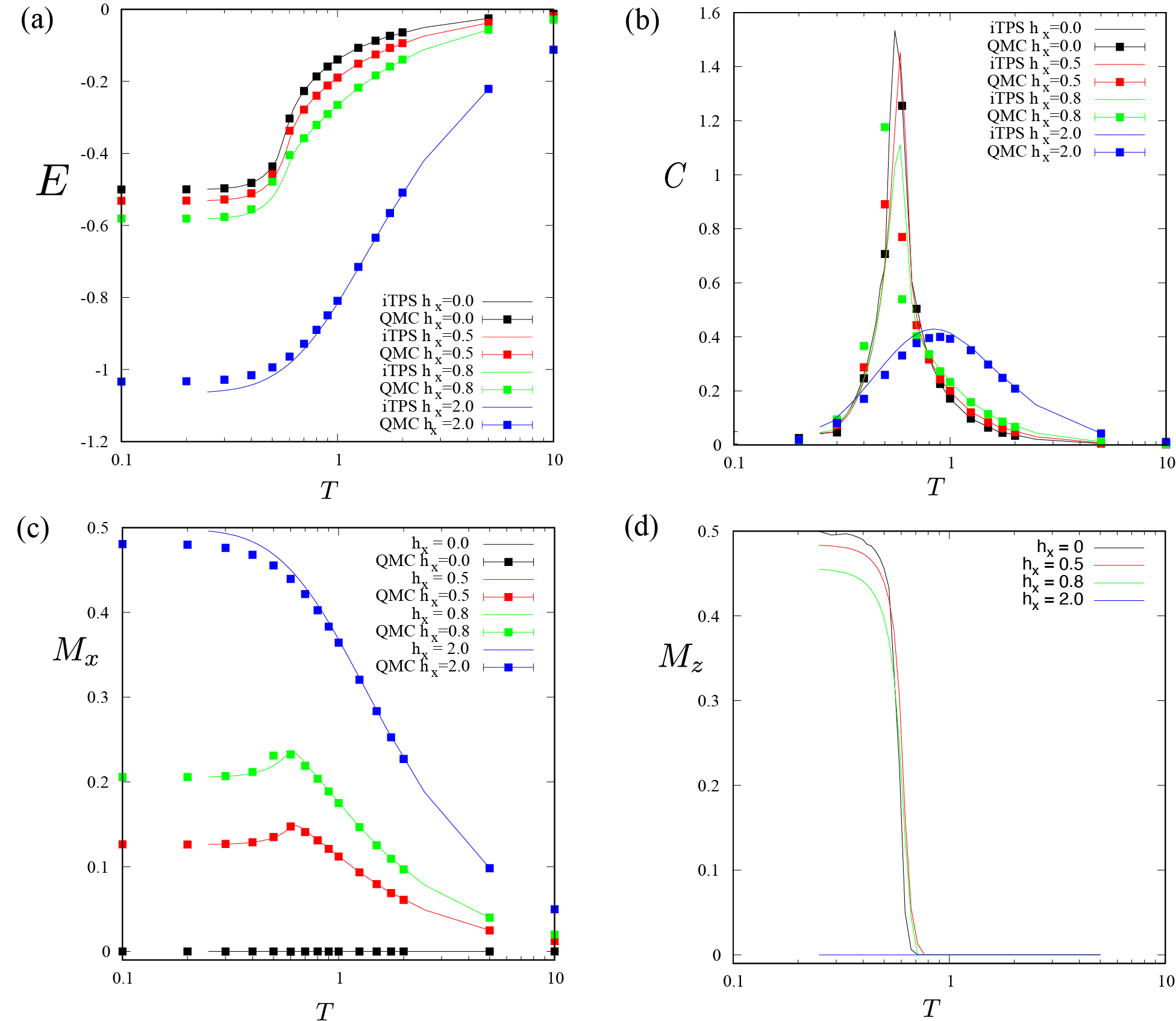
Fig. 4.4 Graphs for the finite temperature calculations of the Ising model: (a) energy, (b) heat capacity, (c) \(m_x\), and (d) \(m_z\). The vertical axis represents the physical quantity, and the horizontal axis denotes temperature.