4.2. DSQSS/DLA のスタンダードモード¶
DSQSS/DLA のスタンダードモードでは, ユーザが模型や格子を定義して計算することができます. あらかじめ定義された模型や格子と組み合わせたり, 拡張することも可能です. 図 4.1 はスタンダードモードによる計算の流れ図です.
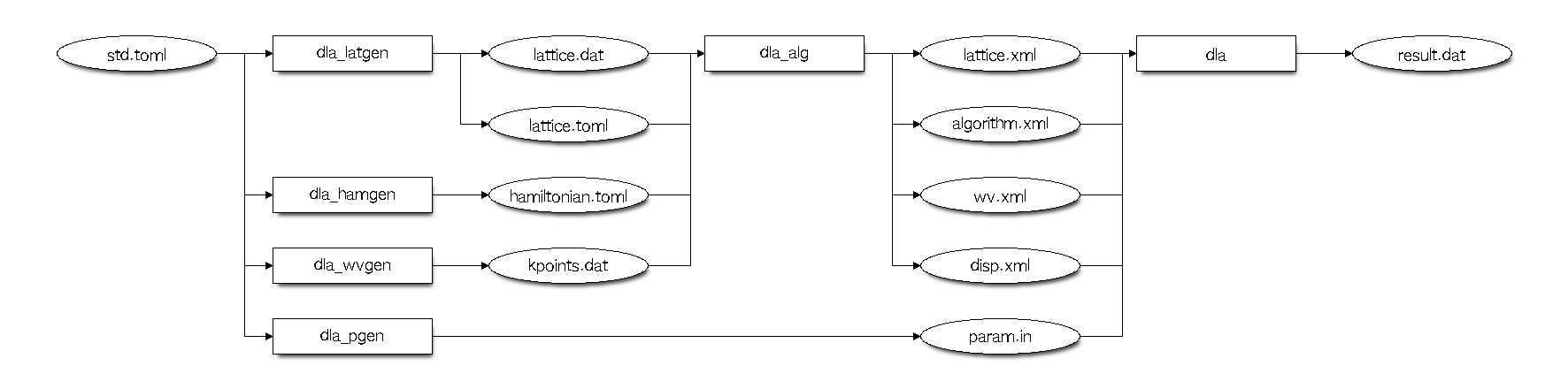
図 4.2 DSQSS/DLA のスタンダードモード. 丸囲みがファイルを, 四角囲みがツールを表す.¶
4.2.1. 入力ファイル一覧¶
lattice.dat |
格子datファイル. |
lattice.toml |
格子TOMLファイル. 格子ファイルはどちらか一方があればよい. |
hamiltonian.toml |
ハミルトニアンTOMLファイル. |
kpoints.dat |
波数ファイル. |
4.2.2. 格子データファイル¶
格子データファイルは空間の情報, たとえばサイトの数やサイト同士のつながりかたなどを定義するためのテキストファイルです.
dla_alg の入力ファイルとして扱われます.
# から行末まではコメントとして読み飛ばされます. また, 空白行も飛ばされます.
name, lattice, directions, sites, interactions の5つのセクションから構成されます.
name格子の名前です. 1行のテキストからなります. コメントや識別用であり, 実際の計算では利用されません.
lattice格子の情報を指定するセクションです.
- 1行目
格子の次元を表す整数.
- 2行目
格子のサイズを表す, 空白区切りで次元の数だけ並べられた整数の組.
- 3行目
格子の境界条件を表す, 空白区切りで次元の数だけ並べられた整数の組. 1 で周期的境界条件を, 0 で開放端境界条件を示します.
- 4行目以降
空間の基底ベクトル \(\vec{e}^i\) を表す, 空白区切りで次元の数+1 だけ並べられた数の組. 最初の整数はベクトルの番号 \(i\) を, 残りの数はベクトルのデカルト座標 \(e_d^i\) を示します.
directionsボンド(二体相互作用)の向きを指定するセクションです.
- 1行目
ボンドの向きの総数.
- 2行目以降
各向きを表すベクトルを表す, 空白区切りで次元の数+1 だけ並べられた数の組. 最初の整数は向きの番号を, 残りの数はベクトルの要素を示します.
latticeで指定されたベクトルを基底とします.
sitesサイトの情報を指定するセクションです.
- 1行目
格子に含まれるサイトの総数を表す整数.
- 2行目以降
各サイトの情報を表す空白区切りで次元の数+2 だけ並べられた数の組. 意味は次表の通り.
列 |
説明 |
|---|---|
1 |
サイト番号. 格子全体における通し番号. |
2 |
サイトタイプ. ハミルトニアンTOML ファイルにおけるサイトタイプと対応する. |
3 ... |
|
interactions相互作用の空間情報を指定するセクションです.
- 1行目
格子に含まれる多体相互作用の総数を表す整数.
- 2行目以降
\(N = \text{関与サイト数} + 5\) 個の整数の組. 意味は次表の通り.
列 |
説明 |
|---|---|
1 |
相互作用番号. 格子全体における通し番号. |
2 |
相互作用タイプ. ハミルトニアン TOML ファイルにおける相互作用タイプと対応する. |
3 |
関与サイト数 |
4 ... (N-2) |
サイト番号 |
N-1 |
ボンドが周期境界をまたぐ場合には1, そうでなければ0 |
N |
ボンドの方向番号 |
二次元正方格子の例を示します.
name
2 dimensional hypercubic lattice
lattice
2 # dim
4 4 # size
1 1 # 0:open boundary, 1:periodic boundary
0 1.0 0.0 # latvec_0
1 0.0 1.0 # latvec_1
directions
2 # ndirections
# id, coords...
0 1.0 0.0
1 0.0 1.0
sites
16 # nsites
# id, type, coord...
0 0 0 0
1 0 1 0
2 0 2 0
3 0 3 0
4 0 0 1
5 0 1 1
6 0 2 1
7 0 3 1
8 0 0 2
9 0 1 2
10 0 2 2
11 0 3 2
12 0 0 3
13 0 1 3
14 0 2 3
15 0 3 3
interactions
32 # nints
# id, type, nbody, sites..., edge_flag, direction
0 0 2 0 1 0 0
1 0 2 0 4 0 1
2 0 2 1 2 0 0
3 0 2 1 5 0 1
4 0 2 2 3 0 0
5 0 2 2 6 0 1
6 0 2 3 0 1 0
7 0 2 3 7 0 1
8 0 2 4 5 0 0
9 0 2 4 8 0 1
10 0 2 5 6 0 0
11 0 2 5 9 0 1
12 0 2 6 7 0 0
13 0 2 6 10 0 1
14 0 2 7 4 1 0
15 0 2 7 11 0 1
16 0 2 8 9 0 0
17 0 2 8 12 0 1
18 0 2 9 10 0 0
19 0 2 9 13 0 1
20 0 2 10 11 0 0
21 0 2 10 14 0 1
22 0 2 11 8 1 0
23 0 2 11 15 0 1
24 0 2 12 13 0 0
25 0 2 12 0 1 1
26 0 2 13 14 0 0
27 0 2 13 1 1 1
28 0 2 14 15 0 0
29 0 2 14 2 1 1
30 0 2 15 12 1 0
31 0 2 15 3 1 1
4.2.3. 格子TOML ファイル¶
格子TOML ファイルはユニットセルと基本並進ベクトルを用いて空間の情報を定義するための,
TOML 形式のファイルです.
dla_alg の入力ファイルとして扱われます.
parameter と unitcell のふたつのテーブルから構成されます.
parameter格子の情報を記述するテーブルです.
name格子の名前です. 実際の計算には用いられません.
dim格子の空間次元を表す整数です.
L格子の大きさを表す整数配列です.
bc格子の境界条件を表すブーリアンの配列です.
trueが周期的境界条件を,falseが開放端境界条件を示します.basis格子の基本並進ベクトルを表す2次元配列(配列の配列)です.
unitcellユニットセルの情報を記述するテーブルです.
sitesユニットセル内のサイトを示すテーブルの配列です.
siteidサイトのユニットセル内での識別番号です.
typeサイトタイプを示す整数です.
coordユニットセル内におけるサイトの局所座標を示す配列です.
bondsユニットセル内のボンドを示すテーブルの配列です.
bondidボンドのユニットセル内での識別番号です.
type相互作用タイプを示す整数です.
sourceボンドの始点サイトの情報を表すテーブルです.
siteidサイトのユニットセル内での識別番号です.
targetボンドの終点サイトの情報を表すテーブルです.
siteidサイトのユニットセル内での識別番号です.
offset始点サイトの属するユニットセルから見た, 終点サイトの属するユニットセルの相対座標です.
二次元正方格子の例を示します.
[parameter]
name = "square lattice"
dim = 2
L = [4,4]
bc = [true, true]
basis = [[1,0], [0,1]]
[unitcell]
[[unitcell.sites]]
siteid = 0
type = 0
coord = [0,0]
[[unitcell.bonds]]
bondid = 0
type = 0
source = { siteid = 0 }
target = { siteid = 0, offset = [1,0] }
[[unitcell.bonds]]
bondid = 1
type = 0
source = { siteid = 0 }
target = { siteid = 0, offset = [0,1] }
4.2.4. ハミルトニアンTOMLファイル¶
ハミルトニアンTOMLファイルは局所ハミルトニアン, 例えばボンドハミルトニアン, を指定する,
TOML 形式で記述されるテキストファイルです.
dla_alg の入力として, アルゴリズム定義ファイルを作成するために用いる補助入力ファイルとなっています.
ハイゼンベルグ模型などのよく用いられる模型については,
補助ツール dla_hamgen が用意されています.
nameハミルトニアンの名前です. シミュレーション中で使われることはありません.
sitesサイトハミルトニアンの情報を記述するテーブルの配列です.
typeサイトタイプを示す整数です.
N局所自由度が取りうる状態の数を示す整数です. 例えば \(S=1/2\) スピンでは 2 です.
values局所自由度の基底演算子の対角要素. 例えば \(S=1/2\) スピンでは
[-0.5, 0.5].elementsサイトハミルトニアンの行列要素を示すテーブルの配列です.
istateハミルトニアンが作用する前のサイトの状態番号です.
fstateハミルトニアンが作用した後のサイトの状態番号です.
valueハミルトニアンの行列要素の値です.
sourcesワームを導入するためのソースハミルトニアンの行列要素を示すテーブルの配列です.
istateハミルトニアンが作用する前のサイトの状態番号です.
fstateハミルトニアンが作用した後のサイトの状態番号です.
valueハミルトニアンの行列要素の値です.
interactions多体相互作用の情報を記述するテーブルの配列です.
type相互作用タイプを示す整数です.
nbody相互作用に関与するサイトの数を示す整数です.
N相互作用に関与するサイトそれぞれで, 局所自由度が取りうる状態の数です. 整数の配列で指定します.
elements相互作用ハミルトニアンの行列要素を記述するテーブルの配列です.
istate相互作用ハミルトニアンが作用する前のサイトの状態を指定する整数の配列です.
fstate相互作用ハミルトニアンが作用した後のサイトの状態を指定する整数の配列です.
value相互作用ハミルトニアンの行列要素の値です.
\(S=1/2\) 反強磁性ハイゼンベルグ模型の例を示します.
name = "S=1/2 XXZ model"
[[sites]]
id = 0
N = 2
[[sites.elements]]
istate = 0
fstate = 0
value = 0.5
[[sites.elements]]
istate = 1
fstate = 1
value = -0.5
[[sites.sources]]
istate = 0
fstate = 1
value = 0.5
[[sites.sources]]
istate = 1
fstate = 0
value = 0.5
[[interactions]]
id = 0
nbody = 2
N = [ 2, 2]
[[interactions.elements]]
istate = [ 0, 0]
fstate = [ 0, 0]
value = 0.25
[[interactions.elements]]
istate = [ 0, 1]
fstate = [ 0, 1]
value = -0.25
[[interactions.elements]]
istate = [ 0, 1]
fstate = [ 1, 0]
value = 0.5
[[interactions.elements]]
istate = [ 1, 0]
fstate = [ 1, 0]
value = -0.25
[[interactions.elements]]
istate = [ 1, 0]
fstate = [ 0, 1]
value = 0.5
[[interactions.elements]]
istate = [ 1, 1]
fstate = [ 1, 1]
value = 0.25
4.2.5. 波数ファイル¶
波数ファイルは, 波数ベクトル
の \(\vec{n}^{(i)}\) を指定するテキストファイルです.
dim格子の次元を示す整数です.
kpoints波数ベクトルを指定するセクションです.
- 1行目
波数ベクトルの総数.
- 2行目以降
波数ベクトルを表す, 空白区切りで次元の数+1 だけ並べられた数の組. 最初の整数は波数ベクトルの番号を, 残りの数はベクトルの要素 \(k_d\) を示します.
ベクトルの基底は逆格子ベクトル \(\vec{g}\) です. 格子の座標が \(\vec{r} = \sum r_d \vec{e}_d\) で表現されて, 波数が \(\vec{k} = \sum k_d \vec{g}_d\) で表現されているとき, これらの内積は \(\vec{r}\cdot\vec{k} = \sum_d 2\pi r_d k_d / L_d\) となります. ここで \(L_d\) は \(d\) 番目の次元における格子のサイズです.
二次元の例を示します.
dim
2
kpoints
3
0 0 0
1 2 0
2 4 0
