8. アルゴリズム

abICSは、拡張アンサンブル法と任意のエネルギー計算ソフトウェアを組み合わせるために設計されています。現在は、 レプリカ交換モンテカルロ法およびポピュレーションアニーリングモンテカルロ法が実装されています。

8.1. レプリカ交換モンテカルロ法

広く使用されているメトロポリスモンテカルロ法は、局所安定配置に捕まりやすく、そこでサンプリングが行き詰まる傾向があります。 レプリカ交換法は、計算対象の系のコピー（レプリカ）を使って、この問題を克服することを目的としています。 レプリカ交換法は、大まかに次のように説明できます（より正確な説明については、下記の文献を参照してください）。 まず、各レプリカに対して異なる温度におけるモンテカルロサンプリングを個別に実行します。 事前に設定された任意の間隔で、メトロポリス基準に従ってレプリカ間で温度を交換し、サンプリングを再開します。 メトロポリス基準によって、大まかには、エネルギーが低いレプリカに低い温度が割り当てられることになります。 これにより、高い温度のレプリカによる大域的なサンプリングと低い温度における局所安定配置の探索を共存させることができます。

abICSでは、入力ファイルの [replica] セクションでレプリカ交換モンテカルロ法に関連したパラメータを指定します。 レプリカの温度の下限を \(T_s =\) kTstart 、 上限を \(T_e =\) kTend とし、レプリカ数を \(N_r =\) nreplicas とすることで、

\[T_i = \frac{T_e-T_s}{N_r-1} i + T_s\]

として \(N_r\) 個の異なる温度に接触しているレプリカ系が用意されます(ただし、 \(i=0 \cdots N_r-1\) 。abICSでは、 nprocs_per_replica を使用して、各レプリカで計算を実行する並列ソルバープロセスの数を指定できます)。 モンテカルロステップ数は nsteps で指定し、 RXtrial_frequency ステップ毎に交換遷移確率

\[R = \exp\left[-\left(\frac{1}{T_i}-\frac{1}{T_{k}}\right)\left(E(X_i)-E(X_{k})\right)\right]\]

が計算され、確率 \(R\) で温度交換 \(T_i \leftrightarrow T_{k}\) が行われます (ただし、 \(X_i\) はi番目のレプリカ系の状態です。また、abICSでは隣接する温度を持ったレプリカ同士で交換試行をしています)。 なお、物理量は sample_frequency ステップ毎に測定が行われます。

8.2. ポピュレーションアニーリングモンテカルロ法

基底状態を得るためのモンテカルロ法として、シミュレーテッドアニーリング (SA) 法が知られています。 これは、温度一定のもとモンテカルロサンプリングを行い、一定のモンテカルロステップ数を実行した後に温度を強制的に下げていく手法です。 はじめは高温での大域的な探索が行われ、シミュレーションが進むごとに低温化での局所安定配置の探索が行われます。 SA の難点として、温度変化時に熱平衡状態から離れてしまうために、カノニカル平均を取りたい場合には温度ごとに熱平衡化する必要があります。 この問題を克服した手法が Annealed Importance Sampling (AIS) です。 AIS では多数のレプリカを用いて並行してSA を行い、温度降下時のズレを付加的な重みとして取り入れます。 この重み(Neal-Jarzynski 重み)は、サンプル間の加重平均が温度ごとのカノニカル平均となるように適切に定義されます。 AIS では計算が進むごとに NJ重みのばらつきが大きくなり、一部のレプリカのみが平均に寄与する、言い換えれば実行的なレプリカ数が減っていくという問題があります。 そこで、出現頻度がNJ 重みに比例するようにレプリカを定期的にリサンプリングし、重みを1にリセットするのがポピュレーションアニーリングモンテカルロ(PAMC)です。

8.3. 配置と更新

ここでは、 図 8.1 を例にabICSでの格子配置の定義とモンテカルロ法での更新の概要を説明します。 (a)-(c)は unitcell 、 base_structure 、 defect_structure の概念図で、青丸、緑丸、黒丸はそれぞれ base_structure で定義される原子種、星印は defect_structure で定義される欠陥が入る位置を表します。 (d)は base_structure で原子種を指定する場合の概念図です。 ここでは、blue, green, blackの3原子種を定義しています。各原子がどのように配置されるかは、各原子種ごとに coords で定義します。 (e)は defect_structure で欠陥位置に入るグループを指定する場合の概念図です。 orange は2種の原子種から構成される4原子で構成されるグループを定義し、 purple は3種の原子種から構成される3原子のグループを構成しています。 defect_structure.coords で指定される欠陥位置にこれらのグループが配置されます。 各グループ内での原子の配置は defect_structure.groups セクション内の coords で指定できます。 defect_structure を複数定義した場合は、それぞれの欠陥座標にそれぞれの原子グループが配置されます。 (f) はモンテカルロ法のアップデートに関する概念図です。 アップデートでは欠陥の位置に入るグループを入れ替えるパターンと、配置は変えずに配位を変える2つのパターンがあります(どちらのアップデートを行うかは半分の確率で自動で選択されます)。提案された配置 \(X_{trial}\) から指定されたソルバーでエネルギーを計算し、採択率 \(P(X_i \rightarrow X_{trial})\) を計算します。

グランドカノニカルサンプリングを sampling.enable_grandcanonical パラメータで有効にした場合、上記の配置更新に加えて、欠陥位置に入る原子グループを熱浴と出し入れする配置更新パターンが導入されます。原子グループの数は共役なパラメータである化学ポテンシャル config.chemical_potential で規定され、各グループごとに増減させることも、複数グループを同時に増減させることも記述できます。 配置更新では、現在の配置と提案配置のエネルギー差を元に、採択確率

\[P(X_i\to X_\text{trial}) = \min\left( 1, \Delta W\,e^{-\beta(\Delta E - \mu \Delta N)} \right)\]

による Metropolis-Hastings 法に基づいて配置が更新されます。 \(\Delta W = Q(X_\text{trial}\to X_i)/Q(X_i\to X_\text{trial})\) は、配置 \(X\) から配置 \(X^\prime\) を選択する提案確率 \(Q(X\to X^\prime)\) に基づく重み因子です。

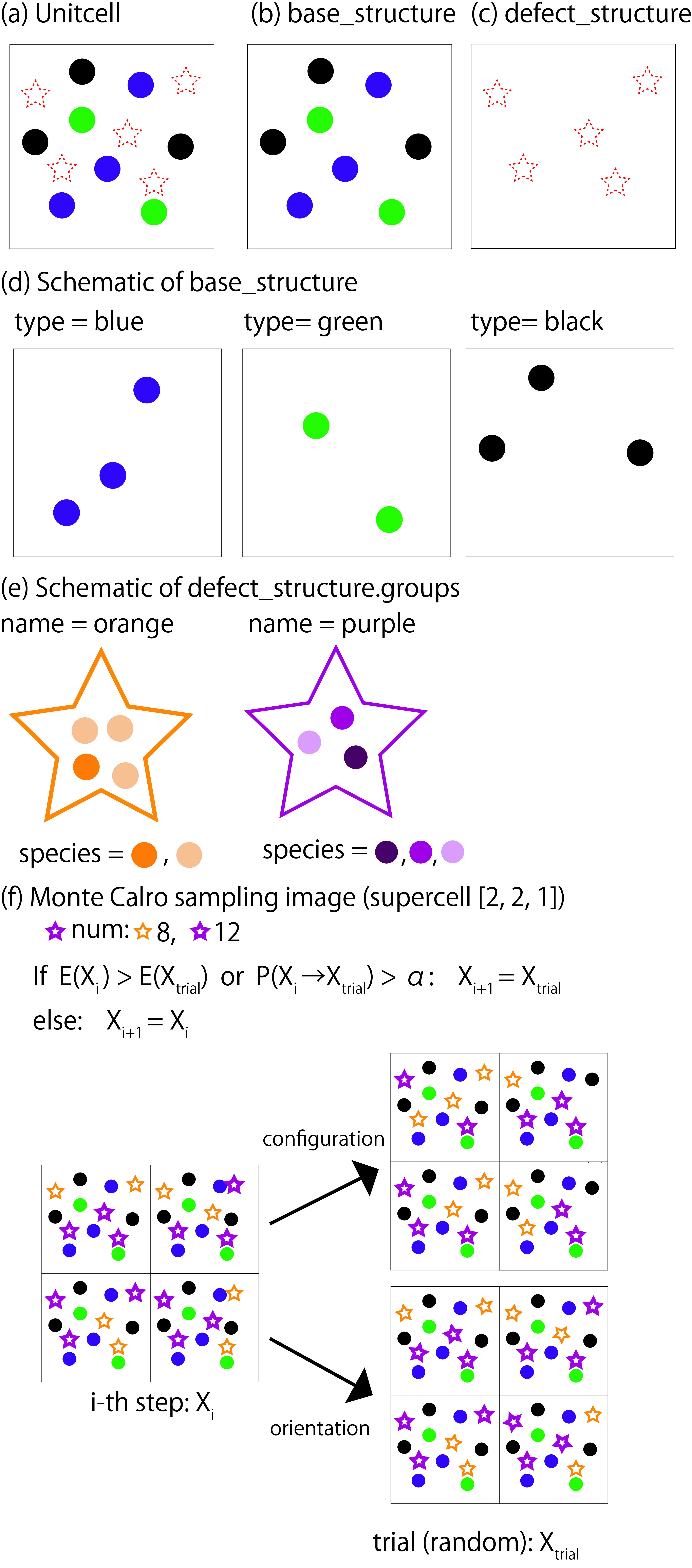
../_images/alg_sampling.png

図 8.1 (a)-(e)abICSでの格子の定義と(f)モンテカルロ法の概要。詳細は本文に記載。