This jupyter notebook file is available at ISSP Data Repository (develop branch).

Optimization in Continuous Space

In the tutorials so far, we have been discretizing the feature space to perform Bayesian optimization. PHYSBO can also optimize while keeping quantities continuous.

As an algorithm for maximizing the acquisition function in continuous space, random search is implemented. Additionally, you can use ODAT-SE as an optimization library. This can be installed using pip.

python3 -m pip install odatse

Basic Usage

First, import the necessary modules.

import numpy as np
import physbo
import matplotlib.pyplot as plt

The function simulator to be optimized, unlike the discrete version which received candidate point numbers action as input, in the continuous version directly receives coordinates x as input. x is an array of size \(N\times D\), where \(N\) is the number of data points to compute and \(D\) is the dimensionality of the features.

def simulator(x):
    return -np.sum(x**2, axis=1)

The lower and upper bounds of the feature space are specified by min_X and max_X respectively.

min_X = [-2.0, -2.0]
max_X = [2.0, 2.0]

The continuous space version of the Policy class is physbo.search.range.Policy. The constructor takes min_X and max_X as parameters. Also, similar to the discrete space version, you can enable parallel execution by passing mpi4py.MPI.Comm as comm. You can also set the random seed using the set_seed method.

seed = 31415
policy = physbo.search.range.Policy(min_X=min_X, max_X=max_X)
policy.set_seed(seed)

Once the Policy class is created, you can execute optimization following the same flow as the discrete space version. First, to create initial training data for learning the surrogate model, execute random_search.

policy.random_search(max_num_probes=10, simulator=simulator)

0001-th step: f(x) = -0.831185 (action=[0.58327442 0.70069668])
   current best f(x) = -0.831185 (best action=[0.58327442 0.70069668])

0002-th step: f(x) = -5.914186 (action=[1.88281594 1.53921746])
   current best f(x) = -0.831185 (best action=[0.58327442 0.70069668])

0003-th step: f(x) = -4.352756 (action=[1.63626337 1.29437187])
   current best f(x) = -0.831185 (best action=[0.58327442 0.70069668])

0004-th step: f(x) = -0.237057 (action=[-0.05316112  0.48397432])
   current best f(x) = -0.237057 (best action=[-0.05316112  0.48397432])

0005-th step: f(x) = -0.488353 (action=[ 0.57404985 -0.39852174])
   current best f(x) = -0.237057 (best action=[-0.05316112  0.48397432])

0006-th step: f(x) = -2.441356 (action=[1.50087645 0.43442582])
   current best f(x) = -0.237057 (best action=[-0.05316112  0.48397432])

0007-th step: f(x) = -3.440784 (action=[-1.57320004 -0.98276443])
   current best f(x) = -0.237057 (best action=[-0.05316112  0.48397432])

0008-th step: f(x) = -3.452632 (action=[-1.85812001  0.00465691])
   current best f(x) = -0.237057 (best action=[-0.05316112  0.48397432])

0009-th step: f(x) = -0.764532 (action=[ 0.46977882 -0.73745485])
   current best f(x) = -0.237057 (best action=[-0.05316112  0.48397432])

0010-th step: f(x) = -1.850471 (action=[-0.63939092 -1.20068727])
   current best f(x) = -0.237057 (best action=[-0.05316112  0.48397432])

<physbo.search.range._history.History at 0x12a700750>

Next, execute Bayesian optimization with bayes_search.

res = policy.bayes_search(max_num_probes=10, simulator=simulator, score="EI")

Start the initial hyper parameter searching ...
Done

Start the hyper parameter learning ...
0 -th epoch marginal likelihood 14.586042968393608
50 -th epoch marginal likelihood 14.234874815492589
100 -th epoch marginal likelihood 14.063504009485191
150 -th epoch marginal likelihood 13.916750623078872
200 -th epoch marginal likelihood 13.772691286779533
250 -th epoch marginal likelihood 13.633003306706154
300 -th epoch marginal likelihood 13.499200854053448
350 -th epoch marginal likelihood 13.371932369305028
400 -th epoch marginal likelihood 13.251396114620245
450 -th epoch marginal likelihood 13.137551699926508
500 -th epoch marginal likelihood 13.030228562473354
Done

0011-th step: f(x) = -5.026362 (action=[-1.03592362  1.98827161])
   current best f(x) = -0.237057 (best action=[-0.05316112  0.48397432])

0012-th step: f(x) = -0.028634 (action=[0.1327553  0.10492853])
   current best f(x) = -0.028634 (best action=[0.1327553  0.10492853])

0013-th step: f(x) = -0.013414 (action=[0.07031902 0.09202588])
   current best f(x) = -0.013414 (best action=[0.07031902 0.09202588])

0014-th step: f(x) = -0.057856 (action=[0.23418776 0.05488579])
   current best f(x) = -0.013414 (best action=[0.07031902 0.09202588])

0015-th step: f(x) = -0.012249 (action=[ 0.110677   -0.00028234])
   current best f(x) = -0.012249 (best action=[ 0.110677   -0.00028234])

0016-th step: f(x) = -0.015602 (action=[0.12295699 0.02198239])
   current best f(x) = -0.012249 (best action=[ 0.110677   -0.00028234])

0017-th step: f(x) = -0.026756 (action=[0.11124983 0.11991566])
   current best f(x) = -0.012249 (best action=[ 0.110677   -0.00028234])

0018-th step: f(x) = -0.025519 (action=[0.13646757 0.08304057])
   current best f(x) = -0.012249 (best action=[ 0.110677   -0.00028234])

0019-th step: f(x) = -0.005797 (action=[0.07576489 0.00754463])
   current best f(x) = -0.005797 (best action=[0.07576489 0.00754463])

0020-th step: f(x) = -0.032290 (action=[0.09645697 0.15161167])
   current best f(x) = -0.005797 (best action=[0.07576489 0.00754463])

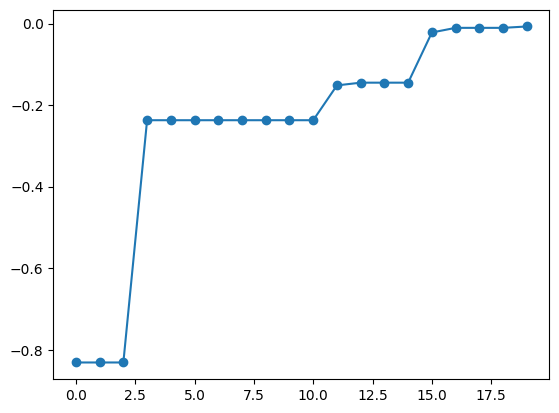
The return value res of the bayes_search function contains the process of Bayesian optimization. Using the export_sequence_best_fx method, you can obtain the optimization results at each step.

best_fx, best_X = res.export_sequence_best_fx()

plt.plot(best_fx, "o-")

[<matplotlib.lines.Line2D at 0x12a4b9390>]

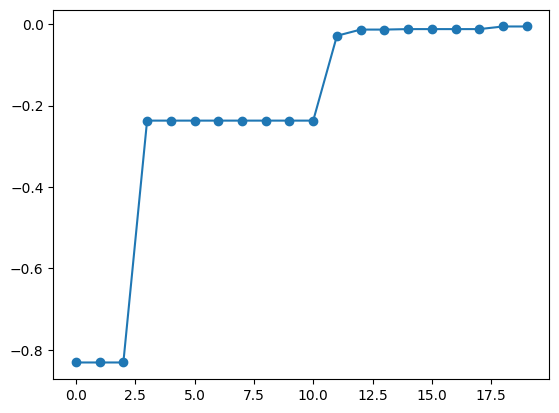
Acquisition Function Optimization Algorithm

For acquisition function optimization, random search is performed by default. This means that nsamples = 1000 candidate points are randomly selected, and the point with the largest acquisition function among them is chosen. To change the value of nsamples, use physbo.search.optimizer.random.Optimizer. For example, if you want to set nsamples = 100, create random_optimizer as follows and pass it to the optimizer keyword of the bayes_search function.

random_optimizer = physbo.search.optimize.random.Optimizer(min_X=min_X, max_X=max_X, nsamples=100)

policy = physbo.search.range.Policy(min_X=min_X, max_X=max_X)
policy.set_seed(seed)
policy.random_search(max_num_probes=10, simulator=simulator)

res = policy.bayes_search(max_num_probes=10, simulator=simulator, score="EI", optimizer=random_optimizer)

best_fx, best_X = res.export_sequence_best_fx()

plt.plot(best_fx, "o-")

0001-th step: f(x) = -0.831185 (action=[0.58327442 0.70069668])
   current best f(x) = -0.831185 (best action=[0.58327442 0.70069668])

0002-th step: f(x) = -5.914186 (action=[1.88281594 1.53921746])
   current best f(x) = -0.831185 (best action=[0.58327442 0.70069668])

0003-th step: f(x) = -4.352756 (action=[1.63626337 1.29437187])
   current best f(x) = -0.831185 (best action=[0.58327442 0.70069668])

0004-th step: f(x) = -0.237057 (action=[-0.05316112  0.48397432])
   current best f(x) = -0.237057 (best action=[-0.05316112  0.48397432])

0005-th step: f(x) = -0.488353 (action=[ 0.57404985 -0.39852174])
   current best f(x) = -0.237057 (best action=[-0.05316112  0.48397432])

0006-th step: f(x) = -2.441356 (action=[1.50087645 0.43442582])
   current best f(x) = -0.237057 (best action=[-0.05316112  0.48397432])

0007-th step: f(x) = -3.440784 (action=[-1.57320004 -0.98276443])
   current best f(x) = -0.237057 (best action=[-0.05316112  0.48397432])

0008-th step: f(x) = -3.452632 (action=[-1.85812001  0.00465691])
   current best f(x) = -0.237057 (best action=[-0.05316112  0.48397432])

0009-th step: f(x) = -0.764532 (action=[ 0.46977882 -0.73745485])
   current best f(x) = -0.237057 (best action=[-0.05316112  0.48397432])

0010-th step: f(x) = -1.850471 (action=[-0.63939092 -1.20068727])
   current best f(x) = -0.237057 (best action=[-0.05316112  0.48397432])

Start the initial hyper parameter searching ...
Done

Start the hyper parameter learning ...
0 -th epoch marginal likelihood 14.586042968393608
50 -th epoch marginal likelihood 14.234874815492589
100 -th epoch marginal likelihood 14.063504009485191
150 -th epoch marginal likelihood 13.916750623078872
200 -th epoch marginal likelihood 13.772691286779533
250 -th epoch marginal likelihood 13.633003306706154
300 -th epoch marginal likelihood 13.499200854053448
350 -th epoch marginal likelihood 13.371932369305028
400 -th epoch marginal likelihood 13.251396114620245
450 -th epoch marginal likelihood 13.137551699926508
500 -th epoch marginal likelihood 13.030228562473354
Done

0011-th step: f(x) = -3.969688 (action=[-0.55371092  1.91392061])
   current best f(x) = -0.237057 (best action=[-0.05316112  0.48397432])

0012-th step: f(x) = -0.048301 (action=[ 0.09981879 -0.19579904])
   current best f(x) = -0.048301 (best action=[ 0.09981879 -0.19579904])

0013-th step: f(x) = -0.026065 (action=[0.00582793 0.16134044])
   current best f(x) = -0.026065 (best action=[0.00582793 0.16134044])

0014-th step: f(x) = -0.029637 (action=[-0.03315978  0.16893146])
   current best f(x) = -0.026065 (best action=[0.00582793 0.16134044])

0015-th step: f(x) = -6.287502 (action=[ 1.84812961 -1.69467382])
   current best f(x) = -0.026065 (best action=[0.00582793 0.16134044])

0016-th step: f(x) = -0.007927 (action=[ 0.06895685 -0.05632176])
   current best f(x) = -0.007927 (best action=[ 0.06895685 -0.05632176])

0017-th step: f(x) = -0.011240 (action=[0.10157691 0.03036993])
   current best f(x) = -0.007927 (best action=[ 0.06895685 -0.05632176])

0018-th step: f(x) = -0.060419 (action=[ 0.1940892  -0.15082425])
   current best f(x) = -0.007927 (best action=[ 0.06895685 -0.05632176])

0019-th step: f(x) = -0.016852 (action=[-0.12738362  0.02501082])
   current best f(x) = -0.007927 (best action=[ 0.06895685 -0.05632176])

0020-th step: f(x) = -0.093609 (action=[0.12668816 0.27849452])
   current best f(x) = -0.007927 (best action=[ 0.06895685 -0.05632176])

[<matplotlib.lines.Line2D at 0x12a8c7290>]

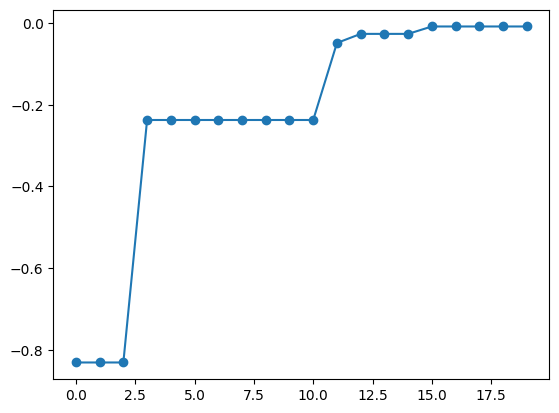
Using optimizers other than physbo.search.optimizer.random.Optimizer, you can utilize maximization algorithms other than random search. PHYSBO provides an optimizer using ODAT-SE: physbo.search.optimize.odatse.Optimizer. This library can solve optimization problems using five algorithms:

• “exchange”: Replica exchange Monte Carlo method

• “pamc”: Population annealing Monte Carlo method

• “minsearch”: Nelder-Mead method

• “mapper”: Grid search

• “bayes”: Bayesian optimization

The algorithms and hyperparameters of ODAT-SE are specified using a dictionary equivalent to the [algorithm] section of the ODAT-SE input file.

The physbo.search.optimize.odatse.default_alg_dict function creates a template for this dictionary, so modify the parameters as needed.

import physbo.search.optimize.odatse
odatse_alg_dict = physbo.search.optimize.odatse.default_alg_dict(min_X=min_X, max_X=max_X, algorithm_name="exchange")

# show the default parameters for the exchange algorithm
odatse_alg_dict

{'name': 'exchange',
 'seed': 12345,
 'param': {'min_list': array([-2., -2.]),
  'max_list': array([2., 2.]),
  'step_list': array([0.04, 0.04])},
 'exchange': {'numsteps': 1000,
  'numsteps_exchange': 10,
  'Tmin': 0.1,
  'Tmax': 10.0,
  'Tlogspace': True,
  'nreplica_per_proc': 10}}

Pass odatse_alg_dict to physbo.search.optimize.odatse.Optimizer to create the optimizer odatse_optimizer. By passing this to the optimizer keyword of the bayes_search function, similar to random_optimizer, you can perform optimization using ODAT-SE.

odatse_optimizer = physbo.search.optimize.odatse.Optimizer(alg_dict=odatse_alg_dict)

policy = physbo.search.range.Policy(min_X=min_X, max_X=max_X)
policy.set_seed(seed)
policy.random_search(max_num_probes=10, simulator=simulator)

res = policy.bayes_search(max_num_probes=10, simulator=simulator, optimizer=odatse_optimizer, score="EI")

0001-th step: f(x) = -0.831185 (action=[0.58327442 0.70069668])
   current best f(x) = -0.831185 (best action=[0.58327442 0.70069668])

0002-th step: f(x) = -5.914186 (action=[1.88281594 1.53921746])
   current best f(x) = -0.831185 (best action=[0.58327442 0.70069668])

0003-th step: f(x) = -4.352756 (action=[1.63626337 1.29437187])
   current best f(x) = -0.831185 (best action=[0.58327442 0.70069668])

0004-th step: f(x) = -0.237057 (action=[-0.05316112  0.48397432])
   current best f(x) = -0.237057 (best action=[-0.05316112  0.48397432])

0005-th step: f(x) = -0.488353 (action=[ 0.57404985 -0.39852174])
   current best f(x) = -0.237057 (best action=[-0.05316112  0.48397432])

0006-th step: f(x) = -2.441356 (action=[1.50087645 0.43442582])
   current best f(x) = -0.237057 (best action=[-0.05316112  0.48397432])

0007-th step: f(x) = -3.440784 (action=[-1.57320004 -0.98276443])
   current best f(x) = -0.237057 (best action=[-0.05316112  0.48397432])

0008-th step: f(x) = -3.452632 (action=[-1.85812001  0.00465691])
   current best f(x) = -0.237057 (best action=[-0.05316112  0.48397432])

0009-th step: f(x) = -0.764532 (action=[ 0.46977882 -0.73745485])
   current best f(x) = -0.237057 (best action=[-0.05316112  0.48397432])

0010-th step: f(x) = -1.850471 (action=[-0.63939092 -1.20068727])
   current best f(x) = -0.237057 (best action=[-0.05316112  0.48397432])

Start the initial hyper parameter searching ...
Done

Start the hyper parameter learning ...
0 -th epoch marginal likelihood 14.586042968393608
50 -th epoch marginal likelihood 14.234874815492589
100 -th epoch marginal likelihood 14.063504009485191
150 -th epoch marginal likelihood 13.916750623078872
200 -th epoch marginal likelihood 13.772691286779533
250 -th epoch marginal likelihood 13.633003306706154
300 -th epoch marginal likelihood 13.499200854053448
350 -th epoch marginal likelihood 13.371932369305028
400 -th epoch marginal likelihood 13.251396114620245
450 -th epoch marginal likelihood 13.137551699926508
500 -th epoch marginal likelihood 13.030228562473354
Done

name            : exchange
seed            : 12345
param.min_list  : [-2. -2.]
param.max_list  : [2. 2.]
param.step_list : [0.04 0.04]
exchange.numsteps: 1000
exchange.numsteps_exchange: 10
exchange.Tmin   : 0.1
exchange.Tmax   : 10.0
exchange.Tlogspace: True
exchange.nreplica_per_proc: 10
complete main process : rank 00000000/00000001
end of run
start separateT 0
Best Result:
  rank = 0
  step = 592
  walker = 7
  fx = -0.08724730012318738
  x1 = -0.6632394188413887
  x2 = 1.2992687470140636
0011-th step: f(x) = -2.127986 (action=[-0.66323942  1.29926875])
   current best f(x) = -0.237057 (best action=[-0.05316112  0.48397432])

name            : exchange
seed            : 12345
param.min_list  : [-2. -2.]
param.max_list  : [2. 2.]
param.step_list : [0.04 0.04]
exchange.numsteps: 1000
exchange.numsteps_exchange: 10
exchange.Tmin   : 0.1
exchange.Tmax   : 10.0
exchange.Tlogspace: True
exchange.nreplica_per_proc: 10
complete main process : rank 00000000/00000001
end of run
start separateT 0
Best Result:
  rank = 0
  step = 3
  walker = 2
  fx = -0.15122627226282423
  x1 = 0.21383031999250043
  x2 = 0.3254993696726256
0012-th step: f(x) = -0.151673 (action=[0.21383032 0.32549937])
   current best f(x) = -0.151673 (best action=[0.21383032 0.32549937])

name            : exchange
seed            : 12345
param.min_list  : [-2. -2.]
param.max_list  : [2. 2.]
param.step_list : [0.04 0.04]
exchange.numsteps: 1000
exchange.numsteps_exchange: 10
exchange.Tmin   : 0.1
exchange.Tmax   : 10.0
exchange.Tlogspace: True
exchange.nreplica_per_proc: 10
complete main process : rank 00000000/00000001
end of run
start separateT 0
Best Result:
  rank = 0
  step = 792
  walker = 4
  fx = -0.045043047258201775
  x1 = 0.2884566379550175
  x2 = 0.24852525678914614
0013-th step: f(x) = -0.144972 (action=[0.28845664 0.24852526])
   current best f(x) = -0.144972 (best action=[0.28845664 0.24852526])

name            : exchange
seed            : 12345
param.min_list  : [-2. -2.]
param.max_list  : [2. 2.]
param.step_list : [0.04 0.04]
exchange.numsteps: 1000
exchange.numsteps_exchange: 10
exchange.Tmin   : 0.1
exchange.Tmax   : 10.0
exchange.Tlogspace: True
exchange.nreplica_per_proc: 10
complete main process : rank 00000000/00000001
end of run
start separateT 0
Best Result:
  rank = 0
  step = 9
  walker = 2
  fx = -0.02392460498257011
  x1 = 0.24246152789117092
  x2 = 0.31119117438511995
0014-th step: f(x) = -0.155628 (action=[0.24246153 0.31119117])
   current best f(x) = -0.144972 (best action=[0.28845664 0.24852526])

name            : exchange
seed            : 12345
param.min_list  : [-2. -2.]
param.max_list  : [2. 2.]
param.step_list : [0.04 0.04]
exchange.numsteps: 1000
exchange.numsteps_exchange: 10
exchange.Tmin   : 0.1
exchange.Tmax   : 10.0
exchange.Tlogspace: True
exchange.nreplica_per_proc: 10
complete main process : rank 00000000/00000001
end of run
start separateT 0
Best Result:
  rank = 0
  step = 9
  walker = 2
  fx = -0.020446511277702712
  x1 = 0.24246152789117092
  x2 = 0.31119117438511995
0015-th step: f(x) = -0.155628 (action=[0.24246153 0.31119117])
   current best f(x) = -0.144972 (best action=[0.28845664 0.24852526])

name            : exchange
seed            : 12345
param.min_list  : [-2. -2.]
param.max_list  : [2. 2.]
param.step_list : [0.04 0.04]
exchange.numsteps: 1000
exchange.numsteps_exchange: 10
exchange.Tmin   : 0.1
exchange.Tmax   : 10.0
exchange.Tlogspace: True
exchange.nreplica_per_proc: 10
complete main process : rank 00000000/00000001
end of run
start separateT 0
Best Result:
  rank = 0
  step = 552
  walker = 2
  fx = -0.07481182997481856
  x1 = 0.13244261916217667
  x2 = 0.06615306139761785
0016-th step: f(x) = -0.021917 (action=[0.13244262 0.06615306])
   current best f(x) = -0.021917 (best action=[0.13244262 0.06615306])

name            : exchange
seed            : 12345
param.min_list  : [-2. -2.]
param.max_list  : [2. 2.]
param.step_list : [0.04 0.04]
exchange.numsteps: 1000
exchange.numsteps_exchange: 10
exchange.Tmin   : 0.1
exchange.Tmax   : 10.0
exchange.Tlogspace: True
exchange.nreplica_per_proc: 10
complete main process : rank 00000000/00000001
end of run
start separateT 0
Best Result:
  rank = 0
  step = 369
  walker = 7
  fx = -0.02747368281669843
  x1 = 0.08963724279512796
  x2 = -0.04990899825183725
0017-th step: f(x) = -0.010526 (action=[ 0.08963724 -0.049909  ])
   current best f(x) = -0.010526 (best action=[ 0.08963724 -0.049909  ])

name            : exchange
seed            : 12345
param.min_list  : [-2. -2.]
param.max_list  : [2. 2.]
param.step_list : [0.04 0.04]
exchange.numsteps: 1000
exchange.numsteps_exchange: 10
exchange.Tmin   : 0.1
exchange.Tmax   : 10.0
exchange.Tlogspace: True
exchange.nreplica_per_proc: 10
complete main process : rank 00000000/00000001
end of run
start separateT 0
Best Result:
  rank = 0
  step = 870
  walker = 3
  fx = -0.025961091903193047
  x1 = 0.14544088137927852
  x2 = 0.043151524528747376
0018-th step: f(x) = -0.023015 (action=[0.14544088 0.04315152])
   current best f(x) = -0.010526 (best action=[ 0.08963724 -0.049909  ])

name            : exchange
seed            : 12345
param.min_list  : [-2. -2.]
param.max_list  : [2. 2.]
param.step_list : [0.04 0.04]
exchange.numsteps: 1000
exchange.numsteps_exchange: 10
exchange.Tmin   : 0.1
exchange.Tmax   : 10.0
exchange.Tlogspace: True
exchange.nreplica_per_proc: 10
complete main process : rank 00000000/00000001
end of run
start separateT 0
Best Result:
  rank = 0
  step = 808
  walker = 1
  fx = -0.009096193960224805
  x1 = -0.1277048769917059
  x2 = -0.01838854551819171
0019-th step: f(x) = -0.016647 (action=[-0.12770488 -0.01838855])
   current best f(x) = -0.010526 (best action=[ 0.08963724 -0.049909  ])

name            : exchange
seed            : 12345
param.min_list  : [-2. -2.]
param.max_list  : [2. 2.]
param.step_list : [0.04 0.04]
exchange.numsteps: 1000
exchange.numsteps_exchange: 10
exchange.Tmin   : 0.1
exchange.Tmax   : 10.0
exchange.Tlogspace: True
exchange.nreplica_per_proc: 10
complete main process : rank 00000000/00000001
end of run
start separateT 0
Best Result:
  rank = 0
  step = 909
  walker = 2
  fx = -0.022643697695937905
  x1 = 0.08090134843314561
  x2 = 0.02494348508299006
0020-th step: f(x) = -0.007167 (action=[0.08090135 0.02494349])
   current best f(x) = -0.007167 (best action=[0.08090135 0.02494349])

best_fx, best_X = res.export_sequence_best_fx()

plt.plot(best_fx, "o-")

[<matplotlib.lines.Line2D at 0x12a8e5c50>]