この jupyter notebook ファイルは ISSP Data Repository (develop branch) から入手できます。

多目的最適化の高速計算

前回のチュートリアルでは、各目的関数を独立にガウス過程回帰し、パレート超体積を直接最大化していました。この方法は、目的関数の数が多い場合に計算時間が膨大になります。

本チュートリアルでは、複数の目的関数を一つの目的関数に統合し、それをベイズ最適化することで、多目的最適化を高速に行う方法を学びます。

多目的最適化の統合

\(i\) 番目のデータ点（特徴量）を \(\vec{x}_i\) とし、その点での目的関数の値を \(\vec{y}_i = (y_{i,1}, y_{i,2}, \dots, y_{i,p})\) とします。 \(\vec{y}_i\) から新たな目的関数 \(z_i\) を作り、 \(\vec{x}_i\) から \(z_i\) への関数 \(z_i = g(\vec{x}_i)\) をガウス過程回帰でモデリングし、ベイズ最適化を行います。

現在の PHYSBO では、 \(\vec{y}_i\) から \(z_i\) を作る方法として、非優越ソート法とParEGO法が提供されています。

非優越ソート法

定義

非優越ソート法 (Non-dominated Sorting; NDS) は、学習データ \(\vec{y}_i\) について非優越ソートによるランク付けを行い、そのランクに基づいた目的関数を新たに作る手法です。ランクは以下のように再帰的に定義されます。

学習データ全体のパレート解となる点のランクは \(r_i = 1\) である。
学習データからランク \(r_i = 1\) となる点を除いた残りのデータのパレート解となる点のランクは \(r_i = 2\) である。
同様に、学習データからランク \(r_i = 1,2,\dots,k-1\) となる点を除いた残りのデータのパレート解となる点のランクは \(r_i = k\) である。
最大ランク \(r_\text{max}\) に達するまで、同様の操作を繰り返す。残った点は \(r_i = \infty\) となる。

ランク \(r_i\) に基づいて、新たな目的関数 \(z_i\) を以下のように定義し、最大化します。

\[z_i = \frac{1}{r_i}\]

PHYSBOでの使い方

PHYSBOでは、 physbo.search.unify.NDS クラスとして NDS 法を実装しています。

unify_method = physbo.search.unify.NDS(rank_max=10)

rank_max はランクの最大値です。これ以上のランクを持つ点については、 \(z_i = 0\) として処理されます。

ParEGO 法

定義

ParEGO法は、目的関数の値について重み付き和と重み付き最大値をとることで、多目的最適化を単目的最適化に帰着させる方法です。目的関数の重みを \(\vec{w} = (w_1, w_2, \dots, w_p)\) とし、和と最大値の重みをそれぞれ \(\rho_\text{sum}\) と \(\rho_\text{max}\) とすると、新たな目的関数は

\[z_i = \rho_\text{sum} \sum_{j} w_j y_{i,j} + \rho_\text{max} \max_{j} w_j y_{i,j}\]

となります。

PHYSBO での使い方

PHYSBOでは、 physbo.search.unify.ParEGO クラスとして ParEGO 法を実装しています。

unify_method = physbo.search.unify.ParEGO(weight_sum=0.05, weight_max=1.0, weights=None, weights_discrete=0)

weight_sum と weight_max はそれぞれ \(\rho_\text{sum}\) と \(\rho_\text{max}\) に対応します。 weights には重み \(\vec{w}\) を指定します。

重み \(\vec{w}\) は \(\sum_{j} w_j = 1\) として自動的に規格化されます。
weights = None とすると、ベイズ最適化のステップごとに重みを乱数で生成します。
- weights_discrete に整数 \(s>0\) を指定すると、それぞれの重みが \(w_j = \frac{a_j}{s}\) となるように生成されます。
  - ここで、 \(a_j\) は \(0, 1, \dots, s\) で、なおかつ \(\sum_{j} a_j = s\) です。
- \(s=0\) の場合は、 \([0,1)\) の範囲で一様ランダムに重みを生成し、和が1になるように規格化されます。

また、 \(y_{i,j}\) は目的関数 \(j\) ごとに、学習データの最小値と最大値を用いて \([-1, 0]\) の範囲に正規化されます。

チュートリアル

前準備

[1]:

import time
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import physbo
%matplotlib inline

seed = 12345
num_random_search = 10
num_bayes_search = 40

テスト関数

本チュートリアルでは引き続き、多目的最適化のベンチマーク関数である VLMOP2 を利用します。なお、PHYSBO では physbo.test_functions.multi_objective に、VLMOP2を含めたいくつかの多目的最適化のベンチマーク関数が用意されています。

[2]:

sim_fn = physbo.test_functions.multi_objective.VLMOP2(dim=2)

探索候補データの準備

sim_fn は探索空間の最小値と最大値を min_X と max_X に持ちます。これらを用いて、 physbo.search.utility.make_grid で探索候補点のグリッドを生成します。

[3]:

test_X = physbo.search.utility.make_grid(min_X=sim_fn.min_X, max_X=sim_fn.max_X, num_X=101)

simulator の定義

[4]:

simu = physbo.search.utility.Simulator(test_X=test_X, test_function=sim_fn)

HVPI

比較対象として、HVPIを用いたベイズ最適化を行います。

[5]:

policy = physbo.search.discrete_multi.Policy(test_X=test_X, num_objectives=2)
policy.set_seed(seed)

policy.random_search(max_num_probes=num_random_search, simulator=simu, is_disp=False)
time_start = time.time()
res_HVPI = policy.bayes_search(max_num_probes=num_bayes_search, simulator=simu, score='HVPI', interval=10, is_disp=False)
time_HVPI = time.time() - time_start
time_HVPI

[5]:

4.317495107650757

[6]:

fig, ax = plt.subplots(figsize=(7, 7))
physbo.search.utility.plot_pareto_front_all(res_HVPI, ax=ax, steps_end=num_random_search, marker="+")
physbo.search.utility.plot_pareto_front_all(res_HVPI, ax=ax, steps_begin=num_random_search)
ax.set_title("HVPI")

[6]:

Text(0.5, 1.0, 'HVPI')

../_images/notebook_tutorial_multi_unified_13_1.png

[7]:

VID_HVPI = res_HVPI.pareto.volume_in_dominance([-1,-1],[0,0])
VID_HVPI

[7]:

np.float64(0.3285497837573861)

ベイズ最適化

Policy クラスは physbo.search.discrete_unified.Policy を利用します。

他の Policy と同じく、 random_search などで初期データを作成し、 bayes_search メソッドでベイズ最適化を行います。他の Policy との違いは以下の通りです。

目的関数の単一化

単一化に使うアルゴリズムは bayes_search の unify_method 引数で指定します。 PHYSBO では physbo.search.unify.ParEGO と physbo.search.unify.NDS が用意されています。

獲得関数

獲得関数は単目的最適化のものと同じです。

PI (Probability of Improvement)
EI (Expected Improvement)
TS (Thompson Sampling)

非優越ソート

[8]:

policy = physbo.search.discrete_unified.Policy(test_X=test_X, num_objectives=2)
policy.set_seed(seed)

unify_method = physbo.search.unify.NDS(num_objectives=2)

policy.random_search(max_num_probes=num_random_search, simulator=simu, is_disp=False)
time_start = time.time()
res_NDS = policy.bayes_search(max_num_probes=num_bayes_search, simulator=simu, unify_method=unify_method, score='EI', interval=10, is_disp=False)
time_NDS = time.time() - time_start
time_NDS

[8]:

1.830704927444458

パレート解のプロット

[9]:

fig, ax = plt.subplots(figsize=(7, 7))
physbo.search.utility.plot_pareto_front_all(res_NDS, ax=ax, steps_end=num_random_search, marker="+")
physbo.search.utility.plot_pareto_front_all(res_NDS, ax=ax, steps_begin=num_random_search)
ax.set_title("NDS")

[9]:

Text(0.5, 1.0, 'NDS')

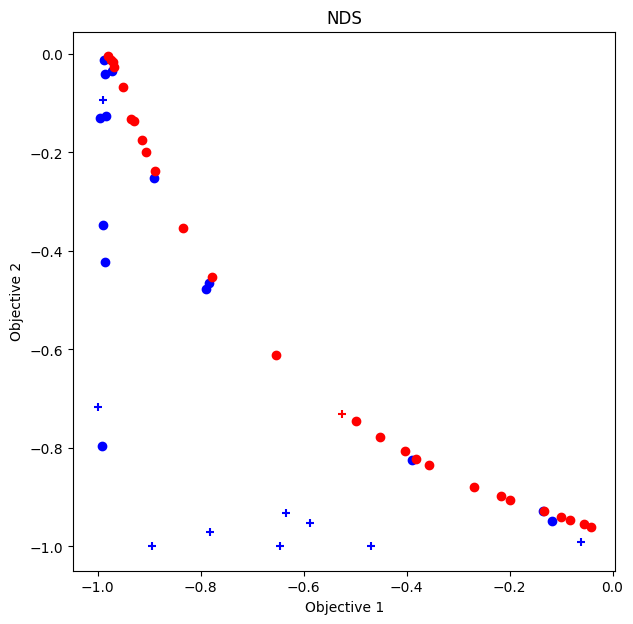
../_images/notebook_tutorial_multi_unified_19_1.png

劣解領域体積

[10]:

VID_NDS = res_NDS.pareto.volume_in_dominance([-1,-1],[0,0])
VID_NDS

[10]:

np.float64(0.30923409715730354)

ParEGO

[11]:

policy = physbo.search.discrete_unified.Policy(test_X=test_X, num_objectives=2)
policy.set_seed(seed)

unify_method = physbo.search.unify.ParEGO(num_objectives=2)

res_random = policy.random_search(max_num_probes=num_random_search, simulator=simu, is_disp=False)
time_start = time.time()
res_ParEGO = policy.bayes_search(max_num_probes=num_bayes_search, simulator=simu, unify_method=unify_method, score='EI', interval=10, is_disp=False)
time_ParEGO = time.time() - time_start
time_ParEGO

[11]:

1.7820510864257812

パレート解のプロット

[12]:

fig, ax = plt.subplots(figsize=(7, 7))
physbo.search.utility.plot_pareto_front_all(res_ParEGO, ax=ax, steps_end=num_random_search, marker="+")
physbo.search.utility.plot_pareto_front_all(res_ParEGO, ax=ax, steps_begin=num_random_search)
ax.set_title("ParEGO")

[12]:

Text(0.5, 1.0, 'ParEGO')

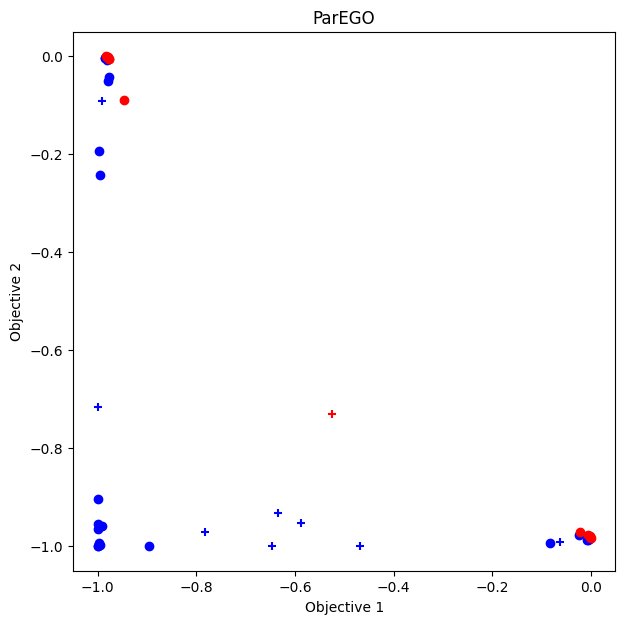
../_images/notebook_tutorial_multi_unified_25_1.png

劣解領域体積

[13]:

VID_ParEGO = res_ParEGO.pareto.volume_in_dominance([-1,-1],[0,0])
VID_ParEGO

[13]:

np.float64(0.18004551161609372)

比較

[14]:

# make table
df = pd.DataFrame({
    "アルゴリズム": ["NDS", "ParEGO", "HVPI"],
    "計算時間": [time_NDS, time_ParEGO, time_HVPI],
    "劣解領域体積": [VID_NDS, VID_ParEGO, VID_HVPI]
})
df

[14]:

	アルゴリズム	計算時間	劣解領域体積
0	NDS	1.830705	0.309234
1	ParEGO	1.782051	0.180046
2	HVPI	4.317495	0.328550

NDS は HVPI と比較しても遜色ない結果（劣解領域体積）を、より短い計算時間で得ることができています。

一方のParEGOは、計算時間こそ短いですが、劣解領域体積が小さくなっています。

最適化問題によって、どのアルゴリズムがよい結果を出すかは変わります。

別のベンチマーク関数

Kita-Yabumoto-Mori-Nishikawa 関数を用いたベイズ最適化を行います。

\[\begin{split}\begin{cases} f_1(x, y) = -x^2 + y^2 \\ f_2(x, y) = 0.5x + y + 1 \\ \end{cases}\end{split}\]

の2つの目的関数を最大化する問題です。

また、 \(x\) と \(y\) には

\[\begin{split}\begin{cases} g_1(x, y) = 6.5 - x/6 - y \ge 0 \\ g_2(x, y) = 7.5 - x/2 - y \ge 0 \\ g_3(x, y) = 30 - 5x - y \ge 0 \\ \end{cases}\end{split}\]

という制約条件があります。

Kita, H., Yabumoto, Y., Mori, N., Nishikawa, Y. (1996). Multi-objective optimization by means of the thermodynamical genetic algorithm. In: Voigt, HM., Ebeling, W., Rechenberg, I., Schwefel, HP. (eds) Parallel Problem Solving from Nature — PPSN IV. PPSN 1996. Lecture Notes in Computer Science, vol 1141. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-61723-X_1014

[15]:

fn_KYMN = physbo.test_functions.multi_objective.KitaYabumotoMoriNishikawa()
test_X_KYMN = physbo.search.utility.make_grid(min_X=fn_KYMN.min_X, max_X=fn_KYMN.max_X, num_X=101, constraint=fn_KYMN.constraint)
simu_KYMN = physbo.search.utility.Simulator(test_X=test_X_KYMN, test_function=fn_KYMN)

HVPI

[16]:

policy = physbo.search.discrete_multi.Policy(test_X=test_X_KYMN, num_objectives=2)
policy.set_seed(seed)

policy.random_search(max_num_probes=num_random_search, simulator=simu_KYMN, is_disp=False)
time_start = time.time()
res_KYMN_HVPI = policy.bayes_search(max_num_probes=num_bayes_search, simulator=simu_KYMN, score='HVPI', interval=10, is_disp=False)
time_KYMN_HVPI = time.time() - time_start
VID_KYMN_HVPI = res_KYMN_HVPI.pareto.volume_in_dominance(fn_KYMN.reference_min, fn_KYMN.reference_max)
VID_KYMN_HVPI
fig, ax = plt.subplots(figsize=(7, 7))
physbo.search.utility.plot_pareto_front_all(res_KYMN_HVPI, ax=ax, steps_end=num_random_search, marker="+")
physbo.search.utility.plot_pareto_front_all(res_KYMN_HVPI, ax=ax, steps_begin=num_random_search)
ax.set_xlim(-60, 10)
ax.set_ylim(-10, 8)
ax.set_title("HVPI")

[16]:

Text(0.5, 1.0, 'HVPI')

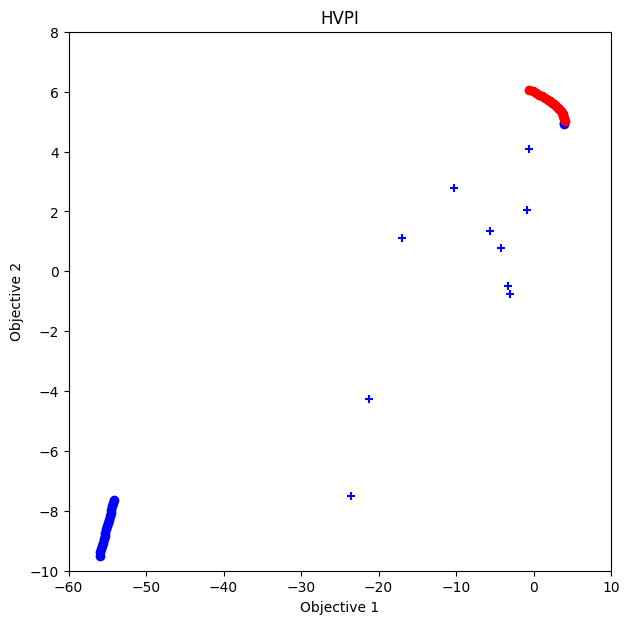
../_images/notebook_tutorial_multi_unified_34_1.png

ParEGO

[17]:

policy = physbo.search.discrete_unified.Policy(test_X=test_X_KYMN, num_objectives=2)
policy.set_seed(seed)

unify_method = physbo.search.unify.ParEGO(num_objectives=2)

policy.random_search(max_num_probes=num_random_search, simulator=simu_KYMN, is_disp=False)
time_start = time.time()
res_KYMN_ParEGO = policy.bayes_search(max_num_probes=num_bayes_search, simulator=simu_KYMN, unify_method=unify_method, score='EI', interval=10, is_disp=False)
time_KYMN_ParEGO = time.time() - time_start
VID_KYMN_ParEGO = res_KYMN_ParEGO.pareto.volume_in_dominance(fn_KYMN.reference_min, fn_KYMN.reference_max)
VID_KYMN_ParEGO
fig, ax = plt.subplots(figsize=(7, 7))
physbo.search.utility.plot_pareto_front_all(res_KYMN_ParEGO, ax=ax, steps_end=num_random_search, marker="+")
physbo.search.utility.plot_pareto_front_all(res_KYMN_ParEGO, ax=ax, steps_begin=num_random_search)
ax.set_xlim(-60, 10)
ax.set_ylim(-10, 8)
ax.set_title("ParEGO")

[17]:

Text(0.5, 1.0, 'ParEGO')

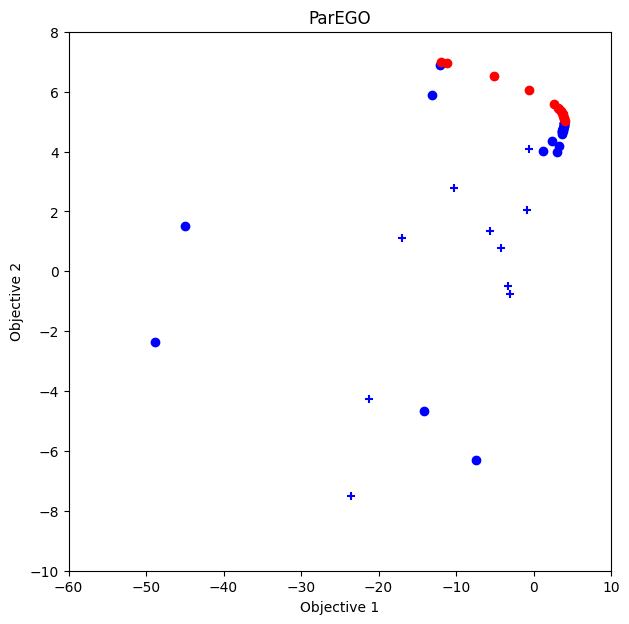
../_images/notebook_tutorial_multi_unified_36_1.png

NDS

[18]:

policy = physbo.search.discrete_unified.Policy(test_X=test_X_KYMN, num_objectives=2)
policy.set_seed(seed)

unify_method = physbo.search.unify.NDS(num_objectives=2)

policy.random_search(max_num_probes=num_random_search, simulator=simu_KYMN, is_disp=False)
time_start = time.time()
res_KYMN_NDS = policy.bayes_search(max_num_probes=num_bayes_search, simulator=simu_KYMN, unify_method=unify_method, score='EI', interval=10, is_disp=False)
time_KYMN_NDS = time.time() - time_start
VID_KYMN_NDS = res_KYMN_NDS.pareto.volume_in_dominance(fn_KYMN.reference_min, fn_KYMN.reference_max)
VID_KYMN_NDS
fig, ax = plt.subplots(figsize=(7, 7))
physbo.search.utility.plot_pareto_front_all(res_KYMN_NDS, ax=ax, steps_end=num_random_search, marker="+")
physbo.search.utility.plot_pareto_front_all(res_KYMN_NDS, ax=ax, steps_begin=num_random_search)
ax.set_xlim(-60, 10)
ax.set_ylim(-10, 8)
ax.set_title("NDS")

[18]:

Text(0.5, 1.0, 'NDS')

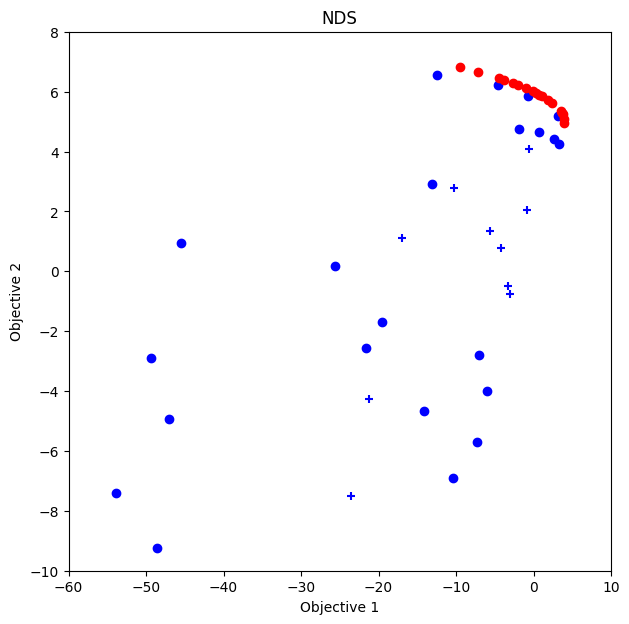
../_images/notebook_tutorial_multi_unified_38_1.png

比較

[19]:

pd.DataFrame({
    "アルゴリズム": ["NDS", "ParEGO", "HVPI"],
    "計算時間": [time_KYMN_NDS, time_KYMN_ParEGO, time_KYMN_HVPI],
    "劣解領域体積": [VID_KYMN_NDS, VID_KYMN_ParEGO, VID_KYMN_HVPI]
})

[19]:

	アルゴリズム	計算時間	劣解領域体積
0	NDS	1.769309	970.781427
1	ParEGO	1.763690	975.909589
2	HVPI	3.961754	932.139351

この最適化問題では、 ParEGOがよい結果を出しています。