5.2. tenes_simple の入力ファイル

  • ファイルフォーマットは TOML 形式

  • model, lattice, parameter, correlation の4つのセクションを持ちます。

    • parameter セクションはそのままスタンダードモードの入力へとコピーされます。

5.2.1. model セクション

計算する模型を指定します。 スピン系 (spin) および ボソン系 (boson) が定義済みです。

名前

説明

型

デフォルト

type

模型の種類 ("spin" もしくは "boson")

文字列

--

模型の種類によって相互作用などのパラメータ名が変わります。

スピン系 spin

スピン系

\[\mathcal{H} = \sum_{i < j}\left[\sum_\alpha^{x,y,z} J^\alpha_{ij} S^\alpha_i S^\alpha_j + B_{ij} \left(\vec{S}_i\cdot\vec{S}_j\right)^2 \right] - \sum_i \sum_\alpha^{x,y,z} h^\alpha S^\alpha_i - D \sum_i \left(S^z_i\right)^2\]

一体項のパラメータは次の通り。

名前

説明

型

デフォルト

S

局所スピンの大きさ

実数（整数もしくは半整数）

0.5

hx

\(S^x\) 方向の磁場 \(h^x\)

実数

0.0

hy

\(S^y\) 方向の磁場 \(h^y\)

実数

0.0

hz

\(S^z\) 方向の磁場 \(h^z\)

実数

0.0

D

オンサイトスピン異方性 D

実数

0.0

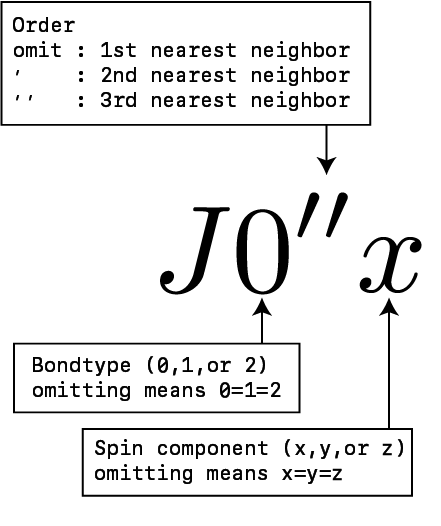
交換相互作用 \(J\) にはボンド依存性をもたせることができます。

名前

説明

型

デフォルト

J0

最近接・第0方向ボンドの交換相互作用

実数

0.0

J1

最近接・第1方向ボンドの交換相互作用

実数

0.0

J2

最近接・第2方向ボンドの交換相互作用

実数

0.0

J0'

次近接・第0方向ボンドの交換相互作用

実数

0.0

J1'

次近接・第1方向ボンドの交換相互作用

実数

0.0

J2'

次近接・第2方向ボンドの交換相互作用

実数

0.0

J0''

三次近接・第0方向ボンドの交換相互作用

実数

0.0

J1''

三次近接・第1方向ボンドの交換相互作用

実数

0.0

J2''

三次近接・第2方向ボンドの交換相互作用

実数

0.0

次近接、三次近接相互作用を与える場合には、名前をダブルクォーテーションマーク " で囲んでください。 ボンドの方向は lattice セクションで定義される格子に依存します。 例えば正方格子では x方向 (0) と y方向 (1) の2種類のボンド方向ごとに定義できます。 方向を示す番号を省略することで、すべての方向について一度に指定できます。 また、最後に xyz のうち一文字を追加するとイジング的な相互作用を指定できます。 同一ボンド・同一成分を2回以上指定するとエラー終了します。

../_images/J.png

双二次相互作用 \(B\) も \(J\) と同様にボンド依存性をもたせられます。

名前

説明

型

デフォルト

B0

最近接・第0方向ボンドの双二次相互作用

実数

0.0

B1

最近接・第1方向ボンドの双二次相互作用

実数

0.0

B2

最近接・第2方向ボンドの双二次相互作用

実数

0.0

B0'

次近接・第0方向ボンドの双二次相互作用

実数

0.0

B1'

次近接・第1方向ボンドの双二次相互作用

実数

0.0

B2'

次近接・第2方向ボンドの双二次相互作用

実数

0.0

B0''

三次近接・第0方向ボンドの双二次相互作用

実数

0.0

B1''

三次近接・第1方向ボンドの双二次相互作用

実数

0.0

B2''

三次近接・第2方向ボンドの双二次相互作用

実数

0.0

物理量測定に使われる1サイト物理量として、 \(S^z\) と \(S^x\) 、(parameter.general.is_real = false ならば) \(S^y\) が自動的に定義されます。 また、2サイト物理量として、ボンドハミルトニアン

\[\mathcal{H}_{ij} = \left[\sum_\alpha^{x,y,z} J^\alpha_{ij} S^\alpha_i S^\alpha_j + B_{ij} \left(\vec{S}_i\cdot\vec{S}_j\right)^2 \right] - \frac{1}{z} \left[ \sum_\alpha^{x,y,z} h^\alpha \left(S^\alpha_i + S^\alpha_j \right) + D \left(\left(S^z_i\right)^2 + \left(S^z_j\right)^2 \right) \right],\]

および最近接ボンド上の相関 \(S_i^\alpha S_j^\alpha\) ( \(\alpha=x, y, z\) )が自動的に定義されます。 ここで、ボンドハミルトニアンのうち、 \(z\) はひとつのサイトから伸びる最近接ボンドの本数で、また一体項の寄与は最近接ボンドにのみ定義されます。

ボソン系 boson

ボソン系

\[\mathcal{H} = \sum_{i<j}\left[ -t_{ij} \left(b^\dagger_i b_j + b^\dagger_j b_i \right) + V_{ij} n_i n_j \right] + \sum_i \left[U\frac{n_i(n_i-1)}{2} - \mu n_i\right]\]

ここで \(b\) と \(b^\dagger\) はボース粒子の生成消滅演算子で、 \(n = b^\dagger b\) は数演算子。

一体項のパラメータは次の通り。

名前

説明

型

デフォルト

nmax

1サイトに入る粒子の最大数

整数

1

U

オンサイト斥力

実数

0.0

mu

化学ポテンシャル

実数

0.0

ホッピング \(t\) およびオフサイト斥力 \(V\) にはボンド依存性をもたせることができます。

名前

説明

型

デフォルト

t0

最近接・第0方向ボンドのホッピング

実数

0.0

t1

最近接・第1方向ボンドのホッピング

実数

0.0

t2

最近接・第2方向ボンドのホッピング

実数

0.0

t0'

次近接・第0方向ボンドのホッピング

実数

0.0

t1'

次近接・第1方向ボンドのホッピング

実数

0.0

t2'

次近接・第2方向ボンドのホッピング

実数

0.0

t0''

三次近接・第0方向ボンドのホッピング

実数

0.0

t1''

三次近接・第1方向ボンドのホッピング

実数

0.0

t2''

三次近接・第2方向ボンドのホッピング

実数

0.0

V0

最近接・第0方向ボンドのオフサイト斥力

実数

0.0

V1

最近接・第1方向ボンドのオフサイト斥力

実数

0.0

V2

最近接・第2方向ボンドのオフサイト斥力

実数

0.0

V0'

次近接・第0方向ボンドのオフサイト斥力

実数

0.0

V1'

次近接・第1方向ボンドのオフサイト斥力

実数

0.0

V2'

次近接・第2方向ボンドのオフサイト斥力

実数

0.0

V0''

三次近接・第0方向ボンドのオフサイト斥力

実数

0.0

V1''

三次近接・第1方向ボンドのオフサイト斥力

実数

0.0

V2''

三次近接・第2方向ボンドのオフサイト斥力

実数

0.0

ボンドの方向は lattice セクションで定義される格子に依存します。 例えば正方格子では x方向 (0) と y方向 (1) の2種類のボンド方向ごとに定義できます。 方向を示す番号を省略することで、すべての方向について一度に指定できます。

物理量測定に使われる1サイト物理量として、 \(n\) と \(b\), \(b^\dagger\) が自動的に定義されます。 また、2サイト物理量として、ボンドハミルトニアン

\[\mathcal{H}_{ij} = \left[ -t_{ij} \left(b^\dagger_i b_j + b^\dagger_j b_i \right) + V_{ij} n_i n_j \right] + \frac{1}{z} \left[\left(U\frac{n_i(n_i-1)}{2} - \mu n_i\right) + (i \leftrightarrow j)\right]\]

および最近接ボンド上の相関 \(n_i n_j\), \(b^\dagger_i b\), \(b_i b^\dagger_j\) が自動的に定義されます。 ここで、ボンドハミルトニアンのうち、 \(z\) はひとつのサイトから伸びる最近接ボンドの本数で、また一体項の寄与は最近接ボンドにのみ定義されます。

5.2.2. lattice セクション

計算する格子を指定します。 正方格子 (square) と 三角格子 (triangular), 蜂の巣格子 (honeycomb) , かごめ格子 (kagome) が定義されています。 TeNeS では波動関数を正方格子状に並べられたテンソルによるテンソル積状態で表現し、計算を行います。 そのため、これらの格子（物理格子）と、計算される正方格子との対応についても記述します。

名前

説明

型

デフォルト

type

格子名 (square, triangular, honeycomb, もしくは kagome)

文字列

--

L

ユニットセルのx 方向の大きさ

整数

--

W

ユニットセルのy 方向の大きさ

整数

L

virtural_dim

ボンド次元

整数

--

initial

初期状態

文字列

random

noise

初期テンソルの揺らぎ

実数

1e-2

initial と noise は波動関数の初期状態を決めるパラメータです。 なお、 parameter.general で tensor_load が設定されている場合には、そちらが優先され、テンソルをファイルから読み込みます。

  • initial

    • "ferro" : 強磁性状態。

      • スピン系では、各サイトで \(S^z=S`\) となる状態。

      • ボソン系では、各サイトで \(n=n_{\text{max}}`\) となる状態。

    • "antiferro" : 反強磁性状態。

      • スピン系では、 正方格子、蜂の巣格子で \(S^z = S\) と \(S^z = -S\) が互いに並んだNeel 秩序。 三角格子、かごめ格子で スピンが \((\theta, \phi) = (0, 0), (2\pi/3, 0), (2\pi/3, \pi)\) 方向に向いた120 度秩序。

      • ボソン系では、一つの副格子で \(n=n_{\text{max}}\) となり、他の副格子では \(n=0\) となる状態。

    • "random" : 各サイトバラバラなランダム状態。

  • noise

    • テンソルの要素に付与されるゆらぎの大きさ。

正方格子 square lattice

正方格子 type = "square lattice" では、 サイトが \((1,0)\) 方向に L 個、 \((0,1)\) 方向に W 個並びます。 具体例として、 L=3, W=3 のときのサイトの並びを 図 5.1 (a) に示します。 また、最近接、次近接、三次近接のボンドタイプの定義を 図 5.1 (b), (c), (d) にそれぞれ示します。 青線は bondtype = 0 のボンドを, 赤線は bondtype = 1 のボンドを表します。

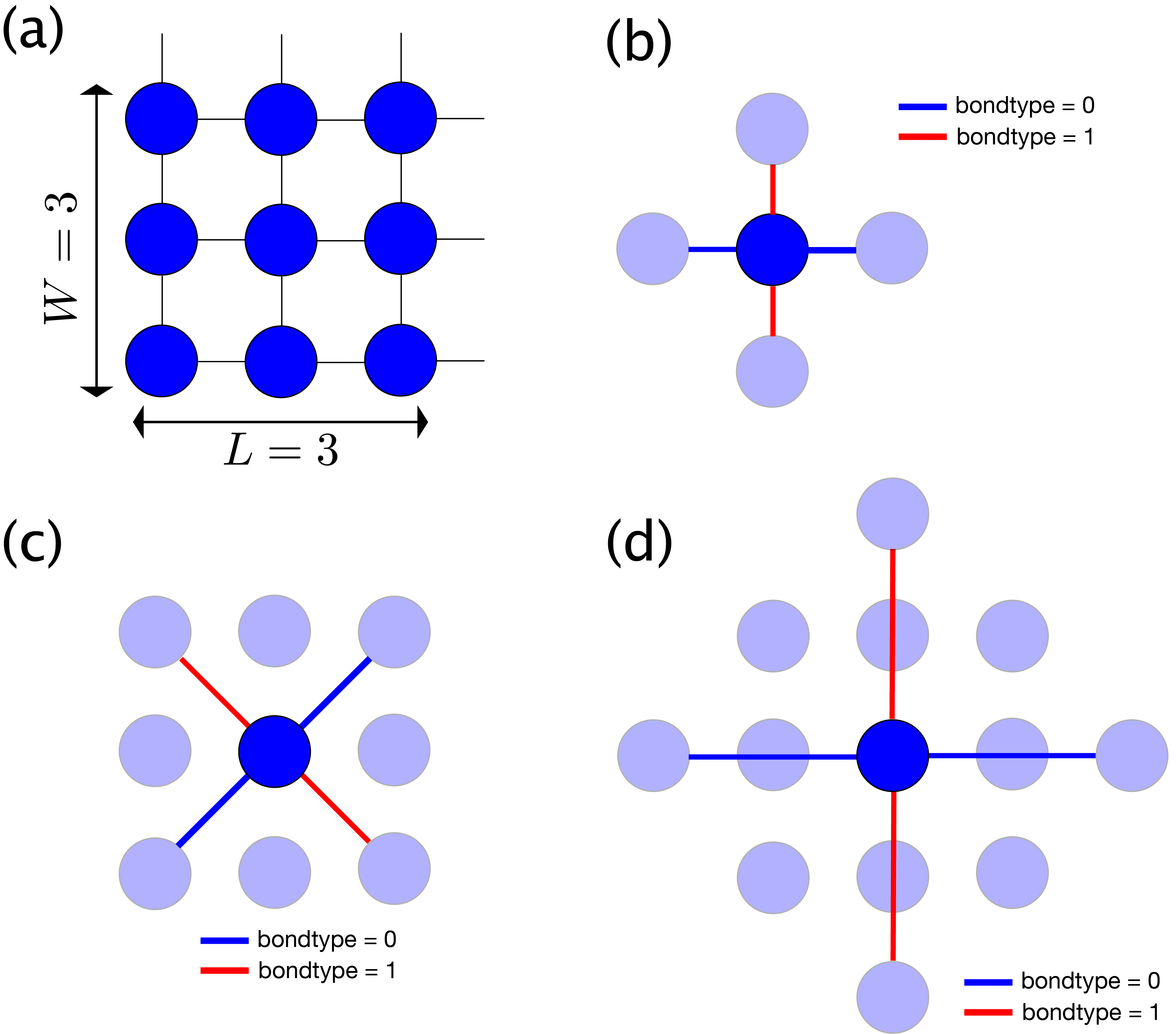
../_images/SquareLattice.png

図 5.1 正方格子 (square) のサイト・ボンド。 (a) L=3, W=3 としたときのサイトの並び。 (b) 最近接ボンド。 bondtype=0 (青) は 0 度方向に、 bondtype=1 (赤) は 90度方向に伸びる。 (c) 次近接ボンド。 bondtype=0 (青) は 45 度方向に、 bondtype=1 (赤) は -45度方向に伸びる。 (d) 三次近接ボンド。 bondtype=0 (青) は 0 度方向に、 bondtype=1 (赤) は 90度方向に伸びる。

三角格子 triangular lattice

三角格子 type = "triangular lattice" では、 サイトが \((1,0)\) 方向に L 個、 \((1/2, \sqrt{3}/2)\) 方向に W 個並びます。 具体例として、 L=3, W=3 のときのサイトの並びを 図 5.2 (a) に示します。 また、最近接、次近接、三次近接のボンドタイプの定義を 図 5.2 (b), (c), (d) にそれぞれ示します。 青線は bondtype = 0 のボンドを、 赤線は bondtype = 1 のボンドを、 緑線は bondtype = 2 のボンドを、それぞれ表します。 図 5.2 (e) 図は (a) に等価な正方格子をあらわしています。

../_images/TriangularLattice.png

図 5.2 三角格子 (triangular) のサイト・ボンド。 (a) L=3, W=3 としたときのサイトの並び。 (b) 最近接ボンド。 bondtype=0 (青) は 0 度方向に、 bondtype=1 (赤) は 60度方向に、 bondtype=2 (緑)は 120度方向にそれぞれ伸びる。 (c) 次近接ボンド。 bondtype=0 (青) は 90 度方向に、 bondtype=1 (赤) は -30度方向に、 bondtype=2 (緑)は 30度方向にそれぞれ伸びる。 (d) 三次近接ボンド。 bondtype=0 (青) は 0 度方向に、 bondtype=1 (赤) は 60度方向に、 bondtype=2 (緑)は 120度方向にそれぞれ伸びる。 (e) 正方格子テンソル積状態との対応。

蜂の巣格子 honeycomb lattice

蜂の巣格子 type = "honeycomb lattice" では、 座標 \((0, 0)\) と \((\sqrt{3}/2, 1/2)\) の2つのサイトからなるユニットが、 \((\sqrt{3},0)\) 方向に L 個、 \((1/2, 3/2)\) 方向に W 個並びます。 具体例として、L=2, W=2 のときのサイトの並びを 図 5.3 (a) に示します。 破線はユニットを表します。 また、最近接、次近接、三次近接のボンドタイプの定義を 図 5.3 (b), (c), (d) にそれぞれ示します。 青線は bondtype = 0 のボンドを、 赤線は bondtype = 1 のボンドを、 緑線は bondtype = 2 のボンドを、それぞれ表します。 図 5.3 (e) 図は (a) に等価な正方格子をあらわしています。 青サイトから上に伸びるボンドなど、正方格子にはあるものの蜂の巣格子には存在しないものは、ボンド次元が 1 のボンドとして表現されます。

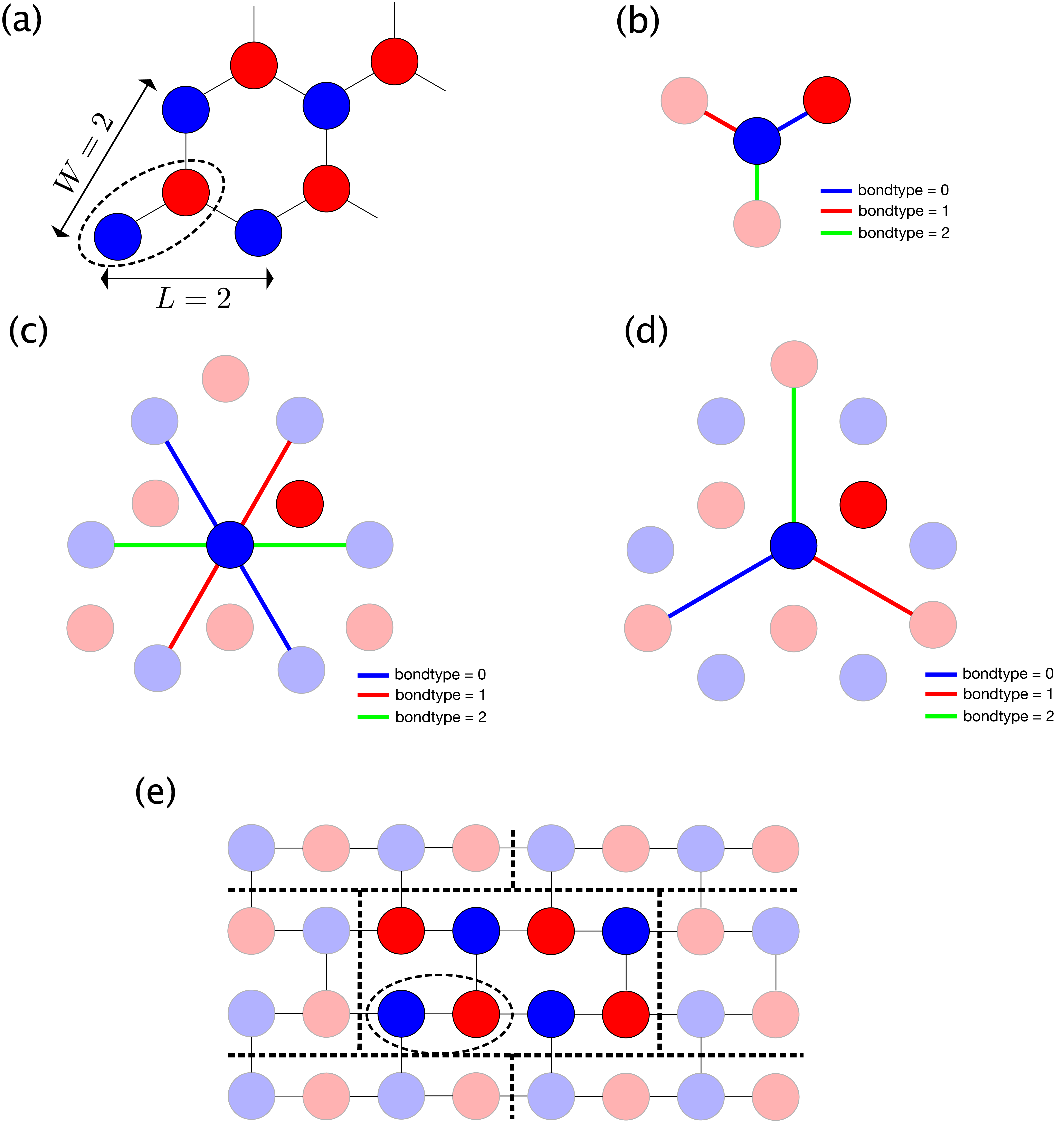
../_images/HoneycombLattice.png

図 5.3 蜂の巣格子 (honeycomb) のサイト・ボンド。 (a) L=2, W=2 としたときのサイトの並び。 破線で表されるユニットが L かける W 個並ぶ。 (b) 最近接ボンド。 bondtype=0 (青) は 30 度方向に、 bondtype=1 (赤) は 150度方向に、 bondtype=2 (緑)は -90度方向にそれぞれ伸びる。 (c) 次近接ボンド。 bondtype=0 (青) は 120 度方向に、 bondtype=1 (赤) は 60度方向に、 bondtype=2 (緑)は 0度方向にそれぞれ伸びる。 (d) 三次近接ボンド。 bondtype=0 (青) は -30 度方向に、 bondtype=1 (赤) は -150度方向に、 bondtype=2 (緑)は 90度方向にそれぞれ伸びる。 (e) 正方格子テンソル積状態との対応。大きな破線はユニットセルの境界を表し、周りにある薄いユニットセルは中心にあるユニットセルのコピーである。 ユニットセルの並びが少しずれていること、また、 (a) で一番右上にあった赤いサイトが (e) では等価な左上に移動することに注意。

かごめ格子 kagome lattice

かごめ格子 type = "kagome lattice" では、 座標 \((0, 0)\), \((1, 0)\), \((1/2, \sqrt{3}/2)\) の3つのサイトからなるユニット（上向き三角）が、 \((2,0)\) 方向に L 個、 \((1, \sqrt{3})\) 方向に W 個並びます。 具体例として、L=2, W=2 のときのサイトの並びを 図 5.4 (a) に示します。 破線はユニットは破線を表します。 また、最近接、次近接、三次近接のボンドタイプの定義を 図 5.4 (b), (c), (d) にそれぞれ示します。 青線は bondtype = 0 のボンドを、 赤線は bondtype = 1 のボンドを表します。

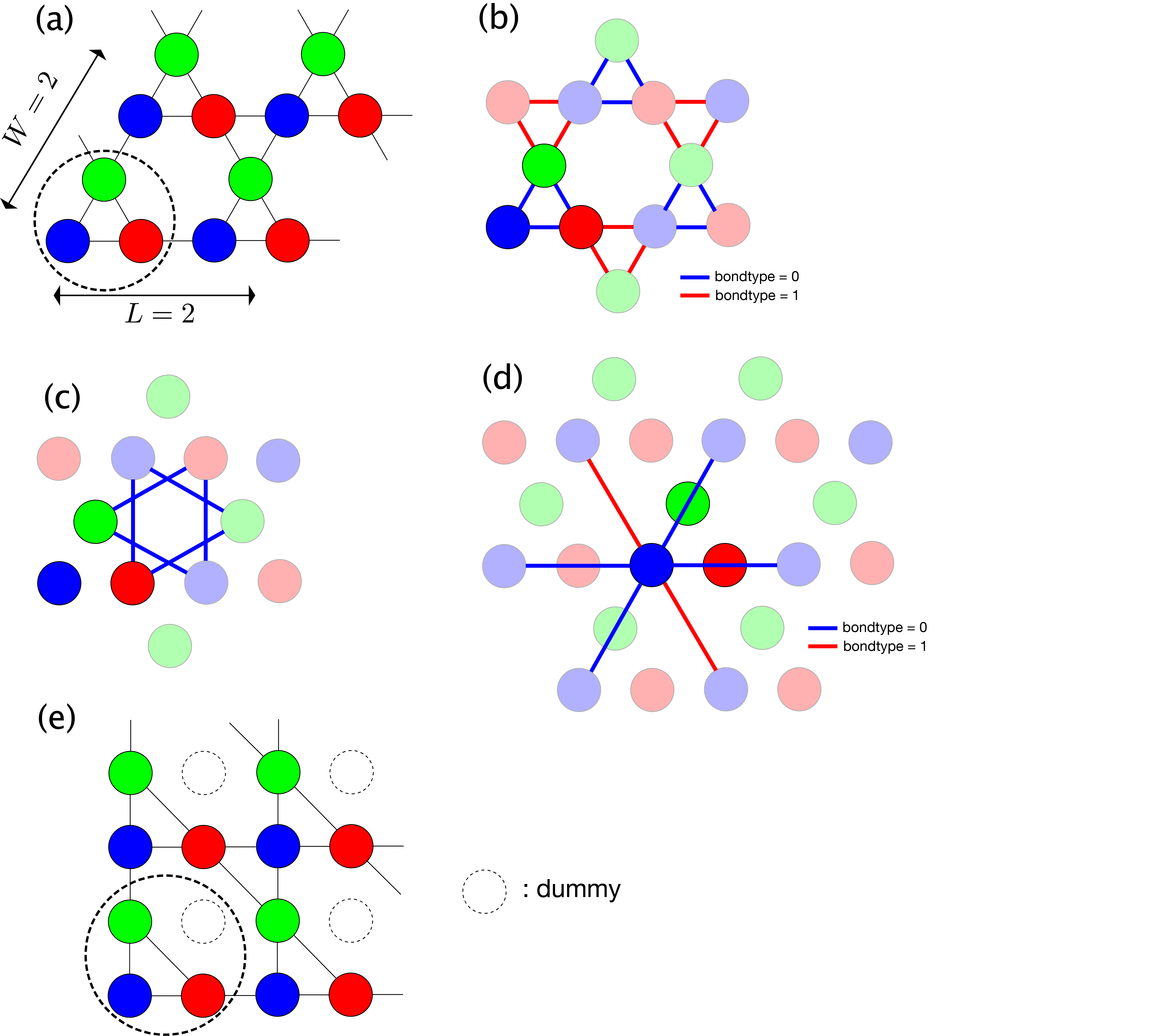
../_images/KagomeLattice.png

図 5.4 かごめ格子 (kagome) のサイト・ボンド。 (a) L=2, W=2 としたときのサイトの並び。 破線で表されるユニットが L かける W 個並ぶ。 (b) 最近接ボンド。 bondtype=0 (青) は 上向き三角形を、 bondtype=1 (赤) は 下向き三角形を作る。 (c) 次近接ボンド。 (d) 三次近接ボンド。 bondtype=0 (青) はサイトを横切り、 bondtype=1 (赤) は横切らない。 (e) 正方格子テンソル積状態との対応。点線で描かれた白丸はすべての次元が1のダミーサイト。

5.2.3. parameter セクション

tenes_simple では使われず、 tenes_std の入力ファイルとしてそのままコピーされます。

更新回数など、 計算にあらわれる種々のパラメータを記述します。 サブセクションとして general, simple_update, full_update, ctm, random を持ちます。

parameter.general

tenes の全般的な設定パラメータ

名前

説明

型

デフォルト

mode

計算モード

文字列

"ground state"

is_real

すべてのテンソルを実数に制限するかどうか

真偽値

false

iszero_tol

演算子テンソルの読み込みにおいてゼロとみなす絶対値カットオフ

実数

0.0

measure

基底状態計算において、物理量測定をするかどうか

真偽値

true

measure_interval

実時間発展・有限温度計算において物理量を測定する頻度

整数 or 整数のリスト

10

output

物理量などを書き込むディレクトリ

文字列

"output"

tensor_save

最適化後のテンソルを書き込むディレクトリ

文字列

""

tensor_load

初期テンソルを読み込むディレクトリ

文字列

""

  • mode

    • 計算モードを指定します

    • "ground state"

      • 基底状態計算

      • tenes_std は虚時間発展演算子 \(U(\tau) = \exp(-\tau \mathcal{H})\) を計算します

    • "time evolution"

      • 実時間発展計算

      • tenes_std は実時間発展演算子 \(U(t) = \exp(-it \mathcal{H})\) を計算します

    • "finite temperature"

      • 有限温度計算

      • tenes_std は虚時間発展演算子 \(U(\tau) = \exp(-\tau \mathcal{H})\) を計算します

  • is_real

    • true にするとテンソルの要素を実数に制限して計算を行います

    • 一つでも複素演算子があるとエラー終了します

  • iszero_tol

    • 各種演算子テンソル要素の実部・虚部の読み込みにおいて、絶対値が iszero_tol 以下はゼロとみなします

  • measure

    • 基底状態計算において、 false にすると物理量計算・保存をスキップします

    • 実行時間 time.dat は常に保存されます

  • measure_interval

    • 実時間発展計算および有限温度計算において、 物理量を測定する頻度を指定します

    • measure_interval ステップ計算した後に物理量を測定します

  • output

    • 物理量などの計算結果をこのディレクトリ以下に保存します

    • 空文字列の場合はカレントディレクトリに保存します

  • tensor_save

    • 最適化後のテンソルをこのディレクトリ以下に保存します

    • 空文字列の場合は保存しません

  • tensor_load

    • 初期テンソルをこのディレクトリ以下から読み込みます

    • 空文字列の場合は読み込みません

parameter.simple_update

simple update に関するパラメータ

名前

説明

型

デフォルト

tau

(虚)時間発展演算子における(虚)時間刻み \(\tau\)

実数 or 実数のリスト

0.01

num_step

simple update の回数

整数 or 整数のリスト

0

lambda_cutoff

simple update において平均場 \(\lambda\) の切り捨て閾値

実数

1e-12

gauge_fix

テンソルのゲージを固定するかどうか

真偽値

false

gauge_maxiter

ゲージ固定操作のループ最大数

整数

100

gauge_convergence_epsilon

ゲージ固定操作の収束判定値

実数

1e-2

  • tau

    • (虚)時間発展演算子における(虚)時間刻み \(\tau\) を指定します

      • tenes_std では時間発展演算子を計算するために用いられます

      • tenes では各ステップでの経過時間・逆温度を求めるために用いられます

        • For finite temperature calculation, note that the inverse temperature increase \(2\tau\) at a step because \(\rho(\beta + 2\tau) = U(\tau)\rho(\beta)\bar{U}(\tau)\)

        • 有限温度計算の場合、 \(\rho(\beta + 2\tau) = U(\tau)\rho(\beta)\bar{U}(\tau)\) なので、 ステップごとに逆温度は \(2\tau\) だけ増加することに注意してください。

    • リストを指定すると、時間発展演算子のグループごとに刻み幅を変えることができます

  • num_step

    • simple update の回数を指定します

    • リストを指定すると、時間発展演算子のグループごとに回数を変えることができます

parameter.full_update

full update に関するパラメータ

名前

説明

型

デフォルト

tau

(虚)時間発展演算子における(虚)時間刻み \(\tau\)

実数 or 実数のリスト

0.01

num_step

full update の回数

整数 or 整数のリスト

0

env_cutoff

full update で環境テンソルを計算する際にゼロとみなす特異値のcutoff

実数

1e-12

inverse_precision

full update で擬似逆行列を計算する際にゼロとみなす特異値のcutoff

実数

1e-12

convergence_epsilon

full update でtruncationの最適化を行う際の収束判定値

実数

1e-6

iteration_max

full update でtruncationの最適化を行う際のiterationの最大回数

整数

100

gauge_fix

テンソルのゲージを固定するかどうか

真偽値

true

fastfullupdate

Fast full update にするかどうか

真偽値

true

parameter.ctm

角転送行列 (CTM) に関するパラメータ

名前

説明

型

デフォルト

dimension

CTM のボンド次元 \(\chi\)

整数

4

projector_cutoff

CTMのprojectorを計算する際にゼロとみなす特異値のcutoff

実数

1e-12

convergence_epsilon

CTMの収束判定値

実数

1e-6

iteration_max

CTMの収束iterationの最大回数

整数

100

projector_corner

CTMのprojector計算で1/4角のテンソルのみを使う

真偽値

true

use_rsvd

SVD を 乱択SVD で置き換えるかどうか

真偽値

false

rsvd_oversampling_factor

乱択SVD 中に計算する特異値の数の、最終的に用いる数に対する比率

実数

2.0

meanfield_env

CTM ではなく simple update で得られる平均場環境を用いる

真偽値

false

乱拓SVDを用いたテンソル繰り込み群の手法については、 S. Morita, R. Igarashi, H.-H. Zhao, and N. Kawashima, Phys. Rev. E 97, 033310 (2018) を参照してください。

parameter.random

疑似乱数生成器に関するパラメータ

名前

説明

型

デフォルト

seed

テンソルの初期化や乱択SVD に用いる疑似乱数生成器のシード

整数

11

MPI 並列において、各プロセスは seed にプロセス番号を足した数を実際のシードとして持ちます。

例

[parameter]
[parameter.general]
is_real = true
[parameter.simple_update]
num_step = 100
tau = 0.01
[parameter.full_update]
num_step = 0  # No full update
tau = 0.01
[parameter.ctm]
iteration_max = 10
dimension = 9 # CHI

5.2.4. correlation セクション

tenes_simple では相関関数 C = <A(0)B(r)> はデフォルトでは計算されません。 相関関数を計算したい場合は、 tenes の入力ファイルで指定する correlation セクションと共通のフォーマットで指定することができます。詳細は、tenes の入力ファイル の correlation セクションをご覧ください。

5.2.5. correlation_length セクション

tenes_simple では使われず、 tenes_std の入力ファイルとしてそのままコピーされます。

相関長 \(\xi\) の計算に関する情報を指定するセクションです。

名前

説明

型

デフォルト

measure

相関長を測るかどうか

真偽値

false

num_eigvals

計算する転送行列の固有値の数

整数

4

maxdim_dense_eigensolver

密行列の対角化手法を用いる最大行列サイズ

整数

200

arnoldi_maxdim

Arnoldi 法で生成する Hessenberg 行列の次元

整数

50

arnoldi_restartdim

Arnoldi 法のリスタートで生成する初期ベクトルの本数

整数

20

arnoldi_maxiterations

Arnoldi 法の最大イテレーション回数

整数

1

arnoldi_rtol

Arnoldi 法で目指す相対残差

実数

1e-10

相関長は転送行列の固有値から計算されます。 行列サイズが maxdim_dense_eigensolver 以下のときには密行列対角化(?geev ルーチン)による対角化を、 そうでない場合は Implicit Restart Arnoldi (IRA)法による対角化を用いて固有値を計算します。

IRA 法では、 Arnoldi 過程によって大きさ arnoldi_maxdim のHessenberg 行列を生成し、その固有値を計算します。 収束していない場合は、新たに arnoldi_restartdim 本の初期ベクトルを作成し、 Arnodi 過程をやり直します (restart)。 転送行列の場合は、多くの場合で restart をする必要はありません (arnoldi_maxiterations = 1)。