4.3. DSQSS/DLA によるスピン鎖の帯磁率計算

このチュートリアルでは, 局在スピンの大きさが \(S=1/2, 1\) である2種類の 反強磁性ハイゼンベルグ鎖 (\(J=-1, L=30\)) において, 温度 \(T\) を \(0.05\) から \(2.0\) まで動かしたときの 帯磁率変化を計算します.

次に示すのは, 入力ファイルの生成と本計算を自動で行い, 帯磁率の温度依存性をファイルに書き出す Pythonスクリプトです(sample/dla/02_spinchain/exec.py).

import sys
import os.path
import subprocess

bindir = sys.argv[1] if len(sys.argv) > 1 else ''

name = 'xmzu'
Ms = [1,2]
Ts = [0.05, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0, 1.25, 1.5, 1.75, 2.0]

for M in Ms:
    output = open('{}_{}.dat'.format(name,M), 'w')
    for i,T in enumerate(Ts):
        with open('std_{}_{}.in'.format(M,i), 'w') as f:
            f.write('''
    solver = DLA
    model_type = spin
    J = -1
    F = 0.0
    lattice_type = square
    D = 1
    L = 30
    nset = 5
    ntherm = 1000
    ndecor = 1000
    nmcs = 1000
    ''')
            f.write('M = {}\n'.format(M))
            f.write('beta = {}\n'.format(1.0/T))
            f.write('outfile = res_{}_{}.dat\n'.format(M,i))
        cmd = [os.path.join(bindir, 'dsqss_pre.py'),
               '-p', 'param_{}_{}.in'.format(M,i),
               '-i', 'std_{}_{}.in'.format(M,i)]
        subprocess.call(cmd)
        cmd = [os.path.join(bindir, 'dla_H'), 'param_{}_{}.in'.format(M,i)]
        subprocess.call(cmd)
        with open('res_{}_{}.dat'.format(M,i)) as f:
            for line in f:
                if not line.startswith('R'):
                    continue
                words = line.split()
                if words[1] == name:
                    output.write('{} {} {}\n'.format(T, words[3], words[4]))

環境変数 $DSQSS_ROOT が設定されているならばそのまま実行できますが, そうでない場合は実行ファイルがインストールされているディレクトリを引数として渡します.

$ python exec.py $DSQSS_ROOT/bin

\(S=1/2\) の結果が xmzu_1.dat に, \(S=1\) の結果が xmzu_2.dat にそれぞれ書き出されます (図 4.1). スピンの大きさによって, スピンギャップの有無が異なり, その結果として絶対零度付近での帯磁率の振る舞いが異なってくることがわかります.

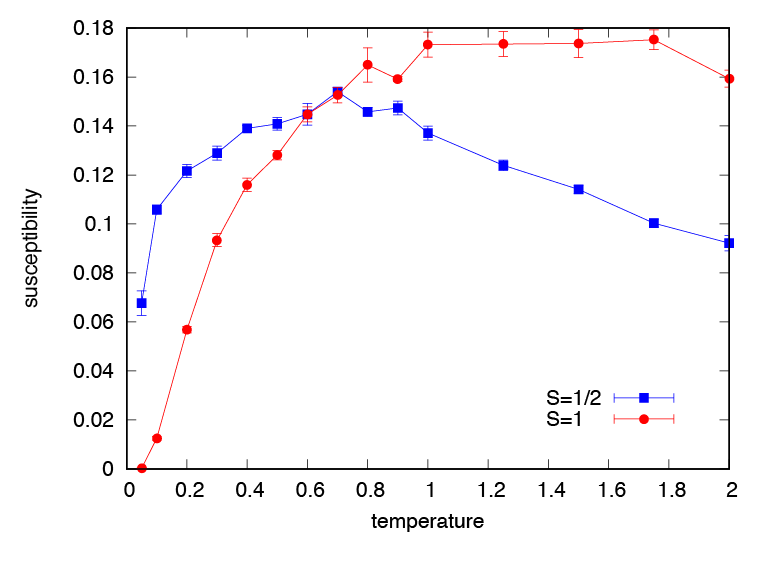
図 4.1 反強磁性ハイゼンベルグスピン鎖の帯磁率の温度依存性. 青が \(S=1/2\) で 赤が \(S=1\) の結果.