4.2. 横磁場イジング模型の実時間発展

ここでは正方格子のイジングモデルに対して、横磁場 hx をかけた場合の実時間発展の計算例について紹介します。 ハミルトニアンは

\[\begin{aligned} H = J^z \sum_{\langle i,j \rangle} {S}_i^{z} {S}_j^{z} - h^x \sum_i S_i^x \end{aligned}\]

です。 大きさ1/2のスピン演算子を用いて定義しており、パウリ演算子を直接用いたモデルと係数が異なることに注意してください。 このチュートリアルで使用する入力ファイルおよびスクリプトファイルは sample/02_time_evolution に格納されています。

最初に初期状態として、基底状態の計算を行います (simple.toml ファイル)。ここでは、

[parameter]
[parameter.general]
output = "output"
tensor_save = "save_tensor"

[parameter.simple_update]
num_step = 10
tau = 0.01

[parameter.full_update]
num_step = 0
tau = 0.0

[parameter.ctm]
meanfield_env = true
iteration_max = 10
dimension = 10

[lattice]
type = "square lattice"
L = 2
W = 2
virtual_dim = 3
initial = "ferro"

[model]
type = "spin"
Jz = -1.0
Jx = 0.0
Jy = 0.0
hx = 0.0

とします(Jz = -1.0 なので、 基底状態は強磁性状態になります)。 初期状態として基底状態を使用するため、 tensor_save = "save_tensor" として、基底状態のテンソルを保存しておきます。

次に、実時間発展を行うための入力ファイルを用意します。 実時間発展は mode を time にすることで行うことができます。 以下、入力ファイル例です( simple_te_strong.toml ファイル)。

[parameter]
[parameter.general]
output = "output_te_strong"
tensor_load = "save_tensor"
mode = "time"

[parameter.simple_update]
num_step = 500
tau = 0.01

[parameter.full_update]
num_step = 0
tau = 0.0

[parameter.ctm]
meanfield_env = true
iteration_max = 10
dimension = 10

[lattice]
type = "square lattice"
L = 2
W = 2
virtual_dim = 3
initial = "ferro"

[model]
type = "spin"
Jz = -1.0
Jx = 0.0
Jy = 0.0
hx = 2.0

ここでは、横磁場を hx = 2.0 、実時間発展の刻み幅を tau = 0.01 として時間発展させています。 また、初期状態として先ほどの基底状態を用いるため、 tensor_load = "save_tensor" として、基底状態のテンソルを読み込みます。 シンプルモードの入力ファイルを準備したあとは、基底状態計算と同様に、 tenes_simple, tenes_std, tenes を順番に実行します。 計算結果は output_te_strong ディレクトリに保存されます。 基本的に基底状態の出力と同様ですが、1列目に時間が追加されています。 たとえば FT_density.dat には物理量の期待値が時間ごとに記録されており、

# The meaning of each column is the following:
# $1: time
# $2: observable ID
# $3: real
# $4: imag
# The meaning of observable IDs are the following:
# 0: Energy
# 1: Sz
# 2: Sx
# 3: Sy
# 4: bond_hamiltonian
# 5: SzSz
# 6: SxSx
# 7: SySy

0.00000000000000000e+00 0 -5.00184764052080899e-01  0.00000000000000000e+00
0.00000000000000000e+00 1  4.99999945646528332e-01  0.00000000000000000e+00
0.00000000000000000e+00 2  9.24306486797199186e-05  0.00000000000000000e+00
0.00000000000000000e+00 3  2.34088935337348195e-06  0.00000000000000000e+00
0.00000000000000000e+00 4 -5.00184764052080899e-01  3.47535331983321418e-21
0.00000000000000000e+00 5  4.99999902788251294e-01 -8.46256269499545126e-22
0.00000000000000000e+00 6  1.12653588020163689e-05  6.35907290717320676e-22
0.00000000000000000e+00 7 -1.12840199341671039e-05 -2.06527532941704114e-21

のようになっています。 2列目は物理量の種類を表しており、この計算では1番が縦磁化 \(m^z = \langle S^z \rangle\) です。 awk などでフィルタリングすることで、特定の物理量の時間発展を取り出せます。

awk '$2 == 1 {print $1, $3, $4}' output_te_strong/TE_density.dat > magnetization_strong.dat

時間発展の様子をいくつかの横磁場で見るために、 simple_te_middle.toml (hx = 0.8)、 simple_te_weak.toml (hx = 0.5) という入力ファイルもサンプルとして用意しています。 また、これらを一括して計算するためのスクリプト run.sh も準備しています。 あらかじめ tenes などにパスを通した上で

sh run.sh

により計算を実行します。数十秒で計算が終わります。 計算が終了したら、gnuplotを起動し、

load 'plot.plt'

とすれば、 磁化 \(m^z\) の時間発展の様子がプロットされます。 その結果を 図 4.2 に示します。

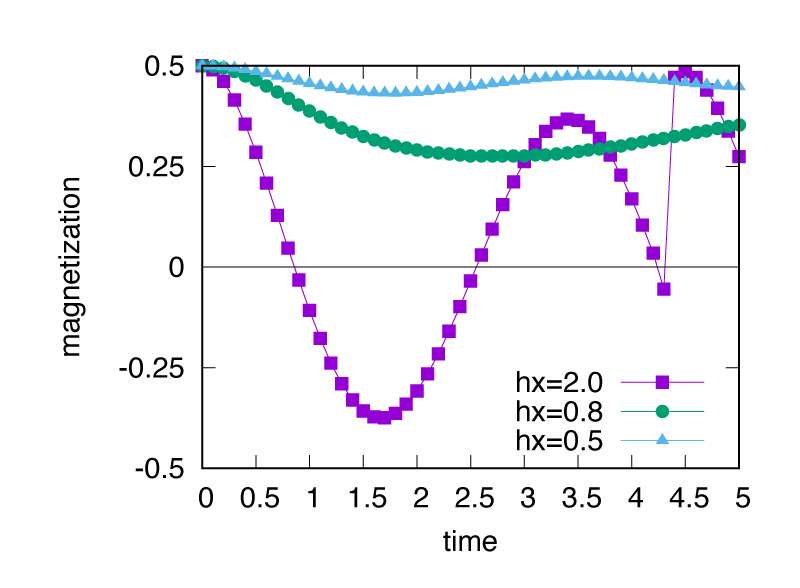
図 4.2 イジング模型の実時間発展の図. 縦軸は磁化、横軸は時間を表す。

横磁場を強くしていくと磁化の振動が大きくなり、量子相転移点を超えると \(m^z = 0\) を超えて振動するようになります [DQPT] 。

なお、時間発展が進むにつれてエンタングルメントが大きくなり、ある時点でテンソルネットワークの容量が波動関数を表現するのに足りなくなります。 今の場合、 hx=2.0 における t=4.25 のジャンプがこの問題を示しています。 実際に使用する場合には、このような不連続性が存在しないかを確認の上、ジャンプが存在する場合にはテンソルネットワークの容量が足りなくならないように、 virtual_dimension を大きくするなどの対策を行う必要があります。 例えば、 virtual_dimension = 10 に変更して上述の計算を行うと、 図 4.3 に示すように不連続性が消えることがわかります。

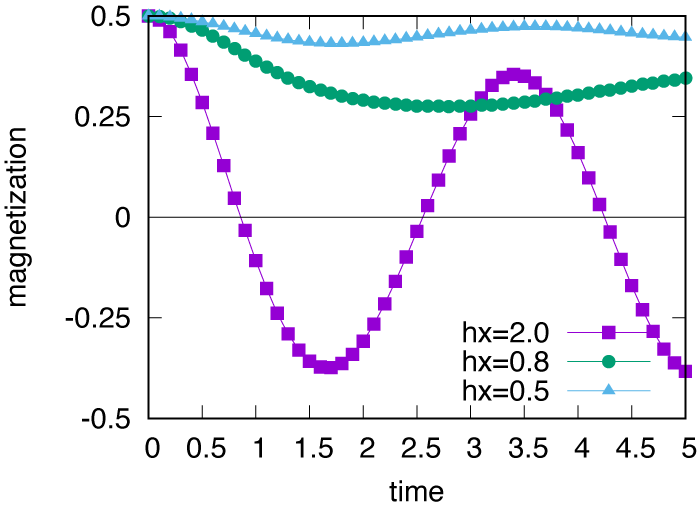
図 4.3 イジング模型の実時間発展の図. 縦軸は磁化、横軸は時間を表す。 virtual_dimension = 10 とした場合の結果。

参考文献

[DQPT] M. Heyl, A. polkovnikov, and S. Kehrein, Dynamical Quantum Phase Transitions in the Transverse-Field Ising Model, Phys. Rev. Lett. 110, 135704 (2013). link