4.6. スタンダードモードによる格子・模型・演算子の定義

スタンダードモードを使うとユーザが独自に格子・模型・演算子を定義できます。 ここではスタンダードモードの使い方を説明します。

4.6.1. ユニットセルの定義

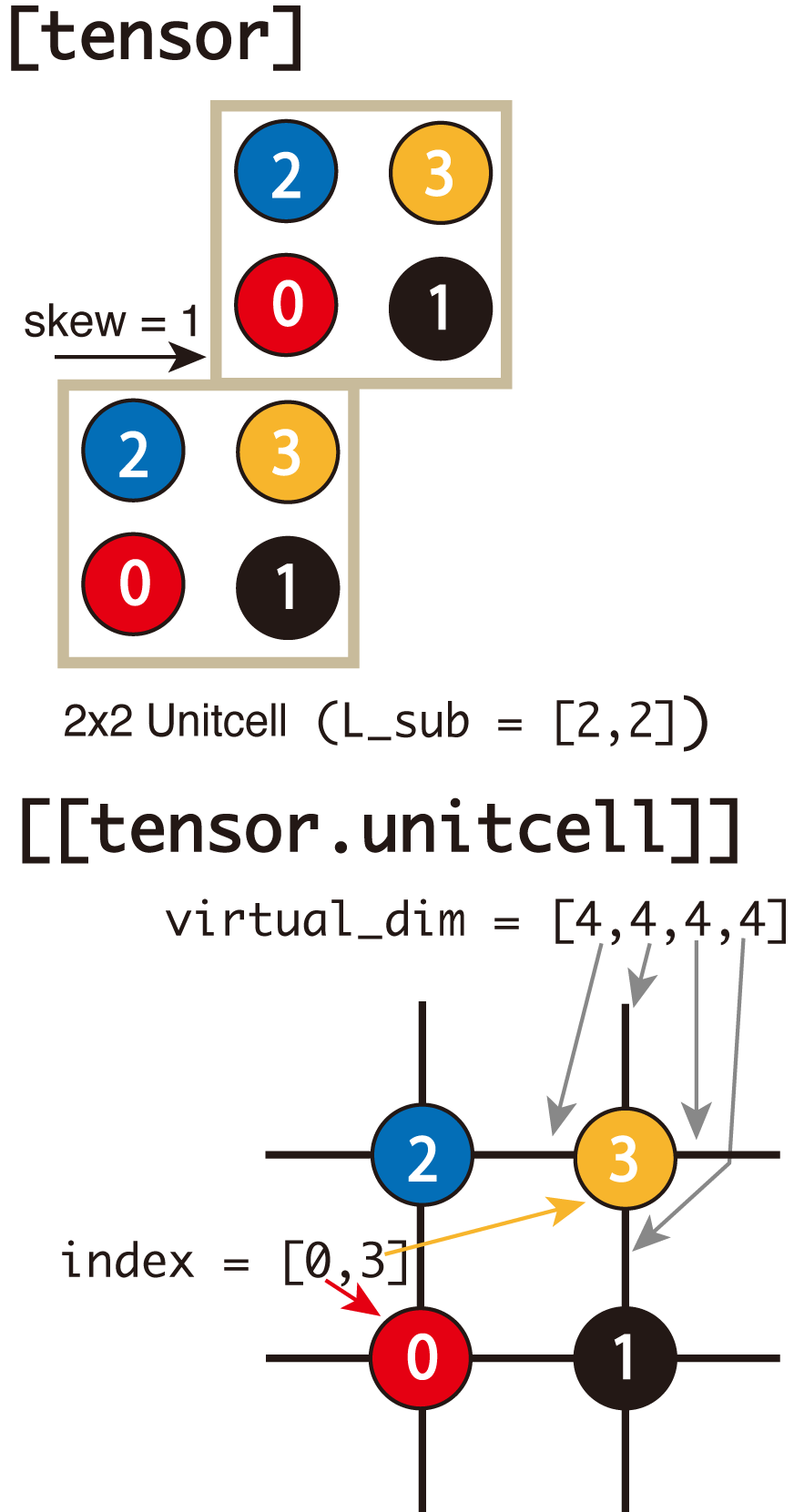
図 4.8 [tensor] と [[tensor.unitcell]]

ユニットセルの定義は [tensor] と [[tensor.unitcell]] を用います

[tensor]                # どういう格子を定義したか？
L_sub = [2, 2]          # 2x2 unitcell
skew = 0                # y方向の境界を越えた時のx方向のずれ

[[tensor.unitcell]]
virtual_dim = [4, 4, 4, 4] # ボンド次元 (←,↑,→,↓の順)
index = [0, 3]             # ユニットセル中のどのテンソルかを示す番号
physical_dim = 2           # 物理ボンドの次元
initial_state = [1.0, 0.0] # 初期状態の係数
noise = 0.01               # 初期テンソルのゆらぎ

全体の初期状態 \(\ket{\psi}\) はサイトごとの初期状態 \(\ket{\psi_i}\) の直積状態 \(\ket{\Psi} = \otimes_i \ket{\Psi_i}\) で書けます。 \(\ket{\psi_i}\) は、initial_state配列の要素を前から \(a_0,a_1,\ldots,a_{d-1}\) とすると、

\[\ket{\Psi_i} \propto \sum_k^{d-1}a_k\ket{k}\]

と書けます。

4.6.2. 模型（ハミルトニアン）の定義

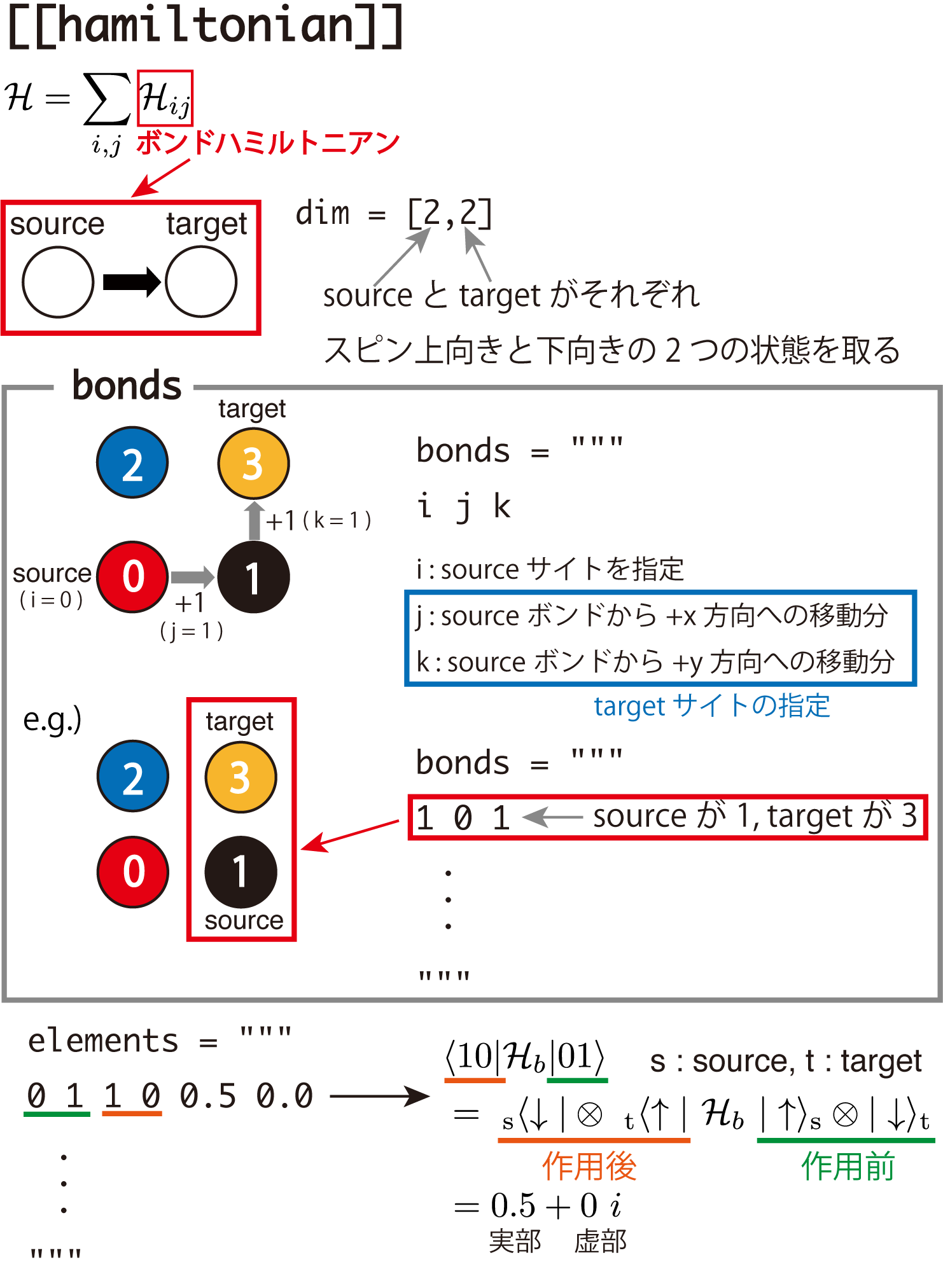
図 4.9 [[hamiltonian]] の模式図

TeNeSはハミルトニアンをボンドハミルトニアン (2サイトハミルトニアン) とサイトハミルトニアン（1サイトハミルトニアン）の和として扱います。

\[\mathcal{H} = \sum_{i,j}\mathcal{H}_{i,j} + \sum_{i}\mathcal{H}_{i}\]

これら局所ハミルトニアンは（非ゼロの）行列要素と作用するサイト・ボンドの組み合わせで定義されます。 ボンドはsourceサイトとtargetサイトの組であると考えます。 行列要素によって模型が、ボンドによって格子が定義されます。

ボンドハミルトニアン

それぞれの局所ハミルトニアンは [[hamiltonian]] で記述されます。 ボンドハミルトニアンの作用するボンドは bonds 文字列で指定します。

[[hamiltonian]]
bonds = """  # 作用するボンドの集合(1行1ボンド)
0 1 0        # 1列目: ユニットセル内のsourceの番号
1 1 0        # 2列目: sourceからみたtargetのx座標(変位)
2 1 0        # 3列目: sourceからみたtargetのy座標(変位)
3 1 0
0 0 1
1 0 1
2 0 1
3 0 1
"""

3つの整数からなる 1行が1つのボンドを表現します。 最初の整数はユニットセル内の source サイトの番号です。 残り2つは、 source サイトから見た target サイトの x 座標、 y 座標です。 たとえば 0 1 0 は 0番と右隣 (x+=1, y+=0) にある1番の組、 1 0 1 は1番と上隣 (x+=0, y+=1) にある3番の組を表します。

ボンドハミルトニアンの次元、すなわち作用するサイト対の取りうる状態数の数は dim で指定し、 ボンドハミルトニアン演算子の非ゼロ行列要素は elements 文字列で指定します。

dim = [2, 2]       # [source, target] の取りうる状態数の対
elements = """     # ハミルトニアンの(非ゼロな)行列要素(1行1要素)
0 0 0 0 0.25 0.0   # 1列目: 作用前のsourceの状態
1 0 1 0 -0.25 0.0  # 2列目: 作用前のtargetの状態
0 1 1 0 0.5 0.0    # 3列目: 作用後のsourceの状態
1 0 0 1 0.5 0.0    # 4列目: 作用後のtargetの状態
0 1 0 1 -0.25 0.0  # 5列目: 要素の実部
1 1 1 1 0.25 0.0   # 6列目: 要素の虚部
"""

elements の1行が行列要素1つに対応します。 最初の整数2つは演算子作用 前 の2サイトそれぞれ (source, target) の状態、 つづく整数2つは演算子作用 後 の2サイトそれぞれ (source, target) の状態を示し、 残る2つの数値は行列要素の実部と虚部を表します。

サイトハミルトニアン

サイトハミルトニアンは作用するサイトと（非ゼロ）行列要素との組み合わせで定義します。:

[[hamiltonian]]
dim = [2]
sites = []
elements = """
1 0 -0.5 0.0
0 1 -0.5 0.0
"""

サイトは sites で指定します。空リストはすべてのサイトを意味します。

行列要素 elements の指定方法はボンドハミルトニアンと同様です（作用するサイトが1つであることに留意）。

4.6.3. 演算子の定義

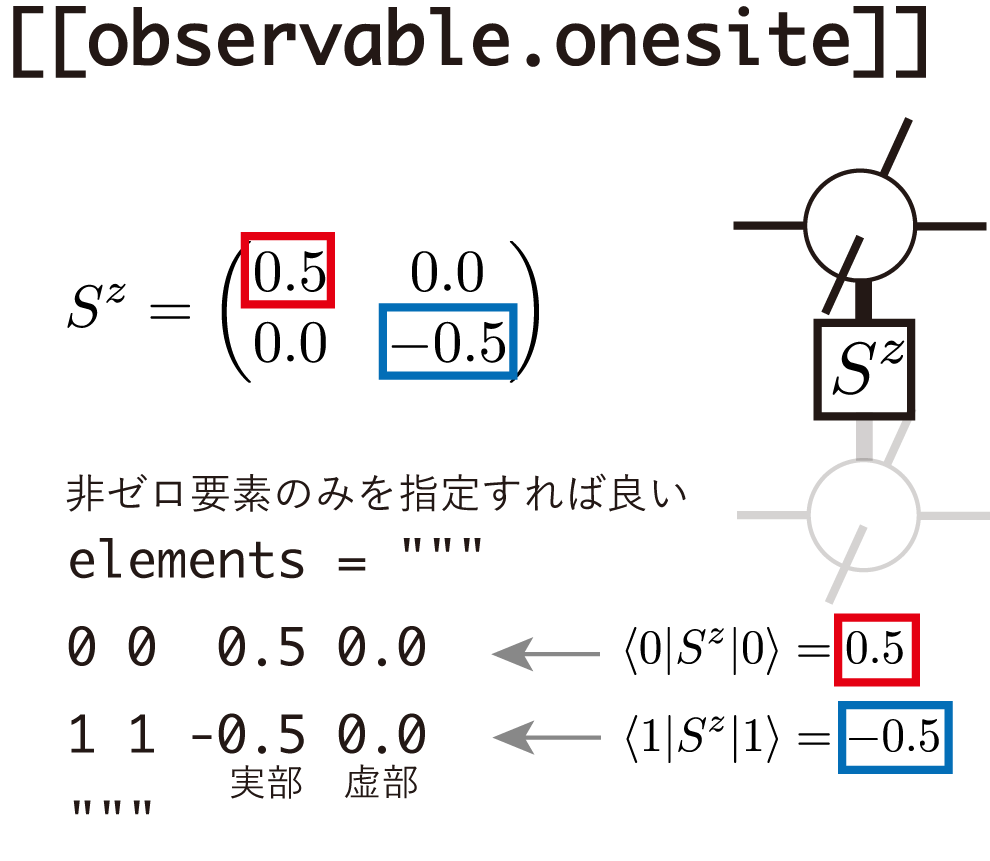
図 4.10 [[observable.onesite]]

最終的に期待値を計算する演算子は [observable] 以下に定義します。 現在は1サイト演算子と2サイト演算子が計算可能です。

定義の仕方はハミルトニアンと同様ですが、名前 name と演算子番号 group が必要です。 演算子番号は1サイト演算子と2サイト演算子とで別あつかいです。 なお、エネルギー演算子（ハミルトニアン）もあらためて [observable] に定義する必要があります (0 番の演算子が定義されていない時、 tenes_std は [[hamiltonian]] の内容を自動でコピーします)。

1サイト演算子の例として、スピンのz 成分

\[\begin{split}S^z = \begin{pmatrix} 0.5 & 0.0 \\ 0.0 & -0.5 \\ \end{pmatrix}\end{split}\]

を考えると、これは次のように表現できます

[[observable.onesite]] # 1サイト演算子
name = "Sz"     # 名前
group = 0       # 1サイト演算子の識別番号
sites = []      # 1サイト演算子が作用するサイトの番号 ([]はすべてを意味する)
dim = 2         # 1サイト演算子の次元
elements = """  # 1サイト演算子行列の非ゼロ要素 (1行1要素)
0 0 0.5 0.0     # 1,2列目: 作用前後の状態
1 1 -0.5 0.0    # 3,4列目: 要素の実部・虚部
"""

2サイト演算子の例として、最近接ボンドにおける Sz 相関 \(S^z_i S^z_j\) を例に取ると

[[observable].twosite]] # 2サイト演算子
name = "SzSz" # 名前
group = 1 # 2サイト演算子の識別番号 (1サイトとは独立)
dim = [2, 2] # 次元
bonds = """ # 作用するボンド (サイト対)
0 1 0
1 1 0
2 1 0
3 1 0
0 0 1
1 0 1
2 0 1
3 0 1
"""
ops = [0, 0] # 1サイト演算子の直積で書ける場合、その識別番号
             # 今回は"Sz"が0番の1サイト演算子
             # elementsとして行列要素を陽に書くことも可能
             # (ボンドハミルトニアンと同じ書式)

となります。 ボンドの指定方法はボンドハミルトニアンと同様です。 行列要素についても、ボンドハミルトニアンと同様に elements で指定することもできますが、 この例のように、 1サイト演算子の直積で書ける場合には、 ops を用いてその識別番号で表すこともできます。

4.6.4. 例： 交代磁場中の反強磁性ハイゼンベルグ模型

自分でハミルトニアンを書く例として、交代磁場中の正方格子反強磁性ハイゼンベルグ模型を考えます。 ハミルトニアンは

\[\mathcal{H} = J \sum_{\braket{ij}} S_i \cdot S_j - h \sum_{i \in A} S_i^z + h \sum_{j \in B} S_j^z\]

です。 ここで、 \(\sum_{\braket{ij}}\) は最近接サイト対に対する和で、 \(A, B\) はそれぞれ正方格子の副格子を表します。 ボンドハミルトニアン \(\mathcal{H}_ij\) は

\[\begin{split}\begin{split} \mathcal{H}_{ij} &= J S_i \cdot S_j \\ &= \begin{pmatrix} J/4 & 0 & 0 & 0 \\ 0 & -J/4 & J/2 & 0 \\ 0 & J/2 & -J/4 & 0 \\ 0 & 0 & 0 & J/4 \\ \end{pmatrix} \end{split}\end{split}\]

で、サイトハミルトニアン \(\mathcal{H}_i\) は

\[\begin{split}\begin{split} \mathcal{H}_{i} &= -h S_i^z \\ &= \begin{pmatrix} -h/2 & 0 \\ 0 & h/2 \\ \end{pmatrix} \end{split}\end{split}\]

です。 たとえば、極端な例として \(J = 0, h = 1\) を考えてみると、 入力ファイル (sample/06_std_model/std.toml) は次のとおりです。

[parameter]
[parameter.general]
is_real = true
tensor_save = "tensor"
[parameter.simple_update]
num_step = 1000
tau = 0.01
[parameter.full_update]
num_step = 0
tau = 0.01
[parameter.ctm]
iteration_max = 10
dimension = 10

[tensor]
type = "square lattice"
L_sub = [2, 2]
skew = 0

[[tensor.unitcell]]
virtual_dim = [2, 2, 2, 2]
index = [0, 3]
physical_dim = 2
initial_state = [1.0, 0.0]
noise = 0.01

[[tensor.unitcell]]
virtual_dim = [2, 2, 2, 2]
index = [1, 2]
physical_dim = 2
initial_state = [0.0, 1.0]
noise = 0.01

[[hamiltonian]]
dim = [2]
sites = [0, 3]
elements = """
0 0 -0.5 0.0
1 1 0.5 0.0
"""

[[hamiltonian]]
dim = [2]
sites = [1, 2]
elements = """
0 0 0.5 0.0
1 1 -0.5 0.0
"""

[observable]
[[observable.onesite]]
name = "Sz"
group = 1
sites = []
dim = 2
elements = """
0 0 0.5 0.0
1 1 -0.5 0.0
"""

[[observable.twosite]]
name = "SzSz"
group = 1
dim = [2, 2]
bonds = """
0 1 0
1 1 0
2 1 0
3 1 0
0 0 1
1 0 1
2 0 1
3 0 1
"""
ops = [1, 1]

これを用いて計算すると

$ tenes_std std.toml
$ tenes input.toml

   ... skipped ...

Onesite observables per site:
  hamiltonian = -0.5 0
  Sz          = 0 0
Twosite observables per site:
  SzSz        = -0.5 0

   ... skipped

となります。 とくに1サイト演算子の期待値 output/onesite_obs.dat は:

# $1: op_group
# $2: site_index
# $3: real
# $4: imag

0 0 -5.00000000000000000e-01 0.00000000000000000e+00
0 1 -5.00000000000000000e-01 0.00000000000000000e+00
0 2 -5.00000000000000000e-01 0.00000000000000000e+00
0 3 -5.00000000000000000e-01 0.00000000000000000e+00
1 0 5.00000000000000000e-01 0.00000000000000000e+00
1 1 -5.00000000000000000e-01 0.00000000000000000e+00
1 2 -5.00000000000000000e-01 0.00000000000000000e+00
1 3 5.00000000000000000e-01 0.00000000000000000e+00
-1 0 2.20256797875764860e+04 0.00000000000000000e+00
-1 1 2.20198975366861232e+04 0.00000000000000000e+00
-1 2 2.20294461413457539e+04 0.00000000000000000e+00
-1 3 2.20236290136460302e+04 0.00000000000000000e+00

であり、 \(S^z\) (op_group=1)を見ると A 副格子 (site_index=0,3) のスピンは上 (0.5) を、 B 副格子 (site_index=1,2) のスピンは下 (-0.5) を向いていることがわかります。 今回は交代磁場のみをかける (\(J = 0, h = 1\)) ことで、Neel 状態を表すようなテンソルを得られました。 このテンソルは tensor ディレクトリに保存されており (tensor_save = "tensor")、そのまま他の模型での初期テンソルとして利用できます (tensor_load = "tensor" とする)。