4.3. 横磁場イジング模型の有限温度計算

ここでは正方格子の強磁性イジングモデルに対して、横磁場 hx をかけた場合の有限温度の計算例について紹介します。 ハミルトニアンは

\[\begin{aligned} H = J^z \sum_{\langle i,j \rangle} {S}_i^{z} {S}_j^{z} - h^x \sum_i S_i^x \end{aligned}\]

です。 大きさ1/2のスピン演算子を用いて定義しており、パウリ演算子を直接用いたモデルと係数が異なることに注意してください。

このチュートリアルで使用する入力ファイルおよびスクリプトファイルは sample/03_finite_temperature に格納されています。 以下が入力ファイルの例です (simple_ft_strong.toml ファイル)。ここでは、

[parameter]
[parameter.general]
mode = "finite"
is_real = false
output = "output_ft_strong"
measure_interval = [10, 10, 5]

[parameter.simple_update]
num_step = [50, 200, 10]
tau = [0.01, 0.005, 0.05]

[parameter.full_update]
num_step = 0
tau = 0.0

[parameter.ctm]
iteration_max = 10
dimension = 10

[lattice]
type = "square lattice"
L = 2
W = 2
virtual_dim = 3

[model]
type = "spin"
Jz = -1.0
Jx = 0.0
Jy = 0.0
hx = 2.0

とします。 実時間発展は parameter.general セクションの mode を finite にすることで行うことができます。 横磁場を hx = 2.0 、 tau = 0.01 (逆温度の刻み幅は 2 tau)として有限温度計算をしています。 シンプルモードの入力ファイルを用意したら、基底状態計算などと同様に、 tenes_simple, tenes_std, tenes コマンドを用いて計算を実行します。 計算結果は output_ft_strong ディレクトリ以下に出力されます。基本的に基底状態計算の出力と同様ですが、1列目に逆温度が追加されています。 例えば FT_density.dat は

# The meaning of each column is the following:
# $1: inverse temperature
# $2: observable ID
# $3: real
# $4: imag
# The meaning of observable IDs are the following:
# 0: Energy
# 1: Sz
# 2: Sx
# 3: Sy
# 4: bond_hamiltonian
# 5: SzSz
# 6: SxSx
# 7: SySy

0.00000000000000000e+00 0  0.00000000000000000e+00  0.00000000000000000e+00
0.00000000000000000e+00 1  0.00000000000000000e+00  0.00000000000000000e+00
0.00000000000000000e+00 2  0.00000000000000000e+00  0.00000000000000000e+00
0.00000000000000000e+00 3  0.00000000000000000e+00  0.00000000000000000e+00
0.00000000000000000e+00 4  0.00000000000000000e+00  0.00000000000000000e+00
0.00000000000000000e+00 5  0.00000000000000000e+00  0.00000000000000000e+00
0.00000000000000000e+00 6  0.00000000000000000e+00  0.00000000000000000e+00
0.00000000000000000e+00 7  0.00000000000000000e+00  0.00000000000000000e+00

   ... continued ...

となっています。 2列目が物理量の種類を示しており、例えば0はエネルギーなので、 awk などでエネルギーだけを取り出すことで温度依存性を調べられます:

awk '$2 == 0 {print $1, $3, $4}' output_ft_strong/FT_density.dat > energy_strong.dat

有限温度の振る舞いをいくつかの横磁場で見るために、 simple_ft_middle.toml (hx = 0.8)、 simple_te_weak.toml (hx = 0.5)、 simple_ft_zero.toml (hx = 0.0) という入力ファイルもサンプルとして用意しています。 また、これらを一括して計算し、エネルギー・縦磁化・横磁化を保存するスクリプト run.sh も準備しています。 あらかじめ tenes などにパスを通した上で

sh run.sh

により計算を実行します。1分程度で計算が終わります。 比熱は直接計算するのが難しいため、エネルギーの温度微分として計算します。 calcspec.py はエネルギーをスプライン補間して温度微分することで比熱を計算します。:

python3 calcspec.py

計算結果を可視化するため、エネルギー、比熱、磁化を表示するためのスクリプト plot_e.plt 、 plot_c.plt、 plot_mx.plt 、 plot_mz.plt を用意しています。

gnuplot -persist plot_e.plt
gnuplot -persist plot_c.plt
gnuplot -persist plot_mx.plt
gnuplot -persist plot_mz.plt

その結果を 図 4.4 に示します。 比較のため、量子モンテカルロ法を用いて計算した結果も一緒に表示しています ( ALPS/looper を使用)。

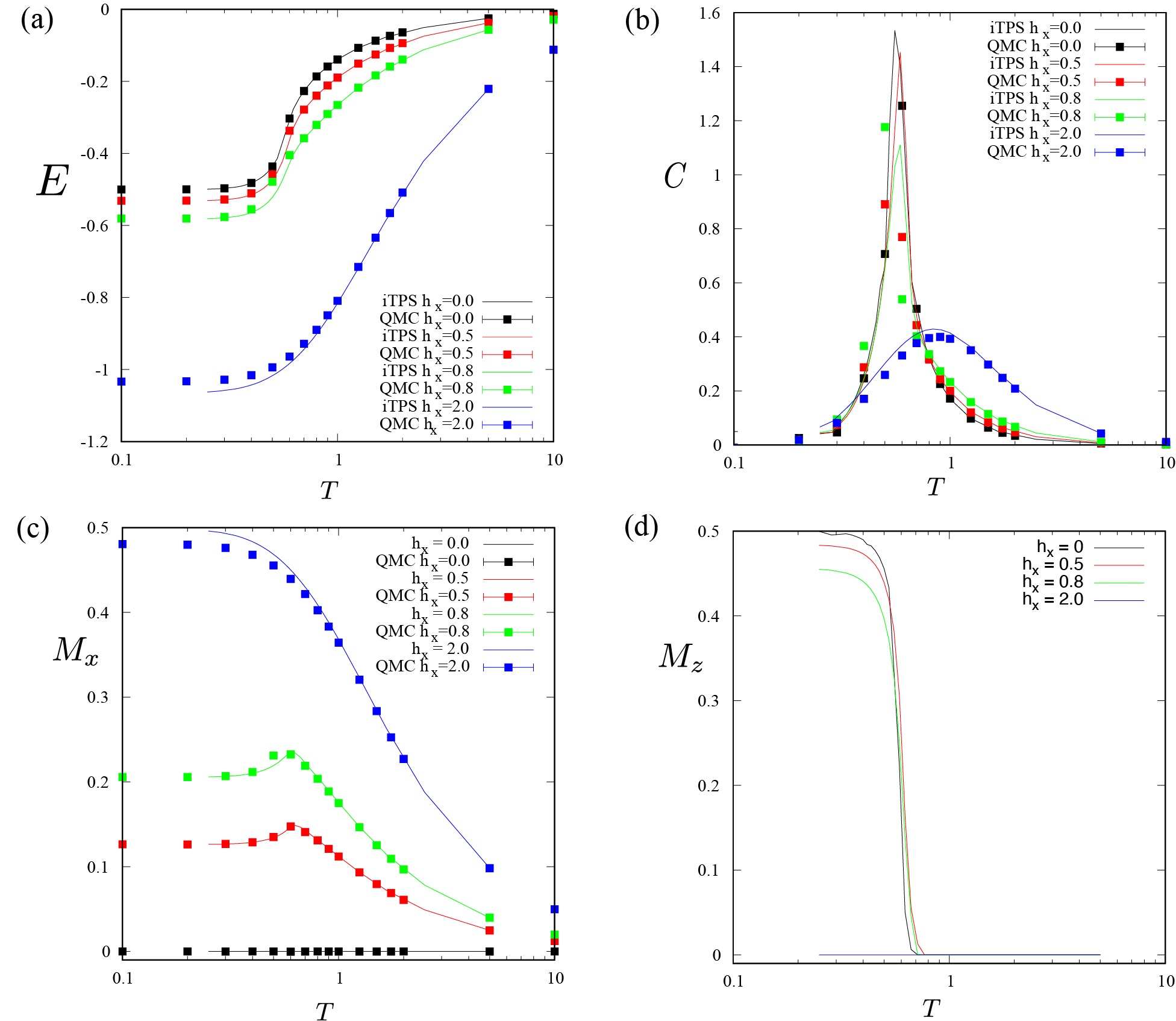
図 4.4 イジング模型の有限温度計算の図: (a) エネルギー、(b) 比熱、(c) \(m_x\) 、(d) \(m_z\). 縦軸は物理量、横軸は温度を表す。