4.5. 三角格子上のハードコアボゾン模型の相図

最後に三角格子上で定義されたハードコアボゾン模型の絶対零度のおける相図の計算を紹介します。 模型のハミルトニアンは以下のようになります:

\[\begin{aligned} H = \sum_{\langle i,j \rangle} \Bigl[ -t (b_i^\dagger b_j + b_j^\dagger b_i) + V n_i n_j \Bigr] -\mu \sum_i n_i \end{aligned}\]

ここで\(\langle i, j\rangle\)は隣接サイトの組を表し、\(\mu\)は化学ポテンシャル、\(t\)はホッピングエネルギー、\(V\)は隣接サイト間の相互作用の大きさを表します。 ハードコアボゾン模型では、各サイトのボソン数は0か1に制限されます。 この模型では、2つのタイプの長距離秩序によって特徴づけられるいくつかの秩序相が現れることが知られています [Wessel] 。 まずは消滅演算子の期待値の大きさ\(|\langle b \rangle|\)で特徴づけられる超流動秩序です。 もうひとつは固体秩序です。 1/3フィリングでは、 図 4.7 の挿入図に示すような\(\sqrt{3}\times\sqrt{3}\)超格子構造をもつ固体相が出現します。 これは波数\(\boldsymbol{Q}=(4\pi/3,0)\)の構造因子\(S(\boldsymbol{Q}) = \sum_{ij}^{N_\text{sites}} \langle n_i n_j \rangle \exp[-i\boldsymbol{Q}\cdot(r_i - r_j)] / N_\text{site}\)を計算することで特徴づけることができます。

この模型の計算を行うには、 sample/05_hardcore_boson_triangular ディレクトリ中にある toml ファイル basic.toml, nn_obs.toml と、Pythonスクリプト run.py を利用します。 basic.toml ファイルには模型の設定やパラメータなどが記述されています。このファイルの記述は、前節の三角格子ハイゼンベルク模型とほぼ同じであるため、内容は割愛します。唯一の変更点は最後の model セクションだけです。ここで、 type = "boson" によってハードコアボゾン模型を指定しており、 t = 0.1, V = 1 によってホッピングおよび隣接サイト間相互作用の大きさを指定しています。

構造因子 \(S(\boldsymbol{Q})\) を計算するためには、（ユニットセル中の）全サイト対における密度密度相関 \(\langle n_i n_j \rangle\) を計算する必要があります。 この演算子は tenes_simple では定義されないため、別途定義する必要があります。 nn_obs.toml ファイルに \(3 \times 3\) ユニットセルにおける演算子が定義されており、 run.py で tenes_std の入力ファイル std_XXX_YYY.toml に追記しています。

より大きなユニットセルを用いる場合には、密度密度相関を計算するコストが非常に大きくなってしまい、構造因子を計算することが現実的ではなくなります。 一方、TeNeSは（正方格子iTPSの）x軸、y軸方向の相関関数を低コストで計算できます。これを利用して長距離秩序の有無を確認できます。 また、1体の密度演算子の期待値 \(\langle n_i \rangle\) のフーリエ変換 \(n(\boldsymbol{Q})\) も使えます。 1/3フィリングの基底状態は3重縮退していますが、有限ボンド次元計算ではそのうちのどれかが選ばれます。その結果、得られる密度はサイト依存性があります。

実際にスクリプト run.py を使って計算を実行してみましょう。 あらかじめ tenes などにパスを通した上で

python run.py

により計算を実行します。数分〜十数分程度で計算が終わります。 計算が終了したら、gnuplotを起動し、

load 'plot.gp'

とすれば、 図 4.7 のようなグラフが得られます。 \(S(\boldsymbol{Q})\) がユニットセル内の密度相関関数から計算した構造因子、 \(S'(\boldsymbol{Q})\) がx方向の相関関数から計算した構造因子、 \(n(\boldsymbol{Q})\) が密度のフーリエ変換、 \((|\langle b \rangle| + |\langle b^\dagger \rangle|)/2\) が超流動秩序パラメータです。 なお、ここで計算に用いたボンド次元は小さい(ボンド次元2)ため、計算精度はそれほど高くありません。 スクリプト run.py の冒頭でボンド次元を増やすことで、時間がかかりますが、より高精度の計算を行うこともできます。 この図から、系の基底状態は3種類の相、つまり(a) 超流動相(\(-0.5 \lesssim \mu/V \lesssim -0.2\)), (b) 固体相(\(-0.2 \lesssim \mu/V \lesssim 2.4\)), および(c) 超流動固体相(\(2.4 \lesssim \mu/V\))が現れることがわかります。これは先行研究の結果と整合します [Wessel] 。

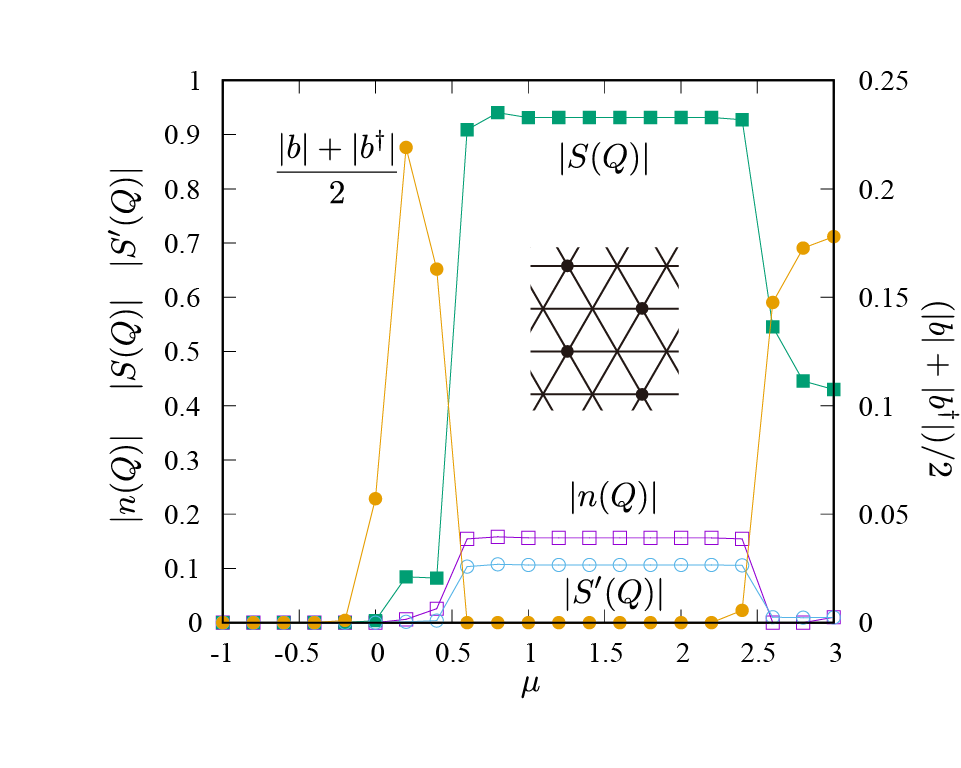
図 4.7 三角格子上のハードコアボゾン模型の基底状態相図.

参考文献

[Wessel] S. Wessel, M. Troyer, Supersolid hard-core bosonson the triangular lattice, Phys. Rev. Lett. 95, 127205 (2005). link.